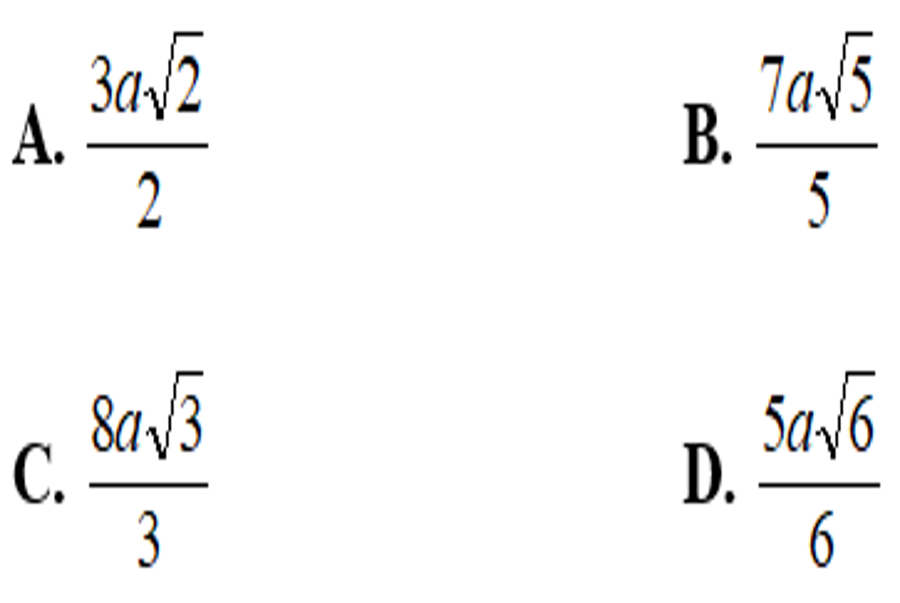Bài tập về khoảng cách từ điểm đến mặt phẳng

Các dạng bài tập Khoảng cách chọn lọc, có lời giải        Trang trước Trang sau

Phần Khoảng cách Toán lớp 11 với các dạng bài tập tinh lọc có trong Đề thi THPT Quốc gia và trên 100 bài tập trắc nghiệm tinh lọc, có giải thuật. Vào Xem cụ thể để theo dõi các dạng bài Khoảng cách hay nhất tương ứng .Nội dung chính

• Các dạng bài tập Khoảng cách chọn lọc, có lời giải        Trang trước Trang sau
• Cách tính khoảng cách từ một điểm đến một đường thẳng
• Cách tính khoảng cách từ một điểm đến một mặt phẳng
• Cách tính khoảng cách giữa đường thẳng và mặt phẳng song song
• Video liên quan

Cách tính khoảng cách từ một điểm đến một đường thẳng

– Để tính khoảng cách từ điểm M đến đường thẳng Δ ta cần xác lập được hình chiếu H của điểm M trên đường thẳng Δ. Khi đó MH chính là khoảng cách từ M đến đường thẳng. Điểm H thường được dựng theo hai cách sau :

+ Trong mp(M; Δ) vẽ MH vuông góc Δ   d(M; Δ) = MH

+ Dựng mặt phẳng ( α ) qua M và vuông góc với Δ tại H d ( M ; Δ ) = MH .- Hai công thức sau thường được dùng để tính MH :+ Tam giác AMB vuông tại M và có đường cao AH thì+ MH là đường cao của tam giác MAB thì

Ví dụ 1: Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC)  và SA = 3a. Diện tích tam giác ABC bằng 2a2; BC = a. Khoảng cách từ S đến BC bằng bao nhiêu?

A. 2 aB. 4 aC. 3 aD. 5 a

Hướng dẫn giải

+ Kẻ AH vuông góc với BCTa có : SA ( ABC ) SA BCLại có : AH BC nên BC ( SAH )SH BC và khoảng cách từ S đến BC chính là SH+ Ta có tam giác vuông SAH vuông tại A nên ta cóChọn D

Ví dụ 2: Cho hình chóp ABCD  có cạnh AC  (BCD) và BCD là tam giác đều cạnh bằng a. Biết AC = a2  và M là trung điểm của BD.  Khoảng cách từ C đến đường thẳng AM  bằng

Hướng dẫn giải

+ Do tam giác BCD đều cạnh a nên đường trung tuyến CM đồng thời là đường cao và MC = a3 / 2+ Ta có : AC ( BCD ) AC CMGọi H là chân đường vuông góc kẻ từ C đến AMTa có :Chọn đáp án C

Ví dụ 3: Cho tứ diện SABC trong đó SA; SB; SC vuông góc với nhau từng đôi một và SA = 3a; SB = a; SC = 2a. Khoảng cách từ A đến đường thẳng BC bằng:

Hướng dẫn giải

Chọn đáp án BXét trong tam giác SBC vuông tại S có SH là đường cao ta có :+ Ta dễ chứng tỏ được AB ( SBC ) SH AS SHtam giác SAH vuông tại S .Áp dụng định lsi Pytago trong tam giác ASH vuông tại S ta có :Chọn B

Cách tính khoảng cách từ một điểm đến một mặt phẳng

Để tính được khoảng từ điểm A đến mặt phẳng ( α ) thì điều quan trọng nhất là ta phải xác lập được hình chiếu của điểm A trên ( α )Cho trước SA Δ ; trong đó S ( α ) và Δ ( α )Bước 1 : Dựng AK Δ Δ ( SAK ) ( α ) ( SAK ) và ( α ) ( SAK ) = SKBước 2 : Dựng AP SK AP ( α ) d ( A, ( α ) ) = AP

Ví dụ 1: Trong mặt phẳng (P)  cho tam giác đều ABC cạnh a. Trên tia Ax vuông góc với mặt phẳng (P)  lấy điểm S  sao cho SA = a. Khoảng cách từ A  đến (SBC) bằng

Hướng dẫn giải

– Gọi M là trung điểm của BC, H là hình chiếu vuông góc của A trên SM- Ta có BC AM ( trong tam giác đều đường trung tuyến đồng thời là đường cao ). Và BC SA ( vì SA vuông góc với ( ABC ) ). Nên BC ( SAM ) BC AHMà AH SM, do đó AH ( SBC )

Chọn đáp án C

Ví dụ 2: Cho hình chóp S.ABCD có SA  (ABCD), đáy ABCD là hình chữ nhật. Biết  AD = 2a; SA = a. Khoảng cách từ A  đến (SCD)  bằng:

Hướng dẫn giải

SA ( ABCD ) nên SA CD, AD CDSuy ra ( SAD ) CDTrong ( SAD ) kẻ AH vuông góc SD tại HKhi đó AH ( SCD )Chọn đáp án C

Ví dụ 3: Hình chóp đều S.ABC có cạnh đáy bằng 3a cạnh bên bằng 2a. Khoảng cách từ S đến (ABC)  bằng :

A. 2 aB. a3 C. aD. a5

Hướng dẫn giải

+ Gọi O là trọng tâm tam giác ABC.Do tam giác ABC đều nên O là tâm đường tròn ngoại tiếp tam giác ABC+ Ta có : SA = SB = SC và OA = OB = OC nên SO là trục đường tròn ngoại tiếp tam giác ABC. Do đó SO ( ABC )Chọn đáp án C

Cách tính khoảng cách giữa đường thẳng và mặt phẳng song song

Cho đường thẳng d / / ( P ) ; để tính khoảng cách giữa d và ( P ) ta thực thi các bước :+ Bước 1 : Chọn một điểm A trên d, sao cho khoảng cách từ A đến ( P ) hoàn toàn có thể được xác lập dễ nhất .+ Bước 2 : Kết luận : d ( d ; ( P ) ) = d ( A ; ( P ) ) .

Ví dụ 1: Cho hình chóp S. ABCD có SA  (ABCD), đáy ABCD là hình thang vuông  tại A  và B;  AB = a. Gọi I và J  lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa đường thẳng IJ  và (SAD)

Hướng dẫn giải

Chọn CTa có : I và J lần lượt là trung điểm của AB và CD nên IJ là đường trung bình của hình thang ABCD

Ví dụ 2: Cho hình thang vuông ABCD vuông ở A và D; AD = 2a. Trên đường thẳng vuông góc tại D với (ABCD)  lấy điểm S với SD = a2. Tính khỏang cách giữa đường thẳng CD và (SAB).

Hướng dẫn giải

Chọn AVì DC / / AB nên DC / / ( SAB )d ( DC ; ( SAB ) ) = d ( D ; ( SAB ) )Kẻ DH SADo AB AD và AB SA nên AB ( SAD )DH AB lại có DH SADH ( SAB )Nên d ( CD ; ( SAB ) ) = DH .Trong tam giác vuông SAD ta có :

Ví dụ 3: Cho hình chóp O.ABC có đường cao OH = 2a/3. Gọi M  và  N lần lượt là trung điểm của OA và OB. Khoảng cách giữa đường thẳng MN  và (ABC) bằng:

Hướng dẫn giải

Chọn DVì M và N lần lượt là trung điểm của OA và OB nênMN / / ABMN / / ( ABC )

Khi đó, ta có:

( vì M là trung điểm của OA ) .Xem thêm các dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác :

Giới thiệu kênh Youtube Tôi        Trang trước Trang sau

Video liên quan