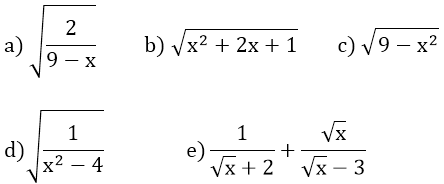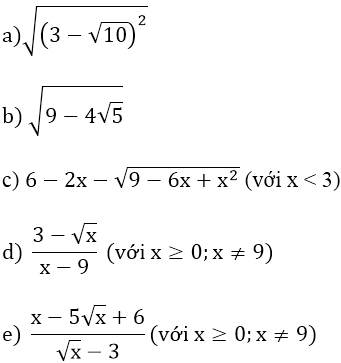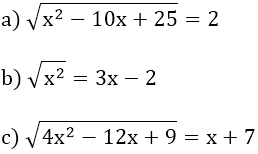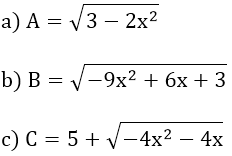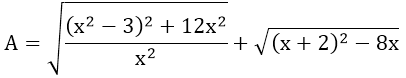bài tập căn bậc 2 lớp 9 có đáp án | Dương Lê

Bài tập tổng hợp về Căn bậc hai có giải thuật chi tiết cụ thể

Bài tập tổng hợp về Căn bậc hai có lời giải chi tiết

Bài 1: Tìm x để các căn thức bậc hai sau có nghĩa

Bài 2: Rút gọn các biểu thức sau:

Bài 3: Giải các phương trình sau:

Bài 4: Chứng minh rằng:

√ 2 + √ 6 + √ 12 + √ 20 + √ 30 + √ 42 Bài 5: Tìm giá trị lớn nhất của biểu thức:

Bài 6: Rút gọn biểu thức A

Bài 7: Cho biểu thức

a ) Rút gọn biểu thức M ;
b ) Tìm các giá trị của x để M = 4 .

Bài 8: Tìm giá trị nhỏ nhất của mỗi biểu thức:

Bài 9: Tìm x, để

Đáp án và hướng dẫn giải

Bài 1:

a ) x

Bài 2:

a ) √ 10 – 3 b ) √ 5 – 2

c) 6 – 2x – |x – 3|=

Bài 3:

a ) x = 3 hoặc x = 7
b ) x = 1

Bài 4:

√ 2 + √ 6 + √ 12 + √ 20 + √ 30 + √ 42 Bài 5:

a ) Giá trị lớn nhất của A là √ 3 khi x = 0

b) Giá trị lớn nhất của B là 2 khi x = 1/3

c ) Giá trị lớn nhất của C là 6 khi x = – 50%

Bài 6:

ĐKXĐ : x ≠ 0

Với x ≥ 2, A trở thành :

Với 0

Với x

Vậy

Bài 7:

Nếu x ≥ 3 thì M = 5 x – ( x – 3 ) = 4 x + 3
Nếu x Bài 8:

a ) Giá trị nhỏ nhất của A = 3/5 khi x = 1

Vậy Giá trị nhỏ nhất của B là 2, đạt được khi

⇔ 3 ≤ x ≤ 11

Bài 9:

Vì vế trái không âm nên vế phải

Do x2 + 1 > 0 ∀ x ∈ R nên 2 x + 1 ≥ 0 ⇔ x ≥ – 50%

⇔ 2 x + 1 = ( x2 + 1 ) ( 2 x + 1 )
⇔ ( 2 x + 1 ) [ 1 – ( x2 + 1 ) ] = 0

Vậy

Chuyên đề Toán 9 : không thiếu Lý thuyết và các dạng bài tập có đáp án khác :

• Lý thuyết Căn bậc hai
• Dạng 1: So sánh căn bậc hai số học
• Dạng 2: Tìm điều kiện để √A có nghĩa
• Dạng 3: Rút gọn biểu thức chứa căn bậc hai (dạng √(A2))
• Dạng 4: Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức chứa căn
• Bài tập tổng hợp về Căn bậc hai có lời giải chi tiết

Giới thiệu kênh Youtube VietJack

Ngân hàng trắc nghiệm lớp 9 tại duongleteach.com

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án