Đường Trung Tuyến Là Gì? Tính Chất đường Trung Tuyến Và Bài Tập | Lessonopoly

Đường trung tuyến là gì và có đặc thù gì chính là câu hỏi của nhiều bạn. Trong việc giải bài tập, dựng hình thì đường trung tuyến và đặc thù của đường trung tuyến được vận dụng rất nhiều. Bài viết sau đây, lessonopoly sẽ gửi đến bạn kiến thức và kỹ năng tương quan đến đường trung tuyến. Các bạn hãy cùng theo dõi nhé !

Định nghĩa đường trung tuyến

Đường trung tuyến của một đoạn thẳng là một đường thẳng đi qua trung điểm của đoạn thẳng đó .Trong hình học, trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối lập. Mỗi tam giác đều có ba trung tuyến. Đối với tam giác cân và tam giác đều, mỗi trung tuyến của tam giác chia đôi các góc ở đỉnh với hai cạnh kề có chiều dài bằng nhau .

Trong hình học không gian, khái niệm tương tự là mặt trung tuyến trong tứ diện.

Định nghĩa đường trung tuyến của tam giác

Đường trung tuyến của một tam giác là đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối lập trong hình học phẳng. Mỗi tam giác có 3 đường trung tuyến .Hãy tìm hiểu thêm video sau đây để hiểu thêm về đường trung tuyến nhé !

Tính chất đường trung tuyến trong tam giác

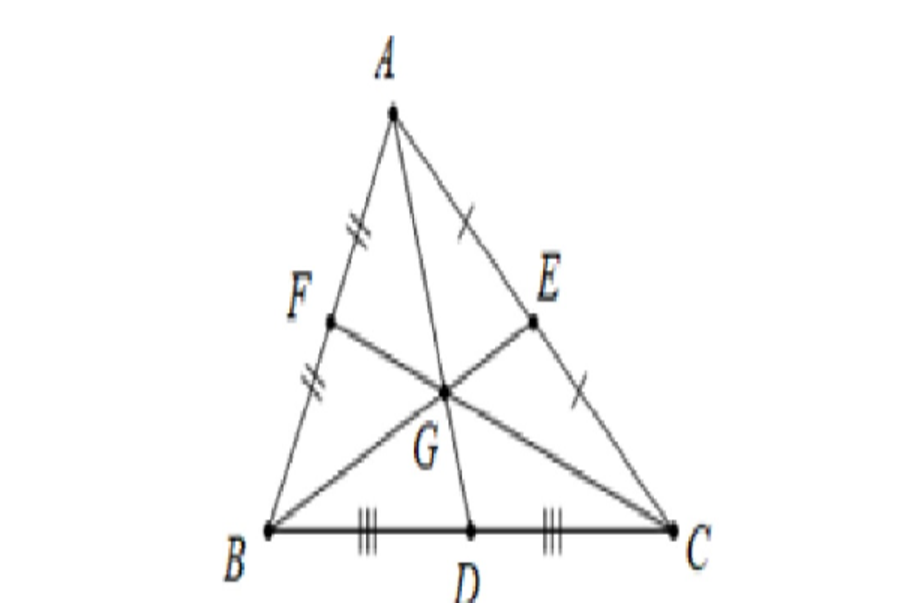
Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng chừng bằng 2 / 3 độ dài đường trung tuyến đi qua đỉnh ấy .Giao điểm của ba đường trung tuyến gọi là trọng tâm .Vị trí của trọng tâm tam giác : Trọng tâm của một tam giác cách mỗi đỉnh một khoảng chừng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy .Gọi G là trọng tâm của tam giác ABC, ABC có các trung tuyến AI, BM, CN thì ta sẽ có biểu thức :AG / AI = BG / BM = CG / CN = 2 / 3

Giao điểm của ba đường trung tuyến gọi là trọng tâm

Gọi G là trọng tâm của tam giác ABC, ABC có các trung tuyến AI, BM, CN thì ta sẽ có biểu thức :AG / AI = BG / BM = CG / CN = 2 / 3Xem thêm : Công thức tính diện tích quy hoạnh, tính chu vi tam giác thường và các tam giác đặc biệt quan trọng đúng mực nhấtXem thêm : Công thức tính chu vi, diện tích quy hoạnh hình chữ nhật cơ bản, kèm bài tập mẫu

Một số định lý đường trung tuyến trong tam giác

Thực hành : Cắt một tam giác bằng giấy. Gấp lại để xác lập trung điểm một cạnh của nó. Kẻ đoạn thẳng nối trung điểm này với đỉnh đối lập. Bằng cách tựa như, hãy vẽ tiếp hai đường trung tuyến còn lại .Quan sát tam giác vừa cắt ( trên đó đã vẽ ba đường trung tuyến ). Cho biết : Ba đường trung tuyến của tam giác này có cùng đi qua một điểm hay không ?Định lý 1 : Ba đường trung tuyến của một tam giác cùng đi qua một điểm. điểm gặp nhau của 3 đường trung tuyến gọi là trọng tâm ( centroid ) của tam giác đó .Định lý 2 : Đường trung tuyến của tam giác chia tam giác ấy thành hai tam giác có diện tích quy hoạnh bằng nhau. Ba trung tuyến chia tam giác thành 6 tam giác nhỏ với diện tích quy hoạnh bằng nhau .Ví dụ minh họa :Tam giác ΔABC có D, E, F là BC, CA, AB. Khi đó AD, BE, CF lần lượt là các đường trung tuyến xuất phát từ ba đỉnh A, B, C. AD, BE, CF đồng quy ở G .Ta có G là trọng tâm của tam giác ΔABC .Theo định nghĩa, AE = EC, CD = DB, BF = FA, do đó :SΔAGE = SΔCGE ; SΔBGD = SΔCGD ; SΔAGF = SΔBGF trong đó kí hiệu SΔABC là diện tích quy hoạnh của tam giác ABC .Điều này đúng bởi trong mỗi trường hợp hai tam giác có chiều dài đáy bằng nhau, và có cùng đường cao từ đáy, mà diện tích quy hoạnh của một tam giác thì bằng 50% chiều dài đáy nhân với đường cao, khi ấy hai tam giác ấy có diện tích quy hoạnh bằng nhau .Chúng ta có :SΔACG = SΔACD − SΔCGD ; SΔABG = SΔABD − SΔBGDDo đó ta có : SΔABG = SΔACG và SΔDBG = SΔDCG ; SΔCDG = 12S ΔACGDo SΔBGF = SΔAGF, SΔAGF = 12S ΔACG = SΔBGF = 12S ΔBCGDo vậy, SΔAFG = SΔBFG = SΔBGD = SΔCGDSử dụng cùng giải pháp này. ta hoàn toàn có thể chứng minh điều sau :SΔAFG = SΔBFG = SΔBGD = SΔCGD = SΔCGE = SΔAGEĐịnh lý 3 : Về vị trí trọng tâm : Trọng tâm của một tam giác cách mỗi đỉnh một khoảng chừng bằng 23 độ dài đường trung tuyến qua đỉnh ấy .Ví dụ như sau :Tam giác ΔABC có AD, BE, CF lần lượt là các đường trung tuyến xuất phát từ ba đỉnh A, B, C. Theo định lý 1 thì ba đường này đồng quy tại một điểm gọi là điểm G.Theo định lý 2 thì :AG = 2 / 3 ADBG = 2 / 3 BECG = 2 / 3 CF .

Định nghĩa đường trung tuyến trong tam giác đặc biệt

Tìm hiểu đường trung tuyến trong tam giác vuông

Tam giác vuông là một trường hợp đặc biệt quan trọng của tam giác, trong đó, tam giác sẽ có một góc có độ lớn là 90 độ, và hai cạnh tạo nên góc này vuông góc với nhau .Chính thế cho nên mà đường trung tuyến của tam giác vuông sẽ có khá đầy đủ những đặc thù của một đường trung tuyến tam giác .Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền .Một tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông .Ví dụ 1 :Tam giác ABC vuông ở B, độ dài đường trung tuyến BM sẽ bằng MA, MC và bằng 1 / 2 AC .trái lại nếu BM = 1 / 2 AC thì tam giác ABC sẽ vuông ở B .Ví dụ 2 :Tam giác ΔABC vuông ở A, độ dài đường trung tuyến AM sẽ bằng MB, MC và bằng 1 / 2 BC .trái lại nếu AM = 1 / 2 BC thì tam giác ΔABC sẽ vuông ở A .Chứng minh :Cho tam giác ΔABC. Gọi M là trung điểm của BC. Chứng minh rằng :Nếu = 90 độ thì MA = 1 / 2 BCNếu MA = 1 / 2 BC thì góc A bằng 90 độ .

Xét tam giác ΔABC có M là trung điểm của BC .

Trên tia đối của tia MA lấy điểm N sao cho MN = MA.

Ta có :

BM = CM ( giả thiết )MA = MN ( dựng hình )Suy ra : tam giác tam giác ΔMAB = tam giác tam giác ΔMNC ( c. g. c )

Bài tập ví dụ : Cho tam giác vuông ABC có hai cạnh góc vuông AB = 3 cm, AC = 4 cm. Tính khoảng cách từ đỉnh A tới trọng tâm G của tam giác ABC .Gợi ý giải : Sử dụng đặc thù đường trung tuyến của tam giác vuông : đường trung tuyến ứng với cạnh huyền thì có độ dài bằng 50% cạnh huyền và định lý Pitago .

Tìm hiểu đường trung tuyến trong tam giác cân, tam giác đều

Tính chất : Đường trung tuyến trong tam giác cân ( và tam giác đều ) ứng với cạnh đáy thì vuông góc với cái đấy và chia tam giác các thành hai tam giác bằng nhau .

Tam giác đều ΔABC có AM, BN, CP lần lượt là ba đường trung tuyến của tam giác. Theo đặc thù của đường trung tuyến trong tam giác đều ta có :AM ⊥ BC ; BN ⊥ AC ; CP ⊥ ABvà ΔABM = ΔACM ; ΔABN = ΔCBN ; ΔACP = ΔBCP .Bài tập ví dụ :Chứng minh trong một tam giác cân thì hai đường trung tuyến ứng với hai cạnh bên thì bằng nhauChứng minh định lý hòn đảo của định lý trên : Nếu tam giác có 2 đường trung tuyến bằng nhau thì tam giác đó cân .

Công thức liên quan tới độ dài của trung tuyến

Ta hoàn toàn có thể tính được độ dài đường trung tuyến của một tam giác trải qua độ dài các cạnh của tam giác ấy. Độ dài của trung tuyến được tính bằng định lý Apollonius như sau :Trong đó a, b và c là các cạnh của tam giác với các trung tuyến tương ứng ma, mb, mc từ trung điểm .Vậy là ta đã khám phá khá vừa đủ về định nghĩa và đặc thù của đường trung tuyến, cũng như vận dụng nó trong 1 số ít trường hợp đặc biệt quan trọng. Sau đây tất cả chúng ta hãy rèn luyện trải qua một số ít bài tập đơn thuần nhé .

Một số bài tập đường trung tuyến 

Bài 1: Cho hai đường thẳng x’x và y’y  gặp nhau ở O. Trên tia Ox lấy hai điểm A và B sao cho A nằm giữa O và B, AB=2OA. Trên y’y  lấy hai điểm L và M sao cho O là trung điểm của đoạn thẳng LM. Nối B với L, B với M và gọi P là trung điểm của đoạn thẳng MB, Q là trung điểm của đoạn thẳng LB.  Chứng minh các đoạn thẳng LP và MQ đi qua A.

Cách giải:

Ta có O là trung điểm của đoạn LM ( gt )Suy ra BO là đường trung tuyến của ΔBLM ( 1 )Mặt khác BO = BA + AO vì A nằm giữa O, B hay BO = 2 AO + AO = 3AO vì AB = 2AO ( gt )Suy ra AO = 1 / 3 BO, hay BA = 2 / 3 BO ( 2 )Từ ( 1 ) và ( 2 ) suy ra A là trọng tâm của ΔBLM ( đặc thù của trọng tâm )Mà LP và MQ là các đường trung tuyến của ΔBLM vì P. là trung điểm của đoạn thẳng MB ( gt )Suy ra các đoạn thẳng LP và MQ đều đi qua A ( đặc thù của ba đường trung tuyến )

Bài 2: Cho ΔABC có BM, CN là hai đường trung tuyến cắt nhau tại G. Kéo dài BM lấy đoạn ME=MG. Kéo dài CN lấy đoạn NF=NG. Chứng minh:

EF = BCĐường thẳng AG đi qua trung điểm BC .Cách giải :

a. ) Ta có BM và CN là hai đường trung tuyến gặp nhau tại G nên G là trọng tâm của tam giác ΔABC .⇒ GC = 2GNmà FG = 2GN ⇒ GC = GFTương tự BG, GE và góc G1 = góc G2 ( đd ). Do đó ΔBGC = ΔEGF ( c. g. c ) )Suy ra BC = EFb. ) G là trọng tâm nên AG chính là đường trung tuyến thứ ba trong tam giác ABCnên AG đi qua trung điểm của BC.

Trắc nghiệm tính chất ba đường trung tuyến của tam giác

Câu 1: Chọn câu sai:

Trong một tam giác có 3 đường trung tuyếnCác đường trung tuyến của tam giác cắt nhau tại một điểmGiao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đóMột tam giác có hai trọng tâm

Câu 2:  Điền số thích hợp vào chỗ chấm:”Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng… độ dài đường trung tuyến đi qua đỉnh ấy”

2 / 33 / 223

Câu 3: Cho tam giác ΔABC có đường trung tuyến AM = 9cm và trọng tâm G. Độ dài đoạn AG là:

4.5 cm

3 cm

6 cm4 cmBài viết trên đã gửi đến bạn những kỹ năng và kiến thức tương quan đến đường trung tuyến và đường trung tuyến của tam giác. Đường trung tuyến là kiến thức và kỹ năng được vận dụng rất nhiều trong các bài tập nên bạn hãy chú ý quan tâm và ghi nhớ những kiến thức và kỹ năng trên nhé ! Hy vọng bài viết trên hoàn toàn có thể giúp ích được cho bạn .