Lý thuyết Phép nhân và phép chia phân số Toán 6 KNTT với cuộc sống

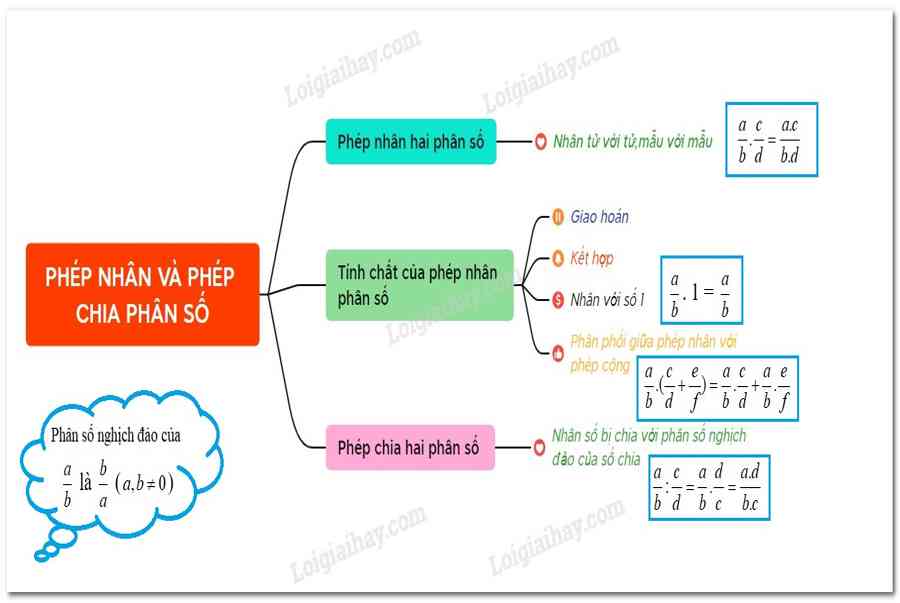
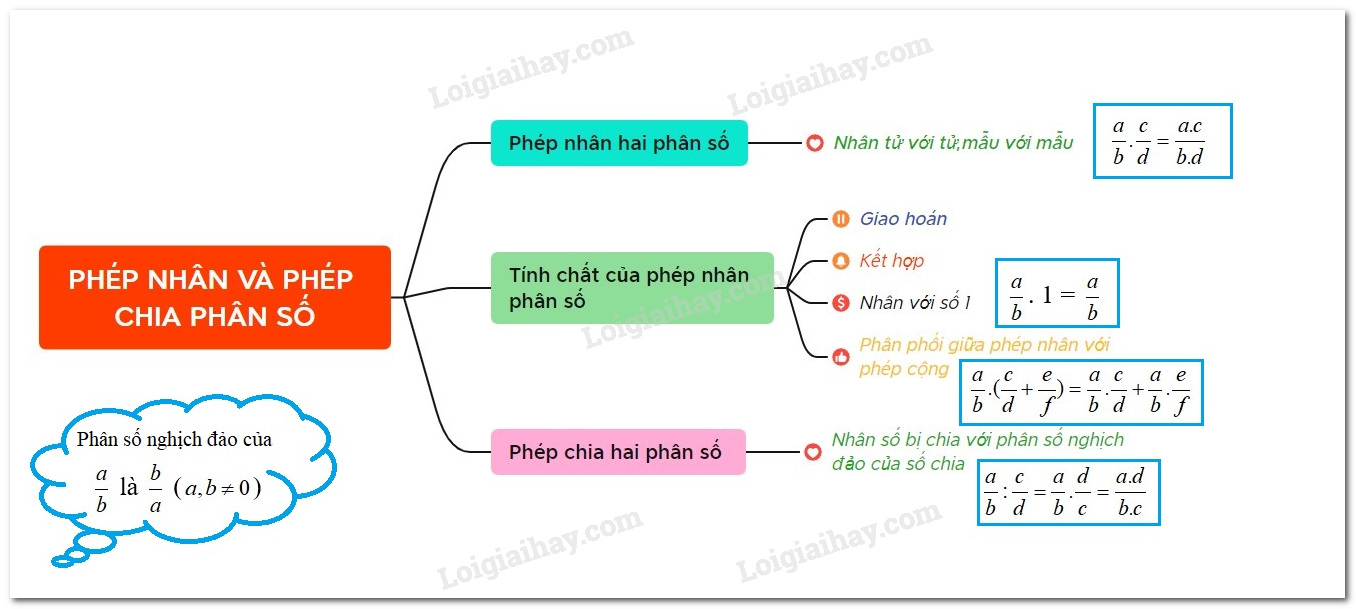
I. Nhân hai phân số

+ Muốn nhân hai phân số, ta nhân các tử số với nhau và nhân các mẫu với nhau .
USD \ dfrac { a } { b }. \ dfrac { c } { d } = \ dfrac { { a. c } } { { b. d } } $

+ Muốn nhân một số nguyên với một phân số (hoặc một phân số với một số nguyên), ta nhân số nguyên với tử của phân số và giữ nguyên mẫu: $a.\dfrac{b}{c} = \dfrac{{a.b}}{c}.$

Ví dụ:

a ) $ \ dfrac { { – 1 } } { 4 }. \ dfrac { 1 } { 5 } = \ dfrac { { \ left ( { – 1 } \ right ). 1 } } { { 4.5 } } = \ dfrac { { – 1 } } { { 20 } } $b ) USD 2. \ dfrac { 4 } { 5 } = \ dfrac { { 2.4 } } { 5 } = \ dfrac { 8 } { 5 } $ .

II. Một số tính chất của phép nhân phân số

+ Tính chất giao hoán : $ \ dfrac { a } { b }. \ dfrac { c } { d } = \ dfrac { c } { d }. \ dfrac { a } { b } $
+ Tính chất tích hợp : $ \ left ( { \ dfrac { a } { b }. \ dfrac { c } { d } } \ right ). \ dfrac { p } { q } = \ dfrac { a } { b }. \ left ( { \ dfrac { c } { d }. \ dfrac { p } { q } } \ right ) USD
+ Nhân với số USD 1 USD : $ \ dfrac { a } { b }. 1 = 1. \ dfrac { a } { b } = \ dfrac { a } { b } $, nhân với số USD 0 USD : $ \ dfrac { a } { b }. 0 = 0 USD
+ Tính chất phân phối của phép nhân so với phép cộng :
USD \ dfrac { a } { b }. \ left ( { \ dfrac { c } { d } + \ dfrac { p } { q } } \ right ) = \ dfrac { a } { b }. \ dfrac { c } { d } + \ dfrac { a } { b }. \ dfrac { p } { q } $

Ví dụ:

a) $\dfrac{{ – 3}}{{29}}.\dfrac{9}{{14}}.\dfrac{{ – 29}}{3} = \dfrac{{ – 3}}{{29}}.\dfrac{{ – 29}}{3}.\dfrac{9}{{14}} = \left( {\dfrac{{ – 3}}{{29}}.\dfrac{{ – 29}}{3}} \right).\dfrac{9}{{14}} = 1.\dfrac{9}{{14}} = \dfrac{9}{{14}}$

b )USD \ begin { array } { l } \ dfrac { 7 } { { 23 } }. \ dfrac { { 24 } } { { 11 } } + \ dfrac { 7 } { { 23 } }. \ dfrac { { – 2 } } { { 11 } } = \ dfrac { 7 } { { 23 } }. \ left ( { \ dfrac { { 24 } } { { 11 } } + \ dfrac { { – 2 } } { { 11 } } } \ right ) \ \ = \ dfrac { 7 } { { 23 } }. 2 = \ dfrac { { 14 } } { { 23 } } \ end { array }. $

III. Chia phân số

a) Số nghịch đảo

Hai số gọi là nghịch đảo của nhau nếu tích của chúng bằng USD 1 USD .

Ví dụ: Số nghịch đảo của $\dfrac{5}{6}$ là $\dfrac{6}{5}$; số nghịch đảo của $ – 5$ là $ – \dfrac{1}{5}$.

b) Qui tắc chia hai phân số

Muốn chia một phân số hay một số ít nguyên cho một phân số, ta nhân số bị chia với số nghịch đảo của số chia .
USD \ dfrac { a } { b } : \ dfrac { c } { d } = \ dfrac { a } { b }. \ dfrac { d } { c } = \ dfrac { { a. d } } { { b. c } } $
USD a : \ dfrac { c } { d } = a. \ dfrac { d } { c } = \ dfrac { { a. d } } { c } \ left ( { c \ ne 0 } \ right ) USD

Ví dụ: $\dfrac{{ – 1}}{6}:\dfrac{3}{{13}} = \dfrac{{ – 1}}{6}.\dfrac{{13}}{3} = \dfrac{{\left( { – 1} \right).13}}{{6.3}} = \dfrac{{ – 13}}{{18}}$.

CÁC DẠNG TOÁN VỀ PHÉP NHÂN, PHÉP CHIA PHÂN SỐ

I. Tìm số nghịch đảo của một số cho trước

+ Viết số cho trước dưới dạng $ \ dfrac { a } { b } \ left ( { a ; b \ in Z ; a ; b \ ne 0 } \ right ) USD+ Số nghịch đảo của $ \ dfrac { a } { b } $ là $ \ dfrac { b } { a } $+ Số USD 0 $ không có số nghịch đảo

+ Số nghịch đảo của số nguyên $ a { \ kern 1 pt } \ left ( { a \ ne 0 } \ right ) USD là $ \ dfrac { 1 } { a }. $

II. Thực hiện phép nhân, chia phân số

Áp dụng qui tắc chia hai phân số :Muốn chia một phân số hay một số ít nguyên cho một phân số, ta nhân số bị chia với số nghịch đảo của số chia .USD \ dfrac { a } { b } : \ dfrac { c } { d } = \ dfrac { a } { b }. \ dfrac { d } { c } = \ dfrac { { a. d } } { { b. c } } $ ; USD a : \ dfrac { c } { d } = a. \ dfrac { d } { c } = \ dfrac { { a. d } } { c } \ left ( { c \ ne 0 } \ right ) USD

III. Tìm số chưa biết trong một tích, một thương

+ Muốn tìm một trong hai thừa số, ta lấy tích chia cho thừa số đã biết
+ Muốn tìm số chia, ta lấy số bị chia chia cho thương
+ Muốn tìm số bị chia, ta lấy số chia nhân với thương.

IV. Tính giá trị biểu thức. So sánh giá trị hai biểu thức

– Ta sử dụng các qui tắc cộng, trừ, nhân, chia đã học và chú ý đến thứ tự thực hiện phép tính.
+ Đối với biểu thức không chứa ngoặc ta thực hiện theo thứ tự:

Lũy thừa$ \to $ nhân, chia $ \to $ cộng, trừ

+ Đối với biểu thức có dấu ngoặc ta thực thi theo thứ tự : $ \ left ( { } \ right ) \ to \ left [ { } \ right ] \ to \ left \ { { } \ right \ } $ .- Để so sánh giá trị hai biểu thức ta triển khai tính giá trị biểu thức rồi so sánh tác dụng .