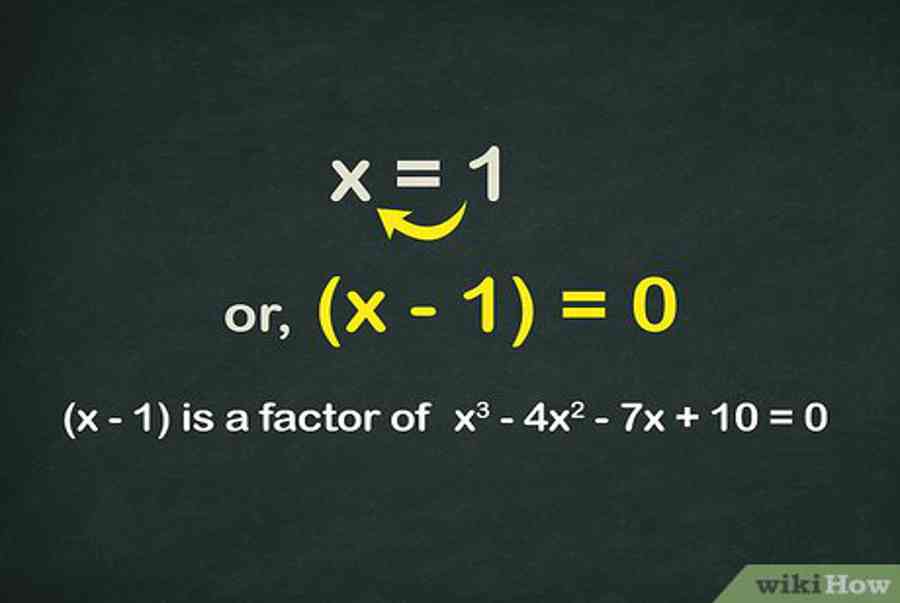Cách tách phương trình bậc 3 chứa tham số thành phương trình tích

tin tức tác giảNội dung chính

• Các bước
• Phần 1 của 2:Phân tích nhân tử bằng phương pháp nhóm
• Phần 2 của 2:Phân tích nhân tử sử dụng hạng tử tự do
• Lời khuyên
• Video liên quan

X

wikiHow là một trang “wiki”, nghĩa là nhiều bài viết ở đây là nội dung của nhiều tác giả cùng viết nên. Để tạo ra bài viết này, 24 người, trong đó có một số người ẩn danh, đã thực hiện chỉnh sửa và cải thiện bài viết theo thời gian.

Bài viết này đã được xem 83.620 lần.

Bài viết này sẽ hướng dẫn bạn cách nghiên cứu và phân tích đa thức bậc 3 thành nhân tử. Chúng ta sẽ cùng khám phá cách nghiên cứu và phân tích nhân tử bằng giải pháp đặt nhân tử chung và giải pháp sử dụng hạng tử tự do .

Các bước

Phần 1 của 2:Phân tích nhân tử bằng phương pháp nhóm

1Chia đa thức thành hai nhóm. Ta cần chia đa thức ra thành hai nhóm và xử lý mỗi nhóm một cách riêng biệt.

• Giả sử “xét đa thức.” x3 + 3×2 – 6x – 18 = 0. Ta nhóm đa thức thành hai phần (x3 + 3×2) và (- 6x – 18).

2Tìm nhân tử chung của trong mỗi nhóm.

• Ở nhóm (x3 + 3×2), ta có thể dễ dàng nhận ra x2 là nhân tử chung.
• Trong nhóm (- 6x – 18), -6 là nhân tử chung.

3Rút nhân tử chung ra ngoài mỗi nhóm.

• Rút x2 ra làm nhân tử chung của nhóm thứ nhất, ta được x2(x + 3).
• Rút -6 ra ngoài nhóm thứ hai, ta được -6(x+3).

4Nếu có một nhân tử xuất hiện trong cả hai nhóm, ta có thể gộp hai nhóm lại với nhau.

• Ta có (x + 3)(x2 – 6).

5Tìm nghiệm. Trong trường hợp ta có một nhân tử chứa x2, cần chú ý rằng cả hai giá trị âm và dương tính được từ nhân tử này đều thỏa mãn phương trình.

• Nghiệm của đa thức đang xét là -3, 6 và -6.

Phần 2 của 2:Phân tích nhân tử sử dụng hạng tử tự do

1Sắp xếp lại đa thức về dạng aX3+bX2+cX+d.

• Ví dụ, xét công thức x3 – 4×2 – 7x + 10 = 0.

2Tìm tất cả các nhân tử của “d”. Hằng số “d” là số không đi kèm với bất cứ biến số nào, trong trường hợp này biến số là “x”.

• Nhân tử của một số là những số mà ta có thể nhân chúng với một số khác để được một số khác. Trong trường hợp này, nhân tử của 10, hay “d,” là: 1, 2, 5, và 10.

3Tìm một nhân tử có thể khiến đa thức bằng 0. Ta muốn xác định nhân tử mà khi thế nhân tử này vào biến “x”, đa thức sẽ bằng 0.

• Thử với nhân tử đầu tiên, 1. Thế “1” vào tất cả các biến “x” trong đa thức:
  (1)3 – 4(1)2 – 7(1) + 10 = 0
• Ta được: 1 – 4 – 7 + 10 = 0.
• Vì 0 = 0 nên ta có x = 1 là một nghiệm của đẳng thức.

4Đảo vị trí. Nếu x = 1, ta có thể sắp xếp lại đẳng thức cho khác đi một chút mà không thay đổi ý nghĩa của nó.

• “x = 1” tương đương với “x – 1 = 0” hoặc “(x – 1)”. Tức là ta đã thực hiện phép trừ đi 1 ở cả hai vế của phương trình.

5Tách nghiệm ra khỏi phần còn lại của phương trình. “(x – 1)” chính là nghiệm. Hãy thử tách nghiệm này ra khỏi phương trình xem có được không. Tiến hành với từng đa thức một.

• Ta có thể tách (x  1) từ x3 không? Câu trả lời là không. Tuy nhiên, ta có thể mượn -x2 từ biến thứ hai và tiến hành tách nhân tử như sau: x2(x – 1) = x3 – x2.
• Ta có thể tách (x  1) ra khỏi phần còn lại của biến thứ hai không? Một lần nữa câu trả lời là không. Ta cần mượn tiếp một phần của biến thứ ba. Lấy 3x từ -7x và nhóm nhân tử chung với phần còn lại của biến thứ hai, ta được -3x(x – 1) = -3×2 + 3x.
• Vì ta đã mượn 3x từ -7x, do đó, biến thứ hai sẽ trở thành -10x, chú ý hạng tử tự do là 10. Ta có thể phân tích nhân tử không? Câu trả lời là có: -10(x – 1) = -10x + 10.
• Ta đã tách và sắp xếp lại các biến sao cho có thể nhóm được (x – 1) ra làm hạng tử chung cho cả biểu thức. Nhìn tổng quát, ta có biểu thức sau khi tách x3 – x2 – 3×2 + 3x – 10x + 10 = 0, biểu thức này cũng tương đương với x3 – 4×2 – 7x + 10 = 0.

6Tiếp tục thế nghiệm của hạng tử tự do. Xét những số đã tách ra khi rút (x  1) ra làm nhân tử chung ở bước 5:

• x2(x – 1) – 3x(x – 1) – 10(x – 1) = 0. Ta có thể sắp xếp lại đẳng thức này để dễ phân tích nhân tử hơn: (x – 1)(x2 – 3x – 10) = 0.
• Đến đây, ta cần phân tích nhân tử đối với (x2 – 3x – 10). Biểu thức này phân tích được thành (x + 2)(x – 5).

7Đáp án của phương trình chính là nghiệm đã được tách ra. Ta có thể kiểm tra xem kết quả thu được có chính xác là nghiệm của phương trình hay không bằng cách thế giá trị tìm được vào các biến của đa thức ban đầu.

• (x – 1)(x + 2)(x – 5) = 0, tức là 1, -2 và 5 là nghiệm của đa thức.
• Thế -2 vào phương trình ban đầu ta được: (-2)3 – 4(-2)2 – 7(-2) + 10 = -8 – 16 + 14 + 10 = 0.
• Thế 5 vào phương trình ban đầu, ta được (5)3 – 4(5)2 – 7(5) + 10 = 125 – 100 – 35 + 10 = 0.

Lời khuyên

• Đối với số thực, không có đa thức bậc 3 nào là không thể phân tích thành nhân tử vì tất cả bậc ba đều có ít nhất một nghiệm thực. Với những đa thức không có nghiệm thực phù hợp, ví dụ x^3 + x + 1, ta không thể phân tích thành các đa thức nếu sử dụng số thực cùng với các hệ số hợp lý. Dù có thể tính nghiệm của đa thức này theo công thức nghiệm phương trình bậc ba, nhưng bản thân nó lại không thể tách được thành các đa thức nguyên.
• Đa thức bậc ba là tích của ba đa thức bậc nhất hoặc là tích của một đa thức bậc nhất với một đa thức bậc hai không thể tách thành nhân tử. Trong trường hợp này, sau khi đã tìm được nhân tử chung bậc nhất, ta có thể thực hiện phép chia đa thức cho đa thức để tìm ra đa thức bậc hai.

Video liên quan