Cách giải phương trình bậc 2 và tính nhẩm nghiệm PT bậc 2

Bài viết này Trung tâm Gia sư Hà Nội chia sẻ với các em cách giải phương trình bậc 2 và tính nhẩm nghiệm của PT bậc 2 trong trường hợp đặc biệt.

Có nhiều dạng toán trong chương trình Toán 9 và ôn thi vào lớp 10 môn Toán cần phải biết giải pháp giải phương trình bậc 2 thì mới làm được .

Định nghĩa phương trình bậc 2

Phương trình bậc hai là phương trình có dạng : ax2 + bx + c = 0. Với

• x là ẩn số
• a, b, c là các số đã biết sao cho: a ≠ 0
• a, b, c là những hệ số của phương trình và có thể phân biệt bằng cách gọi tương ứng với hệ số của x (theo phương trình trên thì a là hệ số bậc hai, b là hệ số bậc một, c là hằng số hay số hạng tự do).

Phương pháp giải phương trình bậc 2

Giải phương trình bậc 2 : ax2 + bx + c = 0 theo biệt thức delta ( Δ )

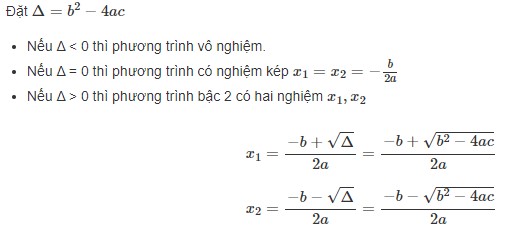
Định lý Vi-ét với PT bậc 2

Công thức Vi-ét về quan hệ giữa các nghiệm của đa thức với các thông số của nó. Trong trường hợp phương trình bậc hai một ẩn, được phát biểu như sau :

Một số trường hợp đặc biệt quan trọng của PT bậc 2

Nếu phương trình bậc 2 có :

Cách tính nhẩm nghiệm phương trình bậc 2

Xuất phát từ định lý Vi-ét, tất cả chúng ta có các dạng toán tính nhẩm như sau :

Dạng 1 : A = 1, B = Tổng, C = Tích

Nếu phương trình có dạng x2 – ( u + v ) x + uv = 0 thì phương trình đó có hai nhiệm u và v .Nếu phương trình có dạng x2 + ( u + v ) x + uv = 0 thì phương trình có hai nghiệm – u và – v .

Tóm lại:

• x2 – (u+v)x + uv = 0 => x1 = u, x2 = v (1)
• x2 + (u+v)x + uv = 0 => x1 = -u, x2 = -v

Như vậy, với dạng này tất cả chúng ta cần thực thi 2 phép nhẩm : “ Phân tích thông số c thành tích và b thành tổng ”. Trong hai phép nhẩm đó, tất cả chúng ta nên nhẩm thông số c trước rồi tích hợp với b để tìm ra hai số thỏa mãn nhu cầu tích bằng c và tổng bằng b .

Khi tiến hành, bạn nhẩm trong đầu như sau: Tích của hai nghiệm bằng c, mà tổng lại bằng b.

Ví dụ phương trình :

x2 – 5x + 6 = 0
Nhẩm: “Tích của hai nghiệm bằng 6, mà tổng lại bằng 5”. Hai số đó là: 2 và 3 vì 6 = 2×3 và 5 = 2 + 3. Vậy phương trình có hai nghiệm x = 2, x = 3.

x2 – 7x + 10 = 0
Nhẩm: “Tích của hai nghiệm bằng 10, mà tổng lại bằng 7”. Hai số đó là: 2 và 5 vì 10 = 2×5 và 7 = 2 + 5. Vậy phương trình có hai nghiệm x = 2, x = 5.

Dạng 2 : A + B + C = 0 và A – B + C = 0

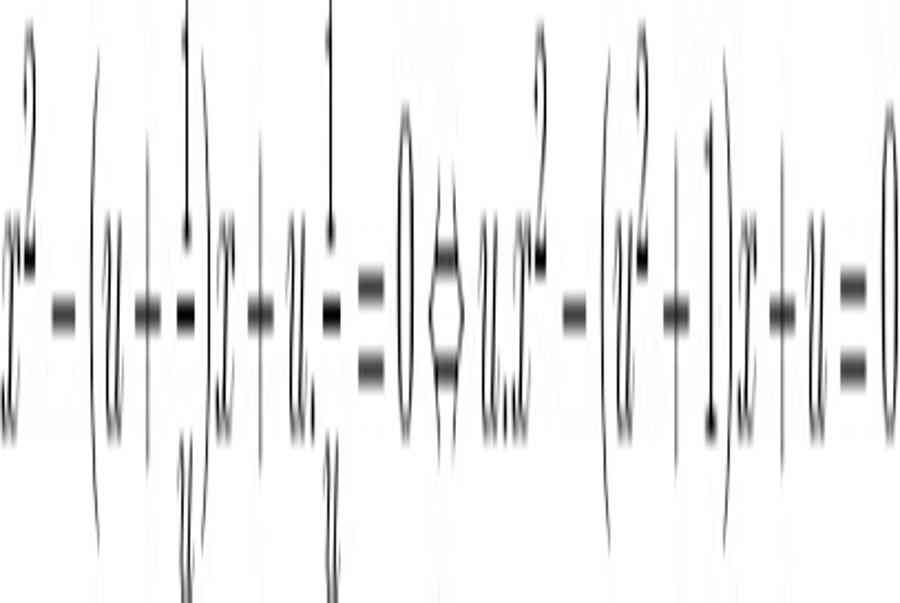
x2 – ( u + v ) x + uv = 0 => x1 = u, x2 = v ( 1 )

• Nếu thay v = 1 vào (1) thì chúng ta sẽ có trường hợp nhẩm nghiệm quen thuộc a + b + c = 0, với a = 1, b = -(u+1), c = u.
• Nếu thay v = -1 vào (1) thì bạn sẽ có trường hợp nhẩm nghiệm a – b + c = 0, với a = 1, b = -(u-1), c = -u.

Do loại này đã quá quen thuộc và thường gặp, nên bài viết không xét các ví dụ cho trường hợp này mà tập trung chuyên sâu vào Dạng 1 và Dạng 3 .

Dạng 3 : Hai nghiệm là nghịch đảo của nhau

Nếu u ≠ 0 và v = 1 / u thì phương trình ( 1 ) có dạng :

Khi đó : Phương trình có hai nghiệm là nghịch đảo của nhau x = u, x = 1 / u. Đây cũng là trường hợp hay gặp khi giải toán. Ví dụ phương trình :

• 2×2 – 5x + 2 = 0 có hai nghiệm x = 2, x = 1/2
• 3×2 – 10x + 3 = 0 có hai nghiệm x = 3, x = 1/3

Các ví dụ giải PT bậc 2

Bài tập tự giải các PT bậc 2

1. 2×2 + 6x + 5 = 0
2. x2 – 4x + 4 = 0
3. 2×2 + 7x – 3 = 0.

Bồi dưỡng Toán 9 – Tags: bậc 2, phương trình, phương trình bậc 2, tính nhẩm, tính nhẩm nghiệm