Cách tính đường cao trong tam giác đều

Cách tính đường cao trong tam giác đềuCông thức tính đường cao trong tam giác đều là một trong những công thức toán cơ bản bạn nên biết. Nếu còn chưa biết công thức này hoặc đơn thuần là đã quá lâu bạn không sử dụng nên quên mất. Vậy thì hãy cùng webloikhuyen khám phá lại cách tính đường cao trong tam giác đều nhé .

Tam giác đều là gì?

Tam giác đều là tam giác có 3 cạnh bằng nhau hoặc tương tự với 3 góc bằng nhau và bằng 60 độ. Nó là một đa giác đều với số cạnh bằng 3

Dấu hiệu nhận biết tam giác đều

+ Tam giác có 3 cạnh bằng nhau+ Tam giác có 3 góc bằng nhau+ Tam giác cân có 1 góc bằng 60 độ là tam giác đều+ Tam giác có 2 góc bằng 60 độ .

Đường cao trong tam giác đều

Đường cao trong tam giác

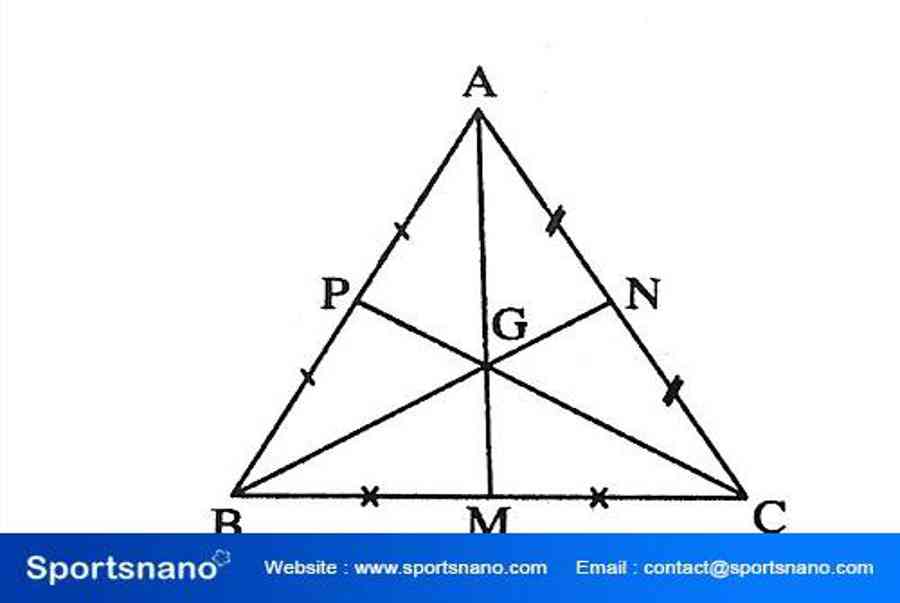
Đoạn vuông góc kẻ từ 1 đỉnh đến đường thẳng chứa cạnh đối lập gọi là đường cao của tam giác đó. Mỗi tam giác có 3 đường caoBa đường cao của tam giác đi qua một điểm, điểm đó gọi là trực tâm của tam giácTính chất 3 đường cao trong tam giác đều : Trong 1 tam giác đều, trọng tâm, trực tâm, điểm cách đều 3 đỉnh, điểm nằm trong tam giác và cách đều ba cạnh là 4 điểm trùng nhau .

Công thức tính đường cao
trong tam giác

Có nhiều công thức tính đường cao trong tam giác. Cách tính đơn thuần nhất được nhiều người biết đến là công thức HeronTa có+ a, b, c là độ dài 3 cạnh của tam giác

+ h(a) là độ dài đường cao kẻ từ đỉnh A xuống cạnh BC

+ p là nửa chua vi tam giác với p = ( a + b + c ) / 2Từ đó có công thức tính đường cao trong tam giác là[ h ( a ) ] ^ 2 = p ( 4 / a ^ 2 ) ( p-a ) ( p-b ) ( b-c )Ví dụ : Tính chiều dài đường cao trong tam giác có độ dài 3 cạnh lần lượt là 2,3,4 ( cm )Ta có nửa chu vi của tam giác p = ( a + b + c ) / 2 = 4.5Áp dụng công thức trên ta có :Độ dài đường cao trong tam giác [ h ( a ) ] ^ 2 = 8.4375 => h ( a ) = 2.9 ( cm )

Công thức tính đường cao trong tam giác đều

Ta có a là độ dài 3 cạnh của tam giác đều, h là độ dài đường cao trong tam giác đều .Từ đó ta có công thức tính đường cao trong tam giác đều làh = a * [ ( căn 3 ) / 2 )

Ví dụ : Tính chiều dài đường cao trong tam giác đều có độ dài 3 cạnh
là 2 (cm)

Áp dụng công thức trên ta có :Độ dài đường cao trong tam giác đều h = 2 * [ ( căn 3 ) / 2 ) = 1.73 ( cm )Công thức tính đường cao trong tam giác đều thật đơn thuần phải không nào ? Tùy từng trường hợp mà vận dụng cho đúng chuẩn nhé. Chúc bạn thành công xuất sắc .