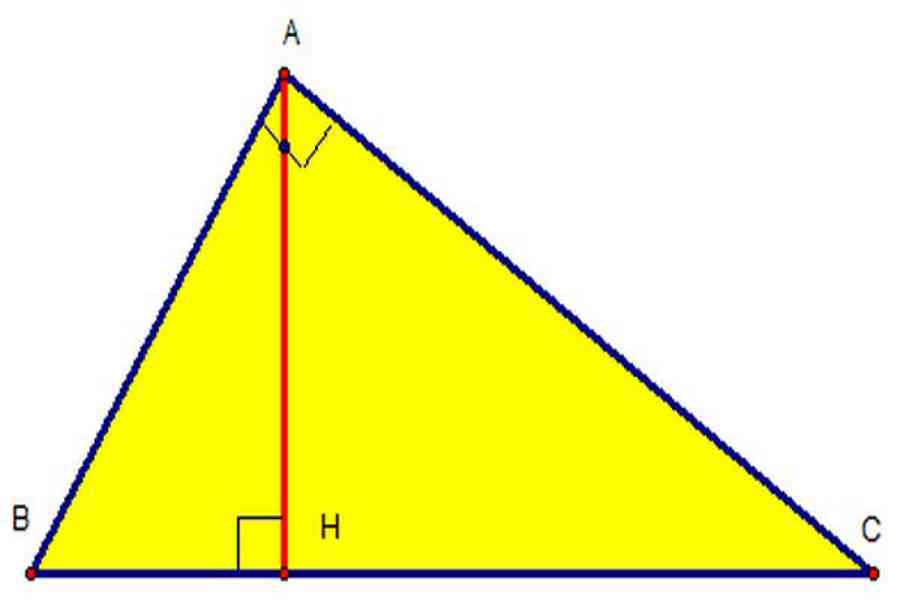
Tam giác vuông
Khái niệm

– AC, AB là hai cạnh góc vuông.
– AH là chiều cao của tam giác ABC– Bảo hành là hình chiếu của AB lên cạnh huyền BC .– CH là hình chiếu của AC lên cạnh huyền BC .
Định lý Pitago
-
Định lý Pytago
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng những bình phương của hai cạnh góc vuông .Tam giác ABC vuông tại A thì ta có :BC2 = AB2 + AC2 .
-
Định lý Pytago đảo
Nếu một tam giác có bình phương của một cạnh bằng tổng những bình phương của hai cạnh kia thì tam giác đó là tam giác vuông .Tam giác ABC có BC2 = AB2 + AC2=> Góc BAC = 90 o .
-
Hệ thức về cạnh và đường cao trong tam giác vuông. a)
AB2= BC.BH ; AC2= BC.CH b )AH2= BH.CH c )AB.AC = BC.AH
d)
-
Tỉ số lượng giác của góc nhọn trong tam giác vuông
-
Tỉ số lượng giác của 2 góc phụ nhau thì:
sinα = cosβ, cosα = sinβ, tanα = cotβ, cotα = tanβ
- Một số tính chất của tỉ số lượng giác
-
Hệ thức về cạnh và góc trong tam giác vuông
– Cạnh góc vuông = cạnh huyền. sin góc đốiAC = BC.sinB, AB = BC.sin C– Cạnh góc vuông = cạnh huyền. cos góc kềAC = BC.cosC, AB = BC.cosB– Cạnh góc vuông 1 = cạnh góc vuông 2.tan góc đối– Cạnh góc vuông 1 = cạnh góc vuông 2.cot góc kề
Trả lời câu hỏi Tam giác vuông tại A
Ví dụ 1:
Cho tam giác ABC vuông tại A. Tính tổng góc B + góc C
Giải:
Vì tam giác ABC vuông tại A => góc A = 90 oTa lại có : Tổng 3 góc trong một tam giác bằng 180 o=> góc B + góc C + góc A = 180 o=> góc B + góc C = 180 o – 90 o = 90 o .Vậy tổng góc B + góc C bằng 90 o .
Ví dụ 2:
Tính những số đo x, y ở những hình 47, 48, 49, 50, 51 .
Giải:
Áp dụng định lý tổng ba góc trong một tam giác bằng 180 º ta có :
– Hình 47
x + 90 o + 55 o = 180 ox = 180 o – 90 o – 55 ox = 35 o
– Hình 48
x + 30 o + 40 o = 180 ox = 180 o – 30 o – 40 ox = 110 o
– Hình 49
x + x + 50 o = 180 o2 x = 180 o – 50 ox = 65 o
– Hình 50
Áp dụng định lý góc ngoài của tam giác ta có :y = 60 o + 40 oy = 100 ox + 40 o = 180 o ( 2 góc kề bù )x = 140 o
– Hình 51
Áp dụng định lý góc ngoài trong tam giác ABD có: x = 70o + 40o = 110o
Áp dụng định lý tổng ba góc trong tam giác ADC có :y + 110 o + 40 o = 180 o=> y = 30 o .
Bài tập tam giác vuông: Cho tam giác ABC vuông tại A…
Bài 1
Cho tam giác vuông ABC có AB = 5 cm ; AC = 12CM, BC = 13 CMa ) Chứng minh tam giác ABC vuông tại A và tính độ dài đường cao AHb ) Kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F. Chứng minh AE.AB = AF.AC.
Giải:
a ) Ta có AB2 = 52 = 25, AC2 = 122 = 144, BC2 = 132 = 169Ta thấy BC2 = AB2 + AC2=> Tam giác ABC vuông tại A ( định lý Pitago hòn đảo ) .b ) Theo hệ thức cạnh và đường cao trong tam giác vuôngXét tam giác AHB vuông tại H. Ta có :HA2 = AB.AE ( 1 )Xét tam giác AHC vuông tại H. Ta có :HA2 = AF.AC ( 2 )Từ ( 1 ) và ( 2 ) => AE.AB = AF.AC ( điều phải chứng tỏ ) .
Bài 2
Cho tam giác ABC vuông tại A, đường cao AH, biết HB = 3,6 cm, HC = 6,4 cma ) Tính độ dài cạnh AB, AC, AH .b ) Kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F. Chứng minh AE.AB = AF.AC
Bài 3
Cho hình chữ nhật ABCD. Từ D hạ đường vuông góc xuống AC cắt AC tại H. Biết rằng AB = 13 cm, DH = 5 cm, tính độ dài BD .
Bài 4
Cho tam giác ABC vuông tại A, có AB = 3 cm, AC = 4 cm và AHa ) tính BC, AHb ) Tính góc B, góc Cc ) Phân giác của góc A cắt BC tại E. Tính BE, CE .
Bài 5
Cho tam giác ABC vuông tại A, đường cao AH = 6 cm, HC = 8 cma ) Tính độ dài HB, AB, ACb ) Kẻ HD vuông giác với AC ( D ∈ AC ). Tính độ dài HD và diện tích quy hoạnh tam giác AHD .
Bài 6
Cho tam giác ABC vuông tại A, AB = 3 cm, AC = 4 cm .a ) Tính BCb ) Phân giác của góc A cắt BC tại E. Tính BE, CE .c ) Từ E kẻ EM và EN vuông góc với AB, AC. Hỏi tứ giác AMEN là hình gì ? Tính diện tích quy hoạnh AMEN .
Bài 7
Cho tam giác ABC vuông tại A đường cao AH, BH = 9 cm, CH = 25 cm. Tính AH, AB ?
Bài 8
Cho tam giác ABC, BC = 15 cm, góc B = 34 o, góc C = 40 o, kẻ AH vuông góc BC ( H ∈ BC ). Tính AH ?
Bài 9
Cho tam giác ABC vuông tại A, có AB = 6 cm, AC = 8 cm .a ) Tính BC, góc B, góc Cb ) Đường phân giác góc A cắt BC tại D. Tính BD, CD .
Bài 10
Cho tam giác vuông tại A, góc C = 30 o, BC = 10 cma ) Tính AB, ACb ) Kẻ AM, AN lần lượt vuông góc với đường phân giác trong và ngoài của B. Chứng minh AN / / BC, AB / / MN.c ) Chứng minh tam giác MAB đồng dạng với tam giác ABC
Bài 11
Cho tam giác ABC vuông tại A, AB
Bài 12
Cho tam giác ABC nội tiếp đường tròn ( O ). Một đường tròn tâm I tùy ý đi qua B và C, cắt AB và AC theo thứ tự ở M và N. Đường tròn tâm K ngoại tiếp tam giác AMN cắt đường tròn ( O ) tại điểm thứ hai D. Chứng minh rằng :a ) AKIO là hình bình hành .b ) góc ADI = 90 o .
Bài 13
Cho nửa đường tròn tâm O đường kính AB, điểm C thuộc nửa đường kính OA. Đường vuông góc với AB tại C cắt nửa đường tròn ở D. Đường tròn tâm I tiếp xúc với nửa đường tròn và tiếp xúc với những đoạn thẳng CA, CD. Gọi E là tiếp điểm trên AC của đường tròn ( I ) .a ) Chứng minh rằng BD = BE .b ) Suy ra cách dựng đường tròn ( I ) nói trên .
Bài 14
Cho tam giác ABC nội tiếp đường tròn ( O ). Tia phân giác của góc A cắt BC ở D, cắt đường tròn ở E. Gọi M, N theo thứ tự là hình chiếu của D trên AB, AC. Gọi I, K theo thứ tự là hình chiếu của E trên AB, AC. Chứng minh rằng :a ) AI + AK = AB + AC ;b ) Diện tích tứ giác AMEN bằng diện tích quy hoạnh tam giác ABC .
Bài 15
Qua điểm A ở bên ngoài đường tròn ( O ), kẻ cát tuyến ABC với đường tròn. Các tiếp tuyến của đường tròn tại B và C cắt nhau ở K. Qua K kẻ đường thẳng vuông góc với AO, cắt AO tại H và cắt đường tròn ( O ) tại E và F ( E nằm giữa K và F ). Gọi M là giao điểm của OK và BC. Chứng minh rằng :a ) EMOF là tứ giác nội tiếp .b ) AE, AF là những tiếp tuyến của đường tròn ( O ) .
Bài 16
Cho tam giác ABC cân tại A, AB = 16, BC = 24, đường cao AE. Đường tròn tâm O nội tiếp tam giác ABC tiếp xúc AC tại F .a ) Chứng minh rằng OECF là tứ giác nội tiếp và BF là tiếp tuyến của đường tròn ngoại tiếp tứ giác đó .b ) Gọi M là giao điểm của BF với đường tròn ( O ). Chứng minh rằng BMOC là tứ giác nội tiếp .
Bài 17
Cho tam giác ABC vuông tại A, đường cao AH. Gọi ( P. ), ( Q. ) theo thứ tự là đường tròn nội tiếp hai tam giác AHB và AHC. Kẻ tiếp tuyến chung ngoài ( khác BC ) của hai đường tròn ( P. ) và ( Q. ), nó cắt AB, AH, AC theo thứ tự ở M, K, N. Chứng minh rằng :a ) Các tam giác HPQ và ABC đồng dạng .b ) KP / / AB, KQ / / AC .
c) BMNC là tứ giác nội tiếp.
d ) Năm điểm A, M, P., Q., N thuộc cùng một đường tròn .e ) Tam giác AED vuông cân ( D, E theo thứ tự là giao điểm của PQ với AB, AC ) .Trên đây là kim chỉ nan và bài tập về dạng toán cho tam giác ABC vuông tại A. Các em hãy tập giải dạng toán này vì đây là dạng toán trọng tâm của phần toán Hình. Nếu cần tương hỗ giải đáp hãy để lại comment cho lessonopoly nhé những em. Chúc những em học tốt .
Source: http://139.180.218.5
Category: tản mạn