Công thức toán lớp 5

4.7 / 5 – ( 3 bầu chọn )

A. Phép cộng

I. Công thức tổng quát:

II. Tính chất:

1. Tính chất giao hoán:

Kết luận : Khi đổi chỗ những số hạng trong một tổng thì tổng không đổi khác .
Công thức tổng quát : a + b = b + a

2. Tính chất kết hợp:

Kết luận : Khi cộng tổng hai số với số thứ ba, ta hoàn toàn có thể cộng số thứ nhất với tổng hai số còn lại .
Công thức tổng quát : ( a + b ) + c = a + ( b + c )

3. Tính chất: Cộng với 0:

Kết luận : Bất kì 1 số ít cộng với 0 cũng bằng chính nó .
CTTQ : a + 0 = 0 + a = a

B. Phép trừ

I. Công thức tổng quát:

II. Tính chất:

1. Trừ đi 0:

Kết luận : Bất kì một số ít trừ đi 0 vẫn bằng chính nó .
CTTQ : a – 0 = a

2. Trừ đi chính nó:

Kết luận : Một số trừ đi chính nó thì bằng 0 .
CTTQ : a – a = 0

3. Trừ đi một tổng:

Kết luận : Khi trừ một số ít cho một tổng, ta hoàn toàn có thể lấy số đó trừ dần từng số hạng của tổng đó .
CTTQ : a – ( b + c ) = a – b – c = a – c – b

4. Trừ đi một hiệu:

Kết luận : Khi trừ 1 số ít cho một hiệu, ta hoàn toàn có thể lấy số đó trừ đi số bị trừ rồi cộng với số trừ .
CTTQ : a – ( b – c ) = a – b + c = a + c – b

C. Phép nhân

I. Công thức tổng quát

II. Tính chất:

1. Tính chất giao hoán:

Kết luận : Khi đổi chỗ những thừa số trong một tích thì tích không biến hóa .
CTTQ : a × b = b × a

2. Tính chất kết hợp:

Kết luận : Muốn nhân tích hai số với số thứ ba, ta hoàn toàn có thể nhân số thứ nhất với tích hai số còn lại .
CTTQ : ( a × b ) × c = a × ( b × c )

3. Tính chất: nhân với 0:

Kết luận : Bất kì một số ít nhân với 0 cũng bằng 0 .
CTTQ : a × 0 = 0 × a = 0

4. Tính chất nhân với 1:

Kết luận : Một số nhân với 1 thì bằng chính nó .
CTTQ : a × 1 = 1 × a = a

5. Nhân với một tổng:

Kết luận : Khi nhân 1 số ít với một tổng, ta hoàn toàn có thể lấy số đó nhân với từng số hạng của tổng rồi cộng những tác dụng với nhau .
CTTQ : a × ( b + c ) = a × b + a × c

6. Nhân với một hiệu:

Kết luận : Khi nhân một số ít với một hiệu, ta hoàn toàn có thể lấy số đó nhân với số bị trừ và số trừ rồi trừ hai hiệu quả cho nhau .
CTTQ : a × ( b – c ) = a × b – a × c

D. Phép chia

I. Công thức tổng quát:

Phép chia còn dư:

a : b = c (dư r)

số bị chia số chia thương số dư
Chú ý : Số dư phải bé hơn số chia .

II. Công thức:

1. Chia cho 1: Bất kì một số chia cho 1 vẫn bằng chính nó.

CTTQ : a : 1 = a

2. Chia cho chính nó: Một số chia cho chính nó thì bằng 1.

CTTQ : a : a = 1

3. 0 chia cho một số: 0 chia cho một số bất kì khác 0 thì bằng 0

CTTQ : 0 : a = 0

4. Một tổng chia cho một số: Khi chia một tổng cho một số, nếu cácsố hạng của tổng đều chia hết cho số đó, thì ta có thể chia từng số hạng cho số chia rồi cộng các kết quả tìm được với nhau.

CTTQ : ( b + c ) : a = b : a + c : a

5. Một hiệu chia cho một số: Khi chia một hiệu cho một số, nếu số bị trừ và số trừ đều chia hết cho số đó, thì ta có thể lấy số bị trừ và số trừ chia cho số đó rồi trừ hai kết quả cho nhau.

CTTQ : ( b – c ) : a = b : a – c : a

6. Chia một số cho một tích: Khi chia một số cho một tích, ta có thể chia số đó cho một thừa số, rồi lấy kết quả tìm được chia tiếp cho thừa số kia.

CTTQ : a : ( b × c ) = a : b : c = a : c : b

7. Chia một tích cho một số: Khi chia một tích cho một số, ta có thể lấy một thừa số chia cho số đó (nếu chia hết), rồi nhân kết quả với thừa số kia.

CTTQ : ( a × b ) : c = a : c × b = b : c × a

E. Tính chất chia hết

1, Chia hết cho 2 : Các số có tận cùng là 0, 2, 4, 6, 8 ( là những số chẵn ) thì chia hết cho 2 .
VD : 312 ; 54768 ; … .
2, Chia hết cho 3 : Các số có tổng những chữ số chia hết cho 3 thì chia hết cho 3 .
VD : Cho số 4572
Ta có 4 + 5 + 7 + 2 = 18 ; 18 : 3 = 6 Nên 4572 : 3 = 1524
3, Chia hết cho 4 : Các số có hai chữ số tận cùng chia hết cho 4 thì chia hết cho 4 .
VD : Cho số : 4572
Ta có 72 : 4 = 18 Nên 4572 : 4 = 11 4 3
4, chia hết cho 5 : Các số có tận cùng là 0 hoặc 5 thì chia hết cho 5 .
VD : 5470 ; 7635
5, Chia hết cho 6 ( Nghĩa là chia hết cho 2 và 3 ) : Các số chẵn và có tổng những chữ số chia hết cho 3 thì chia hết cho 6 .
VD : Cho số 1356
Ta có 1 + 3 + 5 + 6 = 15 ; 15 : 3 = 5 Nên 1356 : 3 = 452
6, Chia hết cho 10 ( Nghĩa là chia hết cho 2 và 5 ) : Các số tròn chục ( có hàng đơn vị chức năng bằng 0 ) thì chia hết cho 10 .
VD : 130 ; 2790
7, Chia hết cho 11 : Xét tổng những chữ số ở hàng chẵn bằng tổng những chữ số ở hàng lẻ thì số đó chia hết cho 11 .
VD : Cho số 48279
Ta có 4 + 2 + 9 = 8 + 7 = 15 Nên 48279 : 11 = 4389
8, Chia hết cho 15 ( Nghĩa là chia hết cho 3 và 5 ) : Các số có chữ số hàng đơn vị chức năng là 0 ( hoặc 5 ) và tổng những chữ số chia hết cho 3 thì chia hết cho 15 .
VD : Cho số 5820
Ta có 5 + 8 + 2 + 0 = 15 ; 15 : 3 = 5 Nên 5820 : 15 = 388
9, Chia hết cho 36 ( Nghĩa là chia hết cho 4 và 9 ) : Các số có hai chữ số tận cùng chia hết cho 4 và tổng những chữ số chia hết cho 9 thì chia hết cho 36 .
VD : Cho số : 45720
Ta có 20 : 4 = 5 và ( 4 + 5 + 7 + 2 + 0 ) = 18
18 : 9 = 2 Nên 45720 : 36 = 1270

F. Toán Trung bình cộng

1. Muốn tìm trung bình cộng ( TBC ) của nhiều số, ta tính tổng của những số đó rồi chia tổng đó cho số những số hạng .
CTTQ : TBC = tổng những số : số những số hạng
2. Tìm tổng những số : ta lấy TBC nhân số những số hạng
CTTQ : Tổng những số = TBC × số những số hạng

Tìm hai số khi biết tổng và hiệu của hai số đó

Cách 1 :
Tìm số lớn = ( Tổng + hiệu ) : 2
Tìm số bé = số lớn – hiệu
hoặc số bé = tổng – số lớn
Cách 2 :
Tìm số bé = ( tổng – hiệu ) : 2
Tìm số lớn = số bé + hiệu
hoặc số lớn = tổng – số bé

Tìm hai số khi biết tổng và tỉ số của hai số đó

Cách làm :
Bước 1 : Tìm tổng số phần bằng nhau = Lấy số phần số lớn + số phần số bé
Bước 2 : Tìm số bé = Lấy tổng : tổng số phần bằng nhau × số phần số bé
Bước 3 : Tìm số lớn = lấy tổng – số bé

Tìm hai số khi biết hiệu và tỉ số của hai số đó

Cách làm :
Bước 1 : Tìm hiệu số phần bằng nhau = Lấy số phần số lớn – số phần số bé
Bước 2 : Tìm số bé = Lấy hiệu : hiệu số phần bằng nhau × số phần số bé
Bước : Tìm số lớn = Lấy hiệu + số bé

G. Toán tỉ lệ thuận

1. Khái niệm : Hai đại lượng tỉ lệ thuận khi đại lượng này tăng ( hoặc giảm ) bao nhiêu lần thì đại lượng kia cũng tăng ( hoặc giảm ) đi bấy nhiêu lần .
2. Bài toán mẫu : Một xe hơi trong hai giờ đi được 90 km. Hỏi trong 4 giờ xe hơi đó đi được bao nhiêu ki – lô – mét ?
Tóm tắt :
2 giờ : 90 km
4 giờ : … km ?
Bài giải
Cách 1 :
Trong một giờ xe hơi đi được là :
90 : 2 = 45 ( km ) ( * )
Trong 4 giờ xe hơi đi được là :
45 × 4 = 180 ( km )
Đáp số : 180 km
Cách 2 :
4 giờ gấp 2 giờ số lần là :
4 : 2 = 2 ( lần ) ( * * )
Trong 4 giờ xe hơi đi được là :
90 × 2 = 180 ( km )
Đáp số : 180 km
( * ) Bước này là bước “ rút về đơn vị chức năng ” ( * * ) Bước này là bước “ tìm tỉ số ”

H. Toán tỉ lệ nghịch

1. Khái niệm : Hai đại lượng tỉ lệ nghịch khi đại lượng này tăng ( hoặc giảm ) bao nhiêu lần thì đại lượng kia lại giảm ( hoặc tăng ) bấy nhiêu lần .
2. Bài toán mẫu : Muốn đắp xong nền nhà trong hai ngày, cần có 12 người. Hỏi muốn đắp xong nền nhà đó trong 4 ngày thì cần có bao nhiêu người ? ( Mức làm của mỗi người như nhau )
Tóm tắt :
2 ngày : 12 người
4 ngày : …. người ?
Bài giải
Cách 1 :
Muốn đắp xong nền nhà trong 1 ngày, cần số người là :
12 × 2 = 24 ( người ) ( * )
Muốn đắp xong nền nhà trong 4 ngày, cần số người là :
24 : 4 = 6 ( người )
Đáp số : 6 người
( * ) Bước này là bước “ rút về đơn vị chức năng ”
Cách 2 :
4 ngày gấp 2 ngày số lần là :
4 : 2 = 2 ( lần ) ( * * )
Muốn đắp xong nền nhà trong 4 ngày, cần số người là :
12 : 2 = 6 ( người )
Đáp số : 6 người
( * * ) Bước này là bước “ tìm tỉ số ”

I. Tìm phân số của một số

KL : muốn tìm phân số của một số ít, ta lấy số đó nhân với phân số đã cho .
Công thức tổng quát : giá trị a / b của A = A × a / b
VD : Trong rổ có 12 quả cam. Hỏi 2/3 số cam trong rổ là bao nhiêu ?
Giải
2/3 Số cam trong rổ là :
12 × 2/3 = 8 ( quả )
ĐS : 8 quả

K. Tìm một số biết giá trị phân số của số đó

KL : Muốn tìm một số ít khi biết một giá trị phân số của số đó, ta lấy giá trị đó chia cho phân số .
CTTQ :
Giá trị a / b của A = giá trị của phân số : a / b
VD : Cho 2/3 số cam trong rổ cam là 8 quả. Hỏi rổ cam đó có bao nhiêu quả ?
Giải
Số cam trong rổ là :
8 : 2/3 = 12 ( quả )
ĐS : 12 quả

L. Tỉ số phần trăm

1. Tìm tỉ số phần trăm của hai số: ta làm như sau:

– Tìm thương của hai số đó dưới dạng số thập phân .
– Nhân thương đó với 100 và viết thêm kí hiệu Xác Suất ( % ) vào bên phải tích tìm được .
CTTQ : a : b = T ( STP ) = STP × 100 ( % )
VD : Tìm tỉ số Tỷ Lệ của 315 và 600
Giải
Tỉ số Xác Suất của 315 và 600 là :
315 : 600 = 0,525 = 52,5 %
ĐS : 52,5 %

2. Tìm giá trị phần trăm của một số cho trước: ta lấy số đó chia cho 100 rồi nhân với số phần trăm hoặc lấy số đó nhân với số phần trăm rồi chia cho 100.

CTTQ : Giá trị % = Số A : 100 × số % hoặc Giá trị % = Số A × số % : 100
VD : Trường Đại Từ có 600 học viên. Số học sinh nữ chiếm 45 % số học viên toàn trường. Tính số học viên nữ của trường .
Giải
Số học sinh của trường đó là :
600 : 100 × 45 = 270 ( học viên )
ĐS : 270 học viên

3. Tìm một số biết giá trị phần trăm của số đó: ta lấy giá trị phần trăm của số đó chia cho số phần trăm rồi nhân với 100 hoặc ta lấy giá trị phần trăm của số đó nhân với 100 rồi chia cho số phần trăm.

CTTQ : Số A = Giá trị % : số Xác Suất × 100 hoặc Số A = Giá trị % × 100 : số Tỷ Lệ
VD : Tìm một số ít biết 30 % của nó bằng 72 .
Giải
Giá trị của số đó là :

72 : 30 × 100 = 240

ĐS : 240

M. Bảng đơn vị đo độ dài

1. Bảng đơn vị đo độ dài:

2. Nhận xét:

• Hai đơn vị đo độ dài liền nhau gấp (hoặc kém) nhau 10 lần.

VD : 1 m = 10 dm
1 cm = 1/10 dm = 0,1 dm

• Mỗi đơn vị đo độ dài ứng với một chữ số.

VD : 1245 m = 1 km 2 hm 4 dam 5 m

N. Bảng đơn vị đo khối lượng

1. Bảng đơn vị đo khối lượng:

2. Nhận xét:

• Hai đơn vị đo khối lượng liền nhau gấp (hoặc kém) nhau 10 lần.

VD : 1 kg = 10 hg
1 g = 1/10 dag = 0,1 dag

• Mỗi đơn vị đo khối lượng ứng với một chữ số.

VD : 1245 g = 1 kg 2 hg 4 dag 5 g

O. Bảng đơn vị đo diện tích

1. Bảng đơn vị đo diện tích:

2. Nhận xét:

• Hai đơn vị đo diện tích liền nhau gấp (hoặc kém) nhau 100 lần.

VD : 1 mét vuông = 100 dm2
1 cm2 = 1/100 dm2 = 0,01 dm2

• Mỗi đơn vị đo độ dài ứng với hai chữ số.

VD : 1245 mét vuông = 12 dam2 45 mét vuông

P. Bảng đơn vị đo thể tích

Mét khối	Đề – xi -mét khối	xăng- ti- mét khối
1m3	1dm3	1cm3
= 1000 dm3	= 1000 cm3
	= 1/1000 m3	= 1/1000 dm3
	= 0,001m3	= 0,001dm3

Nhận xét:

• Hai đơn vị đo thể tích liền nhau gấp (hoặc kém) nhau 1000 lần.

VD : 1 m3 = 1000 dm3
1 cm3 = 1/1000 dm3 = 0,001 dm3

• Mỗi đơn vị đo diện tích ứng với ba chữ số.
• VD: 1245dm3 = 1m3 245dm3

Lưu ý: 1dm3 = 1 l

R. HÌNH VUÔNG

1. Tính chất: Hình vuông là tứ giác có 4 góc vuông, 4 cạnh dài bằng nhau.

Cạnh kí hiệu là a

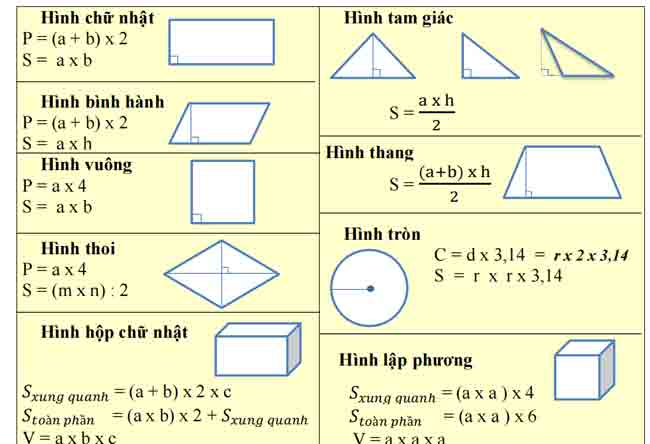
2.Tính chu vi: Muốn tính chu vi hình vuông, ta lấy số đo một cạnh nhân với 4.

CTTQ : P = a × 4
Muốn tìm một cạnh hình vuông vắn, ta lấy chu vi chia cho 4. a = P : 4

3. Tính diện tích: Muốn tính diện tích hình vuông, ta lấy số đo một cạnh nhân với chính nó.

CTTQ : S = a × a
· Muốn tìm 1 cạnh hình vuông vắn, ta tìm xem 1 số ít nào đó nhân với chính nó bằng diện tích quy hoạnh, thì đó là cạnh .
· VD : Cho diện tích quy hoạnh hình vuông vắn là 25 mét vuông. Tìm cạnh của hình vuông vắn đó .
Giải
Ta có 25 = 5 × 5 ; vậy cạnh hình vuông vắn là 5 m

S. HÌNH CHỮ NHẬT

1. Tính chất: Hình chữ nhật là tứ giác có 4 góc vuông, 2 chiều dài bằng nhau, 2 chiều rộng bằng nhau.

Kí hiệu chiều dài là a, chiều rộng là b

2. Tính chu vi: Muốn tính chu vi hình chữ nhật, ta lấy số đo chiều dài cộng số đo chiều rộng

( cùng đơn vị chức năng đo ) rồi nhân với 2 .
CTTQ : P = ( a + b ) × 2
* Muốn tìm chiều dài, ta lấy chu vi chia cho 2 rồi trừ đi chiều rộng a = P : 2 – b
· Muốn tìm chiều rộng, ta lấy chu vi chia cho 2 rồi trừ đi chiều dài .
b = P : 2 – a

3. Tính diện tích: Muốn tính diện tích hình chữ nhật, ta lấy số đo chiều dài nhân với số đo chiều rộng (cùng đơn vị đo).

CTTQ : S = a × b
· Muốn tìm chiều dài, ta lấy diện tích quy hoạnh chia cho chiều rộng. a = S : b
· Muốn tìm chiều rộng, ta lấy diện tích quy hoạnh chia cho chiều dài .
b = S : a

T. Hình bình hành

Tính chất: Hình bình hành có hai cặp

cạnh đối lập song song và bằng nhau .

Kí hiệu: Đáy là a,

chiều cao là h

Tính chu vi: Chu vi hình bình hành là tổng độ dài của 4 cạnh

Tính diện tích: Muốn tính diện tích hình bình hành, ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo)

CTTQ: S = a × h

– Muốn tìm độ dài đáy, ta lấy diện tích chia cho chiều cao.

a = S : b

– Muốn tìm chiều rộng, ta lấy diện tích chia cho chiều dài.

b = S : a

U. Hình thoi

Tính chất:

Hình thoi có hai cặp cạnh đối lập song song và bốn cạnh bằng nhau
Hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường .

Kí hiệu hai đường chéo là m và n

Tính chu vi: Muốn tính chu vi hình thoi, ta lấy số đo một cạnh nhân với 4.

Tính diện tích: Diện tích hình thoi bằng tích của độ dài hai đường chéo chia cho 2 (cùng đơn vị đo).

V. Hình thang

Tính chất: Hình thang có một cặp cạnh đối diện song song.

– Chiều cao: là đoạn thẳng ở giữa hai đáy và vuông góc với hai đáy.

Kí hiệu: đáy lớn là a, đáy nhỏ là b, chiều cao là h

Tính diện tích: Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho 2.

S = (a + b) × h : 2

Hoặc: Muốn tính diện tích hình thang ta lấy trung bình cộng hai đáy nhân với chiều cao.

S = × h

– Tính tổng hai đáy: Ta lấy diện tích nhân với 2 rồi chia cho chiều cao.

(a + b) = S × 2 : h

– Tính trung bình cộng hai đáy: Ta lấy diện tích chia cho chiều cao.

= S : h

– Tính độ dài đáy lớn: Ta lấy diện tích nhân với 2, chia cho chiều cao rồi trừ đi độ dài đáy bé.

a = S × 2 : h – b

– Tính độ dài đáy bé: Ta lấy diện tích nhân với 2, chia cho chiều cao rồi trừ đi độ dài đáy lớn.

b = S × 2 : h – a

– Tính chiều cao: Ta lấy diện tích nhân với 2 rồi chia cho tổng độ dài hai đáy.

h = S × 2 : (a + b)

hoặc: Tính chiều cao: Ta lấy diện tích chia cho trung bình cộng của hai đáy.

X. Hình tam giác

Tính chất: Hình tam giác có ba cạnh, 3 góc, 3 đỉnh.

Chiều cao là đoạn thẳng hạ từ đỉnh vuông góc với cạnh đối lập .

Kí hiệu đáy là a, chiều cao là h

Tính chu vi: Chu vi hình tam giác là tổng độ dài của 3 cạnh.

Tính diện tích: Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho 2.

S = a × h : 2

– Tính cạnh đáy: Ta lấy diện tích nhân với 2 rồi chia cho chiều cao.

a = S × 2 : h

– Tính chiều cao: Ta lấy diện tích nhân với 2 rồi chia cho cạnh đáy.

h = S × 2 : a

Y. Hình tròn

1. Tính chất: Hình tròn có tất cả các bán kính bằng nhau.

– Đường bao quanh hình tròn trụ gọi là đường tròn .
– Điểm chính giữa hình tròn trụ là tâm .

– Đoạn thẳng nối tâm với một điểm trên đường tròn gọi là bán kính. Ki hiệu là r

– Đoạn thẳng đi qua tâm và nối hai điểm của đường tròn gọi là đường kính .

Đường kính gấp hai lần bán kính. Kí hiệu là d

2. Tính chu vi: Muốn tính chu vi hình tròn ta lấy đường kính nhân với số 3,14.

C = d × 3,14

Hoặc ta lấy nửa đường kính nhân 2 rồi nhân với số 3,14 .

C = r × 2 × 3,14

Tính đường kính : ta lấy chu vi chia cho số 3,14

d = C : 3,14

Tính nửa đường kính : ta lấy chu vi chia cho 2 rồi chia cho số 3,14

r = C : 2 : 3,14 (Tính ra nháp: r = C : 6,28)

3. Tính diện tích: Muốn tính diện tích hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số 3,14. S = r × r × 3,14

– Biết diện tích, muốn tìm bán kính, ta làm như sau: Lấy diện tích chia cho số 3,14 để tìm tích của hai bán kính rồi tìm xem số nào đó nhân với chính nó bằng tích đó thì đấy là bán kính hình tròn.

VD : Cho diện tích quy hoạnh một hình tròn trụ bằng 28,26 cm2. Tìm nửa đường kính hình tròn trụ đó .
Giải
Tích hai nửa đường kính hình tròn trụ là :
28,26 : 3,14 = 9 ( cm2 )
Vì 9 = 3 × 3 nên nửa đường kính hình tròn trụ là 3 cm

Hình hộp chữ nhật

1. Tính chất: Hình hộp chữ nhật có 6 mặt, hai mặt đáy và bốn mặt bên.

– Có 8 đỉnh, 12 cạnh

– Có ba kích thước: chiều dài (a), chiều rộng (b), chiều cao (c).

2. Tính diện tích xung quanh: Muốn tính diện tích xung quanh hình hộp chữ nhật ta lấy chu vi đáy nhân với chiều cao (cùng một đơn vị đo).

S×q = P(đáy) × c

Hoặc: S×q = (a + b) × 2 × c

– Muốn tìm chu vi đáy, ta lấy diện tích xung quanh chia cho chiều cao.

P (đáy) = S×q : c

– Muốn tìm chiều cao, ta lấy diện tích xung quanh chia cho chu vi đáy

c = S×q : P (đáy)

– Muốn tìm tổng hai đáy, ta lấy diện tích xung quanh chia cho 2 rồi chia cho chiều cao.

(a + b) = S×q : 2 : h

– Muốn tìm chiều dài, ta lấy diện tích xung quanh chia cho 2, chia cho chiều cao rồi trừ đi chiều rộng.

a = S×q : 2 : c – b

– Muốn tìm chiều rộng, ta lấy diện tích xung quanh chia cho 2, chia cho chiều cao rồi trừ đi chiều dài.

b = S×q : 2 : c – a

– Tính diện tích toàn phần: Muốn tính diện tích toàn phần hình hộp chữ nhật ta lấy diện tích xung quanh cộng diện tích hai đáy.

Stp = S×q + S (2đáy)

Hoặc: Stp = (a + b ) × 2 × c + a × b × 2

– Muốn tìm diện tích đáy ta lấy chiều dài nhân với chiều rộng.

S(đáy) = a × b

– Muốn tìm chiều dài, ta lấy diện tích đáy chia cho chiều rộng.

a = S(đáy) : b

– Muốn tìm chiều rộng, ta lấy diện tích đáy chia cho chiều dài.

b = S (đáy) : a

4. Tính thể tích hình hộp chữ nhật: ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo).

V = a × b × c

– Muốn tìm chiều dài, ta lấy thể tích chia cho chiều rộng rồi chia tiếp cho chiều cao.

a = V : b : c

– Muốn tìm chiều rộng, ta lấy thể tích chia cho chiều dài rồi chia tiếp cho chiều cao.

b = V : a : c

– Muốn tìm chiều cao, ta lấy thể tích chia cho chiều dài rồi chia tiếp cho chiều rộng.

c = V : a : b

hoặc lấy thể tích chia cho diện tích quy hoạnh đáy

c = V : S(đáy)

Hình lập phương

1. Tính chất: Hình lập phương có 6 mặt là các hình vuông bằng nhau.

– Có 8 đỉnh, 12 cạnh dài bằng nhau. Kí hiệu cạnh là a

2. Tính diện tích ×ung quanh: Muốn tính diện tích ×ung quanh hình lập phương ta lấy

diện tích một mặt nhân với 4: S×q = S(1 mặt) × 4

3. Tính diện tích toàn phần: Muốn tính diện tích toàn phần hình lập phương ta lấy diện tích một mặt nhân với 6: Stp = S(1 mặt) × 6

Muốn tìm diện tích một mặt ta lấy diện tích ×ung quanh chia cho 4 hoặc diện tích toàn phần chia cho 6.

S(1 mặt) = S×q : 4

Hoặc: S(1 mặt) = Stp : 6

– Muốn tìm 1 cạnh hình lập phương, ta tìm xem một số nào đó nhân với chính nó bằng diện tích một mặt, thì đó là cạnh.

– VD: Cho diện tích một mặt là 25 m2. Tìm cạnh của hình lập phương đó.

Giải
Ta có 25 = 5 × 5 ;
vậy cạnh hình lập phương là 5 m

4.Tính thể tích hình lập phương: ta lấy cạnh nhân với cạnh rồi nhân với cạnh.

V = a × a × a

Muốn tìm 1 cạnh hình lập phương, ta tìm xem một số nào đó nhân với chính nó rồi nhân tiếp với nó bằng thể tích, thì đó là cạnh.

VD : Cho thể tích là 125 mét vuông. Tìm cạnh của hình lập phương đó .
Giải
Ta có 25 = 5 × 5 × 5 ; Vậy cạnh hình lập phương là 5 m

Toán chuyển động

I. Có một động tử chuyển động

1. Vận tốc : Muốn tính tốc độ ta lấy quãng đường chia cho thời hạn .
v = s : t
2. Quãng đường : Muốn tính quãng đường ta lấy tốc độ nhân với thời hạn .
s = v × t
3. Thời gian : Muốn tính thời hạn ta lấy quãng đường chia cho tốc độ
t = s : v

II. Có hai động tử cùng chuyển động

1. Cùng xuất phát đi ngược chiều để gặp nhau:

a, Tìm tổng tốc độ của hai hoạt động :
( v1 + v2 ) = s : t
b, Tìm quãng đường của hai hoạt động :
s = ( v1 + v2 ) × t
c, Tìm thời hạn của hai hoạt động :
t = s : ( v1 + v2 )

2. Cùng xuất phát đi cùng chiều để gặp nhau:

a, Tìm hiệu vận tốc của hai chuyển động: (v1 – v2) = s : t

b, Tìm quãng đường của hai hoạt động : s = ( v1 – v2 ) × t
c, Tìm thời hạn của hai hoạt động : t = s : ( v1 – v2 )

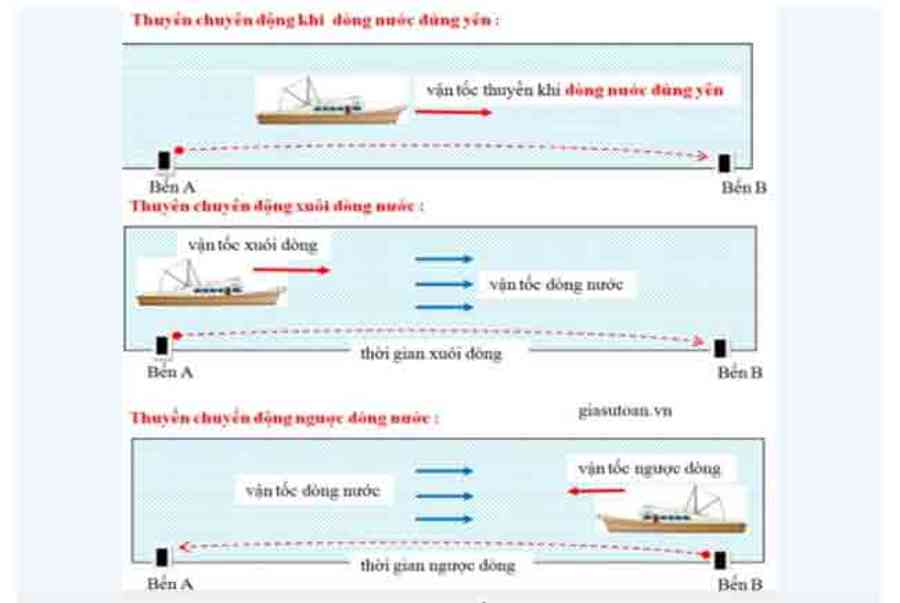
III. Chuyển động dưới nước

1. Chuyển động xuôi dòng:

a. Tìm tốc độ xuôi dòng :
v × uôi = vthuyền + vnước = s : t
b. Tìm quãng đường :
s = ( vthuyền + vnước ) × t
c. Tìm thời hạn :
t = s : ( vthuyền + vnước )
2. Chuyển động ngược dòng :
a. Tìm tốc độ ngược dòng :
Vngược = vthuyền – vnước = s : t

b. Tìm quãng đường:

s = ( vthuyền – vnước ) × t
c. Tìm thời hạn :
t = s : ( vthuyền – vnước )