Nội dung chính
- 1 Công thức tính thể tích khối chóp cực hay (tam giác đều, tứ giác, …)
- 1.1 Công thức tính thể tích khối chóp cực hay (tam giác đều, tứ giác, …)
- 1.1.1 Tính thể tích khối chóp có hình chiếu vuông góc của đỉnh lên mặt đáy
- 1.1.2 A. Phương pháp giải & Ví dụ
- 1.1.3 Ví dụ minh họa
- 1.1.4 Tính thể tích khối chóp có mặt bên vuông góc với đáy
- 1.1.5 A. Phương pháp giải & Ví dụ
- 1.1.6 Ví dụ minh họa
- 1.1.7 Ngân hàng trắc nghiệm miễn phí ôn thi THPT Quốc Gia tại khoahoc.vietjack.com
- 1.1.8 Share this:
- 1.1 Công thức tính thể tích khối chóp cực hay (tam giác đều, tứ giác, …)
Công thức tính thể tích khối chóp cực hay (tam giác đều, tứ giác, …)
Công thức tính thể tích khối chóp cực hay (tam giác đều, tứ giác, …)
Bài giảng: Cách tính Thể tích hình chóp, hình lăng trụ – Cô Nguyễn Phương Anh (Giáo viên VietJack)
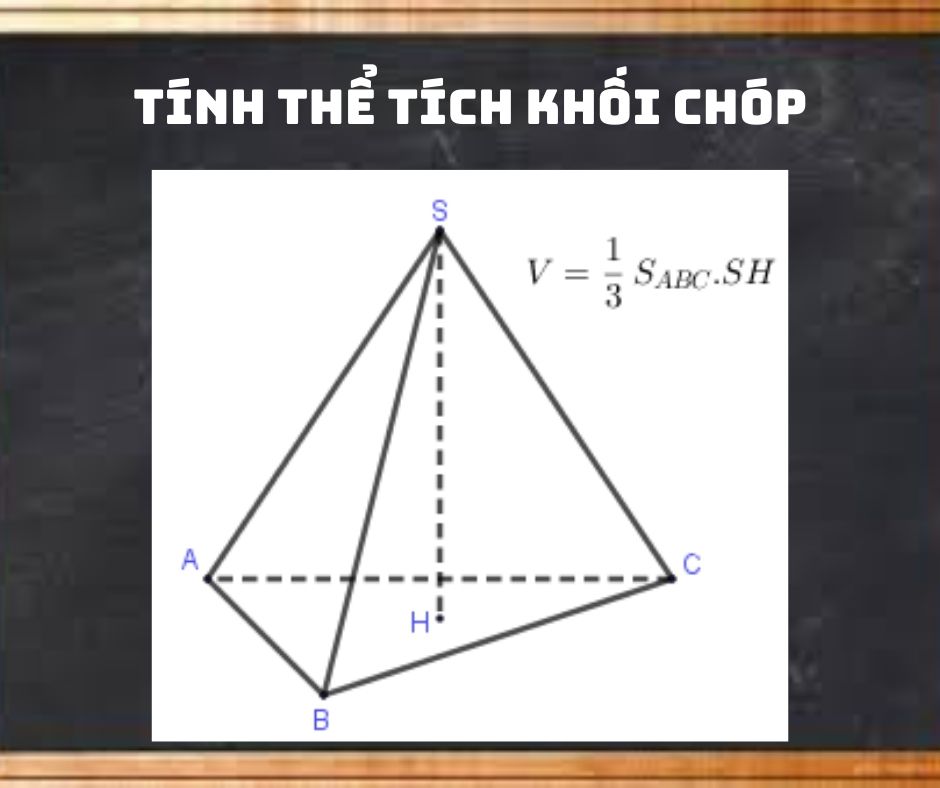
* Nếu khối chóp đã cho có chiều cao h và diện tích đáy Sday thì thể tích tính theo công thức:
* Để xác định được chiều cao của hình chóp ta cần xác định:
• Chóp có cạnh bên vuông góc chiều cao chính là cạnh bên .• Chóp có hai mặt bên vuông góc đáy đường cao là giao tuyến của hai mặt bên vuông góc đáy .• Chóp có mặt bên vuông góc đáy chiều cao của mặt bên vuông góc đáy .• Chóp đều chiều cao hạ từ đỉnh đến tâm đa giác đáy .• Chóp có hình chiếu vuông góc của một đỉnhlên xuống mặt dưới thuộc cạnh dưới mặt đáy đường cao là từ đỉnh tới hình chiếu .
Quảng cáo
Chú ý: Các công thức tính diện tích đa giác
a ) Tam giác :
b ) Hình vuông cạnh a : S = a2 ( a : cạnh hình vuông vắn )c ) Hình chữ nhật : S = a. b ( a, b : hai kích cỡ )
d) Hình bình hành ABCD: S = đáy x cao = AB. AD.
e) Hình thoi ABCD: S= AB. AD.
f) Hình thang:
g) Tứ giác ABCD có hai đường chéo vuông góc:
Quảng cáo
Tính thể tích khối chóp có hình chiếu vuông góc của đỉnh lên mặt đáy
A. Phương pháp giải & Ví dụ
1. Định nghĩa: Một hình chóp được gọi là hình chóp đều nếu đáy của nó là một đa giác đều và các cạnh bên bằng nhau.
2. Kết quả: Trong hình chóp đều:
+ Đường cao hình chóp qua tâm của đa giác đáy .
+ Các cạnh bên tạo với đáy những góc bằng nhau .
+ Cắt mặt bên tạo với đáy những góc bằng nhau .
Ví dụ minh họa
Bài 1: Cho khối chóp S.ABCD có ABCD là hình chữ nhật, AD = 2a, AB = a. Gọi H là trung điểm AD, biết SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết SA=a√5
Hướng dẫn:
Quảng cáo
Xem thêm: Tam giác.
Bài 2: Cho khối chóp S.ABC có tam giác ABC vuông tại B, AB = 3a, AC = 6a. Hình chiếu của S trên mặt phẳng (ABC) là điểm H thuộc đoạn AB sao cho AH = 2HB. Biết SC hợp với (ABC) một góc bằng 60º . Tính thể tích khối chóp S.ABC
Hướng dẫn:
Tam giác ABC vuông tại B, AB = 3 a, AC = 6 a
AH = 2HB ; AB = 3 a ⇒ HB = a
Có : SH ⊥ ( ABCD ) nên góc giữa SC và ( ABC ) là góc giữa SC và HC
Bài 3: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = a, BC=a√3, H là trung điểm của cạnh AD. Biết hai mặt phẳng (SHC) và (SHD) cùng vuông góc với mặt đáy, đường thẳng SD tạo với đáy một góc 60º. Tính thể tích của khối chóp theo a
Hướng dẫn:
HD là hình chiếu vuông góc của SD lên mặt phẳng ( ABCD ). Do đó góc giữa đường thẳng SD và đáy là góc giữa HD và SD
Tính thể tích khối chóp có mặt bên vuông góc với đáy
A. Phương pháp giải & Ví dụ
Để xác lập đường cao hình chóp, ta vận dụng định lí sau :
Ví dụ minh họa
Bài 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BA = 3a, BC = 4a; mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết SB=2a√3 và ∠(SBC)=30º. Tính thể tích khối chóp S.ABC
Kẻ SH vuông góc với BC
Xét tam giác Ngân hàng Sài Gòn Hà Nội SHB vuông tại H có :
Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh a. Mặt bên (SAB) là tam giác đều nằm trong mặt phẳng vuông góc với đáy ABCD. Tính thể tích khối chóp S.ABCD
Gọi H là trung điểm của AB
∆ SAB đều nên SH ⊥ AB
( SAB ) ⊥ ( ABCD ) ⇒ SH ⊥ ( ABCD )
Vậy H là chân đường cao của khối chóp .
Ta có : ∆ SAB đều cạnh a nên SH = a √ 3/2
Bài 3: Cho tứ diện ABCD có ABC là tam giác đều, BCD là tam giác vuông cân tại D. (ABC) ⊥ (BCD) và AD hợp với (BCD) một góc 60º, AD = a. Tính thể tích của tứ diện ABCD
Gọi H là trung điểm của BC. Ta có tam giác ABC đều nên AH ⊥ BC
Ta có : HD là hình chiếu vuông góc của DA lên mặt phẳng ( BCD )
Do đó, góc giữa HD và mặt phẳng ( BCD ) là góc giữa AD và DH
⇒ ∠ ( ADH ) = 60 º
Xét tam giác AHD vuông tại H có :
BCD là tam giác vuông cân tại D có DH là trung tuyến nên
BC = 2DH = a
Bài 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, gọi M là trung điểm của AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy (ABCD), biết SD=2a√5, SC tạo với mặt đáy (ABCD) một góc 60º. Tính theo a thể tích của khối chóp S.ABCD
Tam giác SAB cân tại S có M là trung điểm của AB nên SM ⊥ AB
MC là hình chiếu vuông góc của SC lên mặt phẳng ( ABCD ) nên góc giữa SC và mặt phẳng ( ABCD ) là góc giữa SC và MC
⇒ ∠ ( SCM ) = 60 º
Trong tam giác vuông SMC và SMD có :
Do ABCD là hình vuông vắn nên MC = MD
Lại có :
Xem thêm các dạng bài tập Toán lớp 12 có trong đề thi THPT Quốc gia khác:
Xem thêm: Cách chứng minh đường trung trực lớp 7
Giới thiệu kênh Youtube VietJack
Ngân hàng trắc nghiệm miễn phí ôn thi THPT Quốc Gia tại khoahoc.vietjack.com
khoi-da-dien.jsp
Source: http://139.180.218.5
Category: tản mạn