Nội dung chính
I. KHỐI NÓN LÀ HÌNH GÌ?
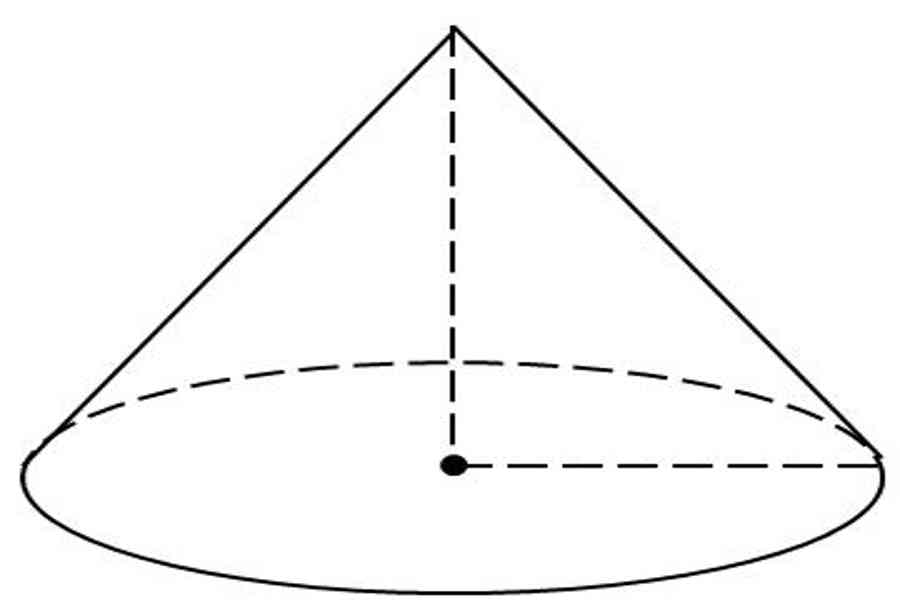
Trong hình học khoảng trống, khi xoay một tam giác vuông quanh trục của nó ( một cạnh góc vuông ) một vòng ta được hình tròn trụ nón .Ví dụ : Khối nón .
II. DIỆN TÍCH KHỐI NÓN
Công thức tính diện tích xung quanh khối nón bằng tích pi bán kính mặt cầu đáy với độ dài đường sinh khối nón, như sau:
\(S_{xq}=\pi rl\)
Trong đó:
- \(S_{xq}\): diện tích xung quanh khối nón.
- r: độ dài bán kính mặt cầu đáy.
- h: độ dài chiều cao nối từ đáy tới đỉnh khối nón.
- l: độ dài đường sinh của khối nón.
Công thức tính diện tích toàn phần khối nón bằng tổng diện tích xung quanh và diện tích đáy khối nón, như sau:
\(S_{tp}=S_{xq}+S_{d} \\ =\pi rl+\pi r^2\)
Trong đó :
- S: diện tích toàn phần khối nón.
- r: độ dài bán kính mặt cầu đáy.
- h: độ dài chiều cao nối từ đáy tới đỉnh khối nón.
- l: độ dài đường sinh của khối nón.
III. THỂ TÍCH KHỐI NÓN
Công thức tính thể tích khối nón bằng 1/3 pi chiều cao hình nón với bình phương nửa đường kính mặt cầu đáy, như sau :
\(V=\dfrac{\pi r^2 h}{3}\)
Trong đó :
- V: thể tích khối nón.
- r: độ dài bán kính mặt cầu đáy.
- h: độ dài chiều cao nối từ đáy tới đỉnh khối nón.
IV. BÀI TẬP THAM KHẢO DIỆN TÍCH VÀ THỂ TÍCH KHỐI NÓN
Ví dụ: Tính thể tích và diện tích toàn phần của khối nón biết bán kính mặt cầu đáy dài 6m và độ dài chiều cao nối từ đáy tới đỉnh khối nón là 8m.
Lời giải tham khảo:
Áp dụng công thức Pitago, đường sinh của khối nón là :\ ( l = \ sqrt { r ^ 2 + h ^ 2 } \ \ = \ sqrt { 6 ^ 2 + 8 ^ 2 } = 10 ( m ) \ )
Áp dụng công thức tính thể tích của khối nón, ta có thể tích của khối nón đã cho là:
\ ( V = \ dfrac { \ pi r ^ 2 h } { 3 } \ \ = \ dfrac { \ pi. 6 ^ 2. 8 } { 3 } = 96 \ pi ( m ^ 3 ) \ )Áp dụng công thức tính diện tích quy hoạnh toàn phần khối nón, ta có diện tích quy hoạnh toàn phần khối nón đã cho là :\ ( S_ { tp } = S_ { xq } + S_ { d } = \ pi rl + \ pi r ^ 2 \ \ = ( 6.10 + 6 ^ 2 ). \ pi = 96 \ pi ( m ^ 2 ) \ )
Source: http://139.180.218.5
Category: tản mạn