Công Thức Tính Diện Tích Hình Tứ Giác Lớp 3, Cách Tính Diện Tích Tứ Giác, Công Thức Tính

Bài viết sẽ chia sẻ đến bản những kiến thức về công thức và cách tính diện tích hình chữ nhật và chu vi chữ nhật kèm theo bài tập cơ bản áp dụng giúp các em học sinh hiểu rõ hơn về Hình Chữ Nhật.

Đang xem : Công thức tính diện tích hình tứ giác lớp 3
I. Hình Chữ Nhật và Các Dấu Hiệu Nhất BiếtII. Công Thức Tính Diện Tích Hình Chữ Nhật và Chu Vi Chữ Nhật

I. Hình Chữ Nhật và Các Dấu Hiệu Nhất Biết

Trong hình học phảng mà những em được học từ lớp 3, lớp 5 và những lớp lớn hơn thì cách tính chu vi, diện tích hình tròn trụ, hình vuông vắn, hình tam giác, hình bình hành, hình thang …. là những hình cơ bản nhất mà những em phải học. Đây là kiến thức và kỹ năng cơ bản nhất mà những em cần ghi nhớ để học những lớp cao hơn hay những việc làm phong cách thiết kế từ đơn thuần đến phức tạp

Trong bài viết này sẽ chia sẻ tới các em công thức tính chu vi hình chữ nhật và diện tích hình chữ nhật một cách chính xác, đơn giản và dễ hiểu nhất. Ngoài ra, các bạn muốn tìm gia sư Toán dạy kèm tại nhà giúp các con học tốt hơn hay tham khảo thêm nhiều kiến thức hay nữa tại đây nhé!

1. Định nghĩa và tính chất của hình chữ nhật

– Hình chữ nhật là một hình tứ giác có cả 4 góc đều là góc vuông và có 2 cặp cạnh song song nhau, hình chữ nhật là 1 hình tứ giác đặc biệt quan trọng
– hình chữ nhật cũng là một hình bình hành và là một hình thang cân. Vì thế, hình chữ nhật có toàn bộ những đặc thù của 2 hình trên
– Trong hình chữ nhật thì 2 đường chéo có độ dài bằng nhau và cắt nhau tại trung điểm của mỗi đường .
– Hai đường chéo cắt nhau và chia hình bình hành thành 4 tam giác cân

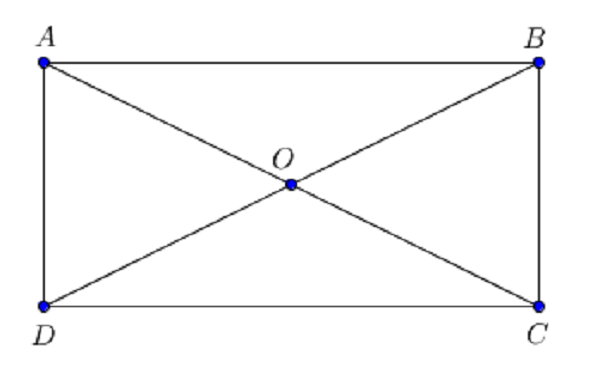
ABCD là hình chữ nhật ABCD là tứ giác có những góc A = B = C = D

2. Các diếu hiệu nhật biết hình chữ nhật

Hình chữ nhật là hình học những em sẽ được học khá nhiều và có rất nhiều ứng dụng trong trong thực tiễn. Hình chữ nhật có 4 tín hiệu phân biệt như sau :
– Là một hình bình hành có 1 góc vuông
– Là hình bình hành có 2 đường chéo dài bằng nhau
– Là hình thang cân có tối thiểu 1 góc vuông
– Là một tứ giác có 3 góc vuông

II. Công Thức Tính Diện Tích Hình Chữ Nhật và Chu Vi Chữ Nhật

Công thức tính chu vi và diện tích của hình chữ nhật là hai công thức khởi điểm khi những em mở màn học về hình học. Nó cũng là 2 chỉ số cơ bản và quan trọng đi theo những em trong suốt quy trình học do đó những em phải ghi nhớ hai công thức này .
Xem thêm : tính diện tích hình chữ nhật có chiều dài là 13 cm chiều rộng là 9 cm

1. Công thức tính chu vi hình chữ nhật

– Khái niệm : Chu vi của hình chữ nhật bằng tổng giá trị chiều và chiều rộng nhân với 2

( hoặc : chu vi của hình chữ nhật bằng hai lần giá trị của tổng chiều dài và chiều rộng của hình )

– Công thức tính chu vi :

Chu vi hình chữ nhật P = (A + B) X 2

– Ký hiệu :
+ P. là chu vi
+ A là chiều dài
+ B là chiều rộng

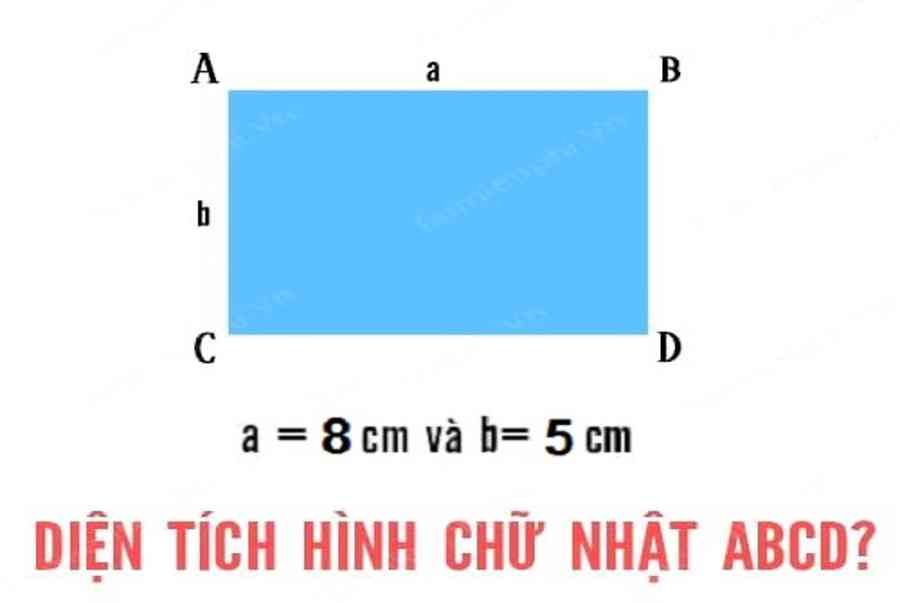
– Bài tập ví dụ : Cho hình chữ nhật ABCD có chiều dài AB là 8cm, chiều rộng BD là 5cm. Hãy tính chu vi của hình chữ nhật ABCD

Bài giải : vận dụng công thức tính chu vi của hình chữ nhật ta có :
P. = ( AB + BD ) X 2 = ( 8 + 5 ) X 2 = 26 cm

2. Công thức tính diện tích hình chữ nhật

– Khái niệm : Diện tích hình chữ nhật được tính bằng tích của chiều dài nhân với chiều rộng của hình

– Công thức tính diện tích :

Diện tích hình chữ nhật S = A X B
– Ký hiệu :
+ S là diện tích
+ A là chiều dài của hình
+ B là chiều rộng của hình

– Bài tập ví dụ : Cho hình chữ nhật ABCD có chiều dài AB là 8cm, chiều rộng BD là 5cm. Hãy tính diện tích của hình chữ nhật ABCD đó.

Xem thêm : Bài Tập Thì Hiện Tại Tiếp Diễn Cho Học Sinh Tiểu Học, Bài Tập Tiếng Anh Lớp 5 Thì Hiện Tại Tiếp Diễn
Bài giải : vận dụng công thức tính điện tích của hình chữ nhật ta có :

P = AB X BD = 8 X 5 = 30cm

III. Bài Tập Về Liên Quan Đến Diện Tích và Chu Vi Hình Chữ Nhật

Sau đây là một số bài tập áp dụng cho những kiến thức về chu vi hình chữ nhật và diện tích hình chữ nhật ở trên. Có rất nhiều ví dụ nhưng bài viết sẽ đưa ra những ví dụng điển hình nhất giúp các em học sinh tiếp cận được các dạng bài tập.

Xem thêm bài viết thuộc chuyên mục: Diện tích

Điều hướng bài viết