Dưới đây ThuThuatPhanMem. vn nhắc lại những kiến thức và kỹ năng về hình nón, công thức và cách tính diện tích quy hoạnh xung quanh hình nón, mời những bạn cùng theo dõi .

Hình nón là gì?

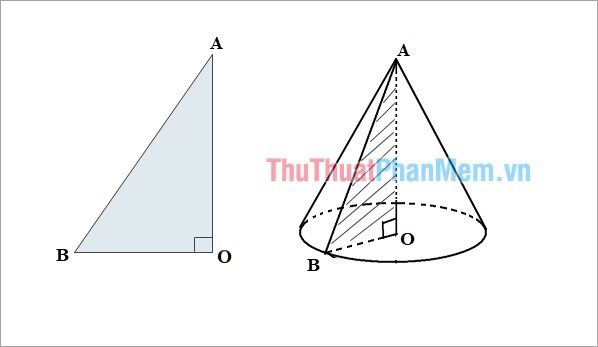
Khi ta quay tam giác vuông OAB một vòng quanh cạnh góc vuông OA cố định thì ta được hình nón. Như vậy hình nón được tạo bởi:

• Cạnh OB tạo nên đáy hình nón là một đường tròn tâm O.
• Cạnh AB quét lên mặt xung quanh của hình nón, mỗi vị trí của nó được gọi là một đường sinh.
• A là đỉnh của hình nón và AO là đường cao của hình nón.

Công thức tính diện tích xung quanh hình nón

Giả sử ta có hình nón như sau :

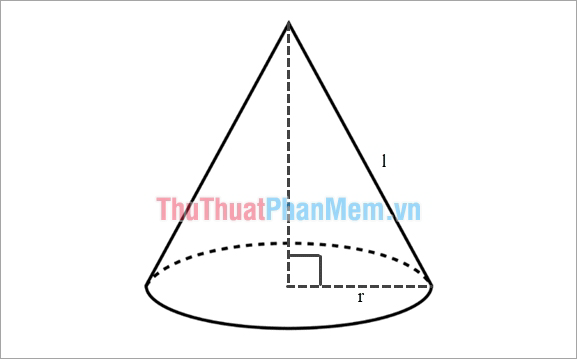
Diện tích xung quanh của hình nón được tính bằng công thức :
\ ( { S_ { xq } } = \ pi rl \ )
Trong đó :

• \({S_{xq}}\) là diện tích xung quanh của hình nón.
• \(\pi \) là hằng số (=3.14159265359)
• r là bán kính mặt đáy của hình nón.
• l là độ dài đường sinh của hình nón.

Cách tính diện tích xung quanh hình nón

Theo công thức tính diện tích quy hoạnh xung quanh hình nón thì để tính diện tích quy hoạnh xung quanh hình nón những bạn cần biết nửa đường kính mặt đất hình nón và độ dài đường sinh của hình nón .

Đầu tiên các bạn cần tính bán kính r mặt đáy hình nón nếu chưa biết.

Tiếp theo những bạn tính độ dài đường sinh l của hình nón nếu chưa biết .
Sau khi đã biết r và l những bạn vận dụng công thức \ ( { S_ { xq } } = \ pi rl \ ) để tính diện tích quy hoạnh xung quanh hình nón .

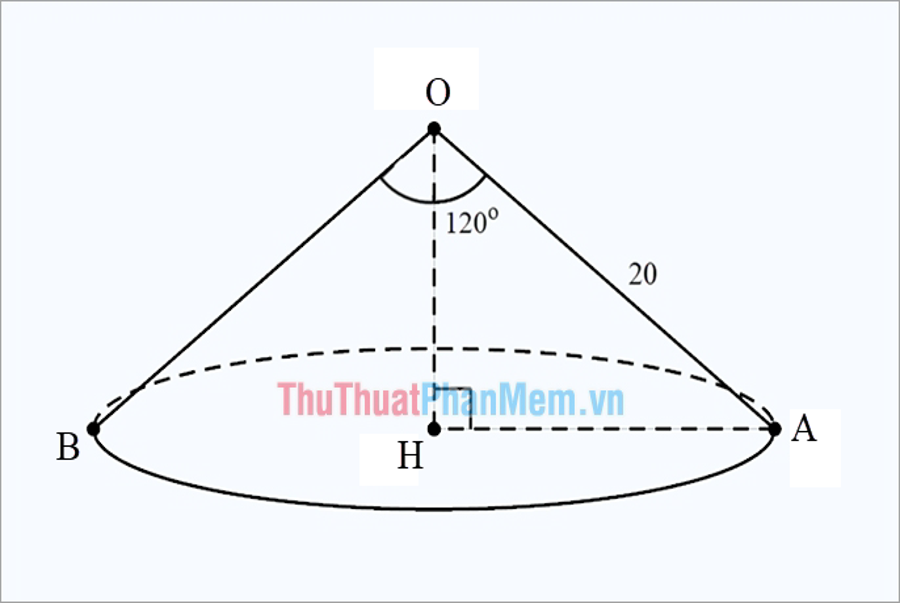
Ví dụ: Cho hình nón có góc ở đỉnh là \({120^ \circ }\), độ dài đường sinh là 20 cm, tính diện tích xung quanh của hình nón.

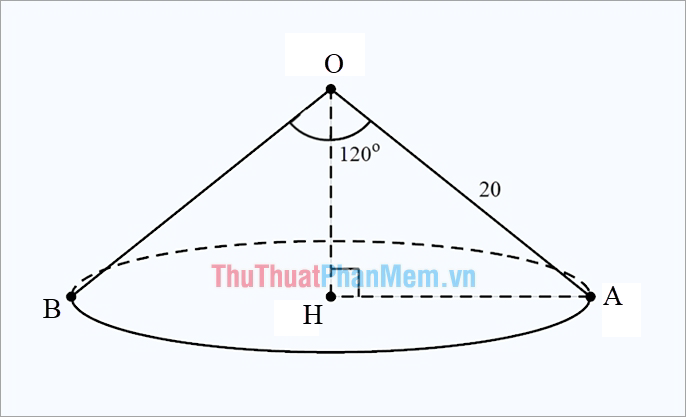
Gọi đỉnh hình nón là O, tâm đáy là H. Kẻ đường thằng đi qua tâm đáy AB ( đường kính đáy ) .
Như vậy \ ( \ widehat { AOB } \ ) = \ ( { 120 ^ \ circ } \ ) \ ( \ Rightarrow \ ) \ ( \ widehat { AOH } \ ) = \ ( { 60 ^ \ circ } \ ), OA = OB = 20 .

Trong tam giác OHA: r = HA = OA.sin ⁡\(\widehat {AOH}\) = 20.sin ⁡\({60^ \circ }\) = 20.\(\frac{{\sqrt 3 }}{2}\) = 10\(\sqrt 3 \)

\ ( \ Rightarrow \ ) Diện tích xung quanh của hình nón là :
\ ( { S_ { xq } } = \ pi rl = \ pi. 10 \ sqrt 3. 20 = 200 \ sqrt 3 \ pi ( c { m ^ 2 } ) \ )
Như vậy trên đây ThuThuatPhanMem. vn đã san sẻ đến những bạn công thức, cách tính và ví dụ cụ thể cách tính diện tích quy hoạnh xung quanh hình nón. Hi vọng qua bài viết này những bạn sẽ nhớ lại công thức và cách tính diện tích quy hoạnh xung quanh hình nón .

Source: http://139.180.218.5
Category: tản mạn