Điều kiện cần và đủ là gì? Mệnh đề điều kiện cần, điều kiện đủ?

Điều kiện cần và đủ ( Necessary and sufficient conditions ) là gì ? Điều kiện cần và đủ tiếng anh là gì ? Mệnh đề điều kiện cần, điều kiện đủ ?

Cách phát hiện điều kiện cần và đủ là một nội dung rất quan trọng, sẽ giúp học viên nắm được Cách phát biểu mệnh đề điều kiện cần và đủ hay, cụ thể. Vậy làm thế nào để hoàn toàn có thể phát hiện Mệnh đề điều kiện cần, điều kiện đủ. Bài viết dưới đây chúng tôi sẽ làm rõ cho bạn đọc hiểu hơn về điều kiện cần và đủ là gì ? Mệnh đề điều kiện cần, điều kiện đủ ? Hi vọng những thông tin dưới đây sẽ hữu dụng với bạn đọc.

Luật sư tư vấn pháp luật trực tuyến qua tổng đài: 1900.6568

1. Điều kiện cần và đủ là gì?

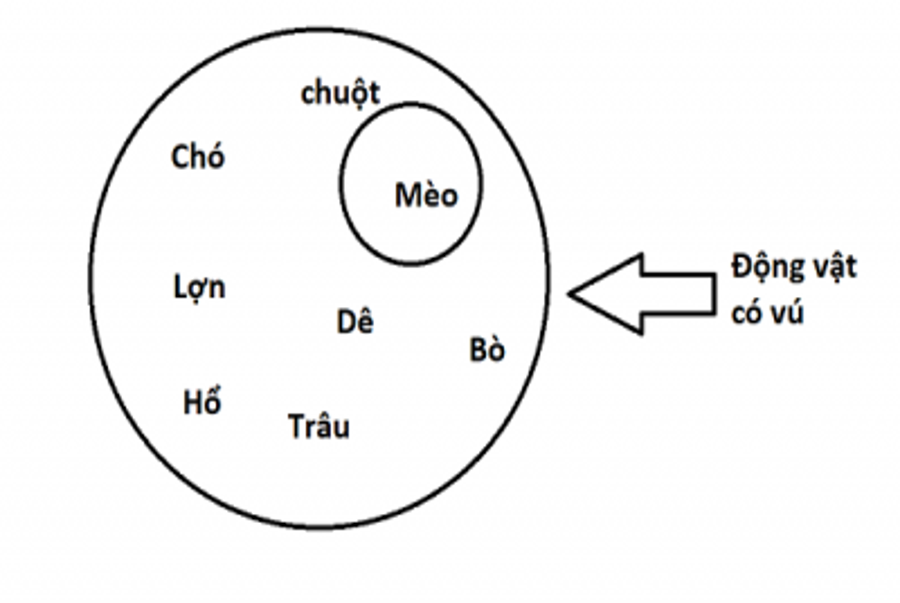
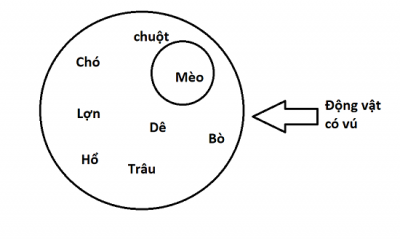
Điều kiện là sự kiện hoàn toàn có thể xảy ra và không chắc như đinh phải xảy ra. Về góc nhìn hợp đồng xác lập một sự kiện và khi sự kiện đó xảy ra thì hợp đồng phát sinh hiệu lực hiện hành – được coi là hợp đồng có điều kiện phát sinh. Ví dụ : K thỏa thuận hợp tác với Z rằng K sẽ mua con ngựa với giá 100.000.000 đồng của Z nếu con ngựa đó thắng trong cuộc đua ngày hôm sau. Ở đây, hợp đồng mua và bán ngựa đã giao kết nhưng chưa phát sinh hiệu lực hiện hành. Sự kiện được xem là “ điều kiện ” để hợp đồng phát sinh hiệu lực thực thi hiện hành là “ con ngựa sẽ thắng trong cuộc đua ngày mai ”. Theo đó “ thắng trong cuộc đua ngựa ngày mai ” được xem là điều kiện phát sinh của hợp đồng mua và bán ngựa. Các bên phải triển khai hợp đồng như đã thỏa thuận hợp tác. Pháp luật La Mã được xem là điều kiện phát sinh gắn liền với thời gian phát sinh hiệu lực thực thi hiện hành của hợp đồng. Hiệu lực phát sinh từ hợp đồng có điều kiện nhờ vào vào trường hợp ( sự kiện, điều kiện ) đã thỏa thuận hợp tác. Trong khoa học pháp lý cũng có quan điểm tựa như “ những sự kiện mà những bên tham gia thanh toán giao dịch dân sự thỏa thuận hợp tác làm điều kiện để xác lập thanh toán giao dịch hoặc hủy bỏ thanh toán giao dịch được hiểu là những hiện tượng kỳ lạ, sự vật, sự viẹc phát sinh trong đời sống xã hội thì khi sự kiện đó xảy ra là điều kiện để xác lập hoặc chấm hết thanh toán giao dịch dân sự ”. Ví dụ : Một người có con gái Là K, 18 tuổi, sẵn sàng chuẩn bị vào học Đại học. Ông ký hợp đồng với shop bán xe máy mua chiếc xe hiệu Yamaha với điều kiện khi con ông thi lấy được giấy phép lái xe thì ông sẽ mua cho con mình chiếc xe đó. Như vậy hợp đồng mua chiếc xe chỉ có hiệu lực hiện hành khi con gái là K được cấp giấy phép lái xe. Điều kiện cần là một trong những yếu tố để đạt được mục tiêu nào đó. Điều kiện đủ thì quy tụ nhiều yếu tố, chỉ cần có nó thì có được toàn bộ. Hãy nghĩ tới hai khái niệm “ động vật hoang dã có vú ” và “ mèo ”. Khái niệm “ động vật hoang dã có vú ” mang ý nghĩa tổng quát hơn khái niệm “ mèo ” khi “ động vật hoang dã có vú ” hoàn toàn có thể gồm có mèo, chó, dê, cừu, hổ, báo … còn “ mèo ” thì chỉ là mèo. Vì vậy, động vật hoang dã có vú là điều kiện cần để trở thành mèo. Bởi nếu chỉ có duy nhất động vật hoang dã có vú tất cả chúng ta sẽ dễ nhầm lẫn con vật tất cả chúng ta đang cần nghiên cứu và phân tích sang những loại khác như : Dê, cừu, hổ, báo … Bên cạnh đó, một con vật muốn được nhìn nhận là mèo thì nó phải chiếm hữu nhiều đặc tính của loài mèo như : Thuộc họ mèo, chân có móng vuốt, kêu meo meo … Tuy nhiên, mèo lại là điều kiện đủ để trở thành động vật hoang dã có vú. Bởi khi một con vật được cho là mèo thì nó nghiễm nhiên là động vật hoang dã có vú mà không cần xét thêm bất kỳ điều kiện nào khác. Như vậy, với bất kể mèo nào ta cũng đề có động vật hoang dã có vú nhưng không phải với bất kể “ động vật hoang dã có vú nào ” ta cũng có mèo.

2. Điều kiện cần và đủ tiếng anh là gì? 

Điều kiện cần và đủ tiếng anh là ” Necessary and sufficient conditions”

3. Mệnh đề điều kiện cần, điều kiện đủ:

Xét mệnh đề : “ Hai tam giác bằng nhau thì diện tích quy hoạnh của chúng bằng nhau ” Phát biểu điều kiện cần, điều kiện đủ, điều kiện cần và đủ : – Điều kiện cần : Hai tam giác có diện tích quy hoạnh bằng nhau là điều kiện cần để hai tam giác bằng nhau. – Điều kiện đủ : Hai tam giác bằng nhau là điều kiện đủ để hai tam giác đó có diện tích quy hoạnh bằng nhau. – Điều kiện cần và đủ là gì ? Là không có. Vì A đến B : đúng nhưng B đến A sai, vì “ hai tam giác có diện tích quy hoạnh bằng nhau nhưng chưa chắc đã bằng nhau ”. Nói “ con chó có bốn chân ” là đúng ( trong toán học gọi câu nói đó là Mệnh đề thuận ). Như vậy, con chó dứt khoát phải có bốn chân, con nào có hai chân, 3 chân, 5, 10, 15 chân ( Tóm lại số chân không phải là số 4 ) thì chắc như đinh không phải là con chó. Do đó, điều kiện cần để một con vật được là con chó thì phải có bốn chân.

Tuy nhiên, bây giờ có một con có bốn chân rồi thì đó có phải là con chó không (mệnh đề nghịch được phát biểu là: Con có bốn chân là con chó). Câu trả lời là chưa chắc vì mới chỉ có bốn chân thôi chưa đủ. Muốn là con chó phải thỏa mãn thêm điều kiện: Có đuôi, biết cắn người, ăn được… mới là cho. Đó chính là các điều kiện đủ.

Hơn nữa, khi nào người ta nói “ điều kiện cần và đủ ” tức là cả mệnh đề thuận và mệnh đề nghịch đều đúng. Ví dụ : Điều kiện cần và đủ để 1 số ít chia hết cho ba là tổng những chữ số phải chia hết cho ba. Như thế. Nếu số x chia hết cho ba thì tổng những chữ số của nó sẽ chia hết cho ba, đồng thời ngược lại, nếu tổng những chữ số của số Y chia hết cho ba thì chắc như đinh số Y sẽ chia hết cho ba. Trong Toán học, tất cả chúng ta rất hay gặp những mệnh đề có dạng “ Nếu P. thì Q. ” hoặc viết dưới dạng kí hiệu là P \ Rightarrow Q, ví dụ điển hình : + Nếu trời mưa thì nghỉ học. + Một số tự nhiên tận cùng bằng 5 thì chia hết cho 5. Trong những mệnh đề có dạng P \ Rightarrow Q này thì P. được gọi là giả thiết, Q. được gọi là Tóm lại. Hoặc, hoàn toàn có thể nói : + P. là điều kiện đủ để có Q. ; + Q. là điều kiện cần để co P.. Chúng ta xét mệnh đề “ Nếu trời mưa thì nghỉ học “. Rõ ràng, chỉ cần gặp trời mưa là đủ để suy ra nghỉ học, tức là trời mưa đủ để có nghỉ học, nên nó được gọi là điều kiện đủ. Ngược lại, nghỉ học thì chưa đủ để suy ra trời mưa, vì hoàn toàn có thể hôm đó cô giáo ốm. Nhưng tại sao lại gọi là điều kiện cần, vì không có nghỉ học ( tức là vẫn đi học ) thì chắc như đinh không hề có trời mưa. Lí do, nếu trời mưa thì đã nghỉ học rồi, đâu có đến lớp nữa. Như vậy, “ trời mưa là điều kiện đủ của nghỉ học ” còn “ nghỉ học là điều kiện cần của trời mưa “. Để hiểu rõ hơn, tất cả chúng ta liên tục xét vài ví dụ nữa. + Một số tự nhiên tận cùng bằng 5 thì chia hết cho 5. + Một số mà chữ số sau cuối là 5 thì chắc như đinh chia hết cho 5, nên hoàn toàn có thể nói đây Một số tự nhiên tận cùng bằng 5 là điều kiện đủ để số đó chia hết cho 5. Ngược lại, một số ít chia hết cho 5 là thiết yếu nhưng chưa đủ để suy ra số đó tận cùng bằng 5, vì số đó hoàn toàn có thể tận cùng là 0. Một số chia hết cho 6 thì chia hết cho 3. Tương tự, 1 số ít chia hết cho 6 thì chắc như đinh chia hết cho 3 nên một số ít chia hết cho 6 là điều kiện đủ để số đó chia hết cho 3. trái lại, một số ít chia hết cho 3 thì thiết yếu nhưng chưa đủ để suy ra số đó chia hết cho 6, nó còn phải chẵn nữa mới đủ. Trong đời sống, nói đến điều kiện cần điều kiện đủ tất cả chúng ta hoàn toàn có thể hiểu : + A là điều kiện cần của B nếu bất kể khi nào có B thì có A nhưng không phải khi nào có A cũng có B. + A là điều kiện đủ của B nếu bất kỳ khi nào ta có A thì có B nhưng không phải với bất kể B ta đều được A. Nếu mệnh đề P ⇒ Q và Q ⇒ P đều đúng thì ta có mệnh đề P ⇔ Q là một mệnh đề đúng. Khi đó, ta nói P. là điều kiện cần và đủ để có Q., hoặc cũng nói Q. là điều kiện cần và đủ để có P. Thuật ngữ “ cần và đủ ” còn được thay thế sửa chữa bằng những thuật ngữ “ khi và chỉ khi ”, “ nếu và chỉ nếu ” hoặc “ tương tự ”. Trong đời sống, tất cả chúng ta thường nói A là điều kiện cần và đủ của B nếu bất kỳ A nào ta cũng có B và bất kỳ B nào cũng có A.

Hay có thể xác định theo ví dụ như sau:

Xét mệnh đề : “ Phương trình bậc hai ax2 + bx + c = 0 có nghiệm thì Δ = b 2 – 4 ac ≥ 0 ″. Hãy phát biểu điều kiện cần, điều kiện đủ và điều kiện cần và đủ.

Hướng dẫn:

1 ) Điều kiện cần : Δ = b2 – 4 ac ≥ 0 là điều kiện cần để phương trình bậc hai ax2 + bx + c = 0 có nghiệm. 2 ) Điều kiện đủ : Phương trình bậc hai ax2 + bx + c = 0 có nghiệm là điều kiện đủ để Δ = b2 – 4 ac ≥ 0.

3) Điều kiện cần và đủ:

Phương trình bậc hai ax2 + bx + c = 0 có nghiệm là điều kiện cần và đủ để Δ = b 2 – 4 ac ≥ 0. Như vậy chắc rằng qua bài viết này tất cả chúng ta đã hoàn toàn có thể xác lập được mệnh đề cần và đủ trên trong thực tiễn. Với nội dung bài Phát biểu mệnh đề điều kiện cần và đủ trên đây chúng tôi xin trình làng tới những bạn học viên cùng quý thầy cô nội dung cần nắm vững giải pháp giải và điều kiện để mệnh đề đúng hay sai …. Dựa trên những kiến thức và kỹ năng nền tảng trong toán hoc.