Tìm hiểu về định nghĩa và những tính chất của tam giác cân

Có thể nói kiến thức và kỹ năng về tam giác cân và tam giác vuông cân là một trong những kiến thức và kỹ năng quan trọng trong chương trình toán hình ở trung học cơ sở. Cùng ôn lại định nghĩa và những đặc thù của nó qua bài viết này nhé .

Tam giác cân

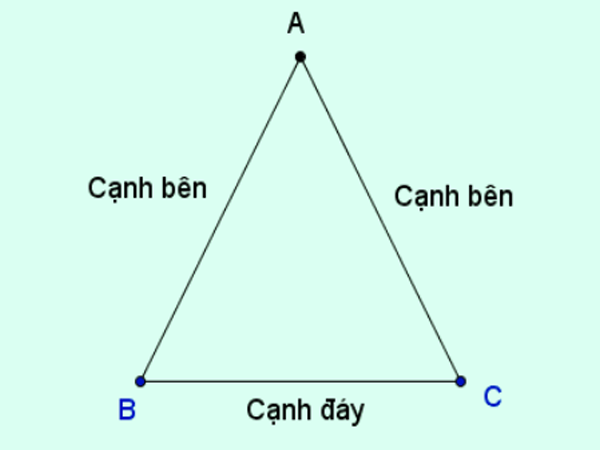
Tam giác cân ( Nguồn : Internet )

Định nghĩa

Tam giác cân là tam giác có 2 cạnh bên bằng nhau. Đỉnh của tam giác cân là giao điểm của hai cạnh bên. Góc được tạo bởi đỉnh được gọi là góc ở đỉnh, hai góc còn lại là góc đáy .

Tính chất

• Tính chất 1: Trong tam giác cân hai góc đáy bằng nhau

Ví dụ: Cho tam giác OAB cân tại O => góc OAB = góc OBA

• Tính chất 2: Tam giác có hai góc bằng nhau là tam giác cân.

Ví dụ: Cho tam giác BOD có góc BOD = góc BDO => tam giác BOD cân tại B

Tam giác vuông cân

Định nghĩa

Tam giác vuông cân vừa là tam giác vuông và vừa là tam giác cân. Trong tam giác vuông cân có hai cạnh góc vuông bằng nhau và mỗi góc nhọn bằng 45 độ .

Hình minh họa ( Nguồn : Internet )

Ví dụ: Cho tam giác ABC có cạnh AB vuông góc với AC và AB=AC

Suy ra : tam giác ABC vuông cân tại A .

Tính chất

• Tính chất 1: Tam giác vuông cân có 2 góc đáy bằng nhau và bằng 45 độ
• Tính chất 2: Các đường cao, đường trung tuyến và đường phân giác kẻ từ đỉnh có góc vuông của tam giác vuông cân trùng nhau và bằng một nửa cạnh huyền

Ví dụ: Cho tam giác ABC vuông cân tại A, D là trung điểm đoạn BC.

Suy ra AD vừa là đường cao, vừa là đường phân giác và đường trung tuyến của BC .
=> AD = BD = DC = ½ BC

Các dạng toán thường gặp

Bài tập 1: Cho tam giác ABC cân tại A, góc BAC bằng 40 độ, AH là đường cao. Điểm E, F lần lượt theo thứ tự thuộc các đoạn thẳng AH và AC sao cho góc EBA = góc FBC = 30 độ. Yêu cầu chứng minh AE = AF.

Bài giải :
Trên nửa mặt phẳng bờ AB ( chứa điểm C ) lấy điểm K sao cho tam giác ABK đều .
Xét tam giác cân ABC ta có :
ABC ^ = ACB ^ = 180 o – 40 o2 = 70 o ⇒ ABF ^ = ABC ^ – FBC ^ = 70 o – 30 o = 40 oVậy ABF ^ = BAF ^ ⇒ ∆ ABF cân tại F ⇒ FA = FB
Dựng điểm K sao cho KA = KB. Vậy KF là đường trung trực của AB
=> KF là đường phân giác của AKB ^ vì ∆ ABK đều
⇒ FKB ^ = 30 o ⇒ FKB ^ = EBA ^ 1 Theo giả thiết ∆ ABC cân tại A, có BAC ^ = 40 o, AH là đường caoSuy ra BAE ^ = 40 o2 = 20 oMặt khác : KAF ^ = KAB ^ – FAB ^ = 60 o – 40 o = 20 oVậy KAF ^ = BAE ^ 2
Chú ý : tam giác ABK đều nên AB = AK ( 3 )
Từ ( 1 ), ( 2 ) và ( 3 ) suy ra : ∆ KAF = ∆ BAE ⇒ AF = AE đpcm

Bài tập 2: Cho tam giác OBC cân tại O, kẻ OH vuông góc với BC (H thuộc BC). Yêu cầu:

1. Chứng minh HB = HC
2. OH là tia phân giác của góc BOC

Hình minh họa ( Nguồn : CIE Team )
Bài giải :

1. Xét 2 tam giác OBH và OCH, ta có:

OH chung ,
B ^ = C ^ và OB = OC ( vì tam giác OBC cân )
=> 2 tam giác OBH và OCH bằng nhau theo trường hợp cạnh góc cạnh
=> HB = HC ( hai cặp cạnh tương ứng )

2. Ta có: ∆OBH=∆OCH

=> BOH ^ = COH ^ ( hai góc tương ứng ) .

Bài tập 3: Trong các tam giác ở hình bên dưới (hình 116, hình 117, hình 118). Tam giác nào là tam giác cân và tam giác nào là tam giác đều? Giải thích?

Hình minh họa ( Nguồn : Internet )
Bài giải :
Xét hình 116 :
Ta có tam giác ABD cân vì AB = AD
=> BC = DE nên AB + BC = AD + DE hay AC = AE
Suy ra : tam giác ACE cân tại A
Xét hình 117 :
Ta có : G ^ = 180 oH ^ + I ^ = 180 o – 70 o + 40 o = 70 o
Suy ra tam giác GIH cân tại I
Xét hình 118 :
Tam giác OMN đều vì có 3 cạnh bằng nhau ( OM = MN = MO )
Tam giác OKM cân tại M vì có MO = MK
Tam giác PNO cân tại N vì có NO = NP

Ta có: OKM^+KOM^=OMN^=60omà OKM^=KOM^ nên OKM^=30oTương tự: OPM^=30oSuy ra: ∆KOP cân tại O vì có K^=P^=30o

Bên trên là những kiến thức và kỹ năng tổng quát về tam giác cân và tam giác vuông cân. Hy vọng bài viết hoàn toàn có thể giúp ích cho những bạn trong quy trình học tập và ôn luyện kỹ năng và kiến thức .
Cách tính diện tích hình chữ nhật như thế nào? : Công thức tính diện tích hình chữ nhật sẽ giúp học sinh có thể giải nhiều dạng bài toán. Đồng thời cũng có thể áp dụng để tính diện tích của một số vật dụng.Công thức tính diện tích quy hoạnh hình chữ nhật sẽ giúp học viên hoàn toàn có thể giải nhiều dạng bài toán. Đồng thời cũng hoàn toàn có thể vận dụng để tính diện tích quy hoạnh của 1 số ít đồ vật .Hình tròn và cách tính chu vi hình tròn : Bạn đang tìm hiểu về cách tính chu vi hình tròn, bài viết này sẽ hướng dẫn chi tiết cho bạn về cách tính chu vi hình tròn.Bạn đang tìm hiểu và khám phá về cách tính chu vi hình tròn trụ, bài viết này sẽ hướng dẫn chi tiết cụ thể cho bạn về cách tính chu vi hình tròn trụ .