5/5 – ( 2 bầu chọn )
Độ lệch chuẩn là gì? Độ lệch chuẩn (tiếng Anh: Standard Deviation hay Std Deviation – Ký hiệu độ lệch chuẩn: SD) là một công cụ thống kê thước đo đo lường mức độ phân tán của một tập hợp các giá trị so với giá trị trung bình của chúng.
Độ lệch chuẩn của một biến ngẫu nhiên, mẫu, tổng thể thống kê, tập dữ liệu hoặc phân phối xác suất là căn bậc hai của phương sai. Nó đơn giản hơn về mặt đại số, mặc dù trên thực tế ít mạnh mẽ hơn so với độ lệch tuyệt đối trung bình. Một đặc tính hữu ích của độ lệch chuẩn là, không giống như phương sai, nó được biểu thị bằng cùng một đơn vị với dữ liệu.
Độ lệch chuẩn thường hay được sử dụng trong những chiêu thức nghiên cứu và phân tích thống kê miêu tả trong luận văn
Bài viết này Mosl sẽ tổng hợp và giới thiệu toàn bộ tất cả các thông tin liên quan đến độ lệch chuẩn cho các bạn hình dung được khái niệm này 1 cách tổng quan và đẩy đủ nhất nhé!
Nội dung chính
1. Độ lệch chuẩn là gì ? Khái niệm tổng quát
1.1. Khái niệm
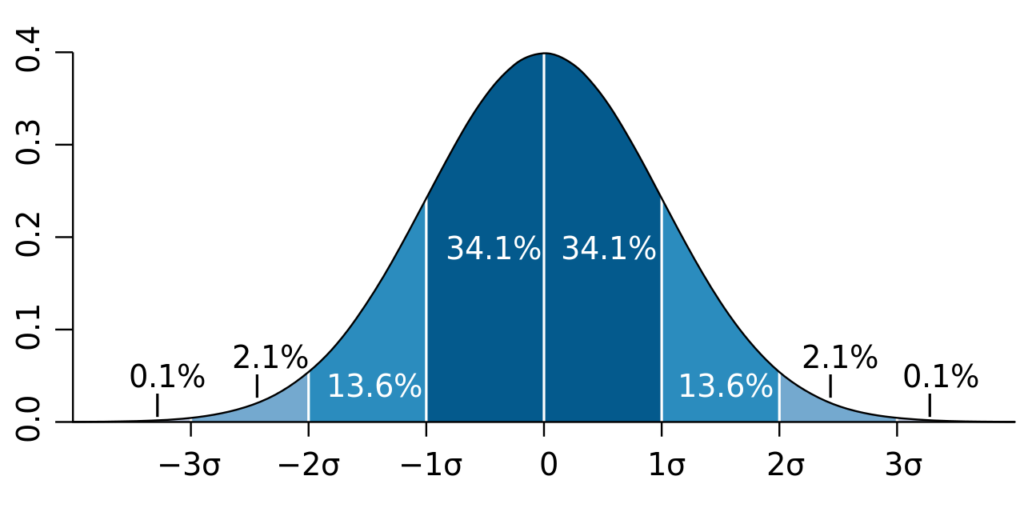
Độ lệch chuẩn – Standard Deviation (Std Deviation) được viết tắt với ký hiệu là SD , và được biểu diễn phổ biến nhất trong các văn bản và phương trình toán học bằng chữ cái Hy Lạp viết thường sigma σ , cho độ lệch chuẩn tổng thể hoặc chữ cái Latinh s.
1.2. Ý nghĩa của “Độ Lệch Chuẩn”
Độ lệch chuẩn có 6 ý nghĩa chính gồm:
- Độ lệch chuẩn cho biết được độ phân tán của giá trị thống kê so với giá trị trung bình, ở từng thời điểm khác nhau. Nếu độ lệch chuẩn thấp thì tính biến động không đáng kể và ngược lại.
- Độ lệch chuẩn của một biến ngẫu nhiên tổng thể thống kê hoặc phân phối xác suất là căn bậc hai của phương sai.
- Độ lệch chuẩn tương đối không giống như phương sai là nó được biểu thị bằng cùng một đơn vị với dữ liệu.
- Độ lệch chuẩn của một tổng thể hoặc mẫu và sai số chuẩn của một thống kê (ví dụ: của trung bình mẫu) là khá khác nhau, nhưng có liên quan với nhau.
- Độ lệch chuẩn lớn chỉ ra rằng các điểm dữ liệu có thể lan ra xa giá trị trung bình và độ lệch chuẩn nhỏ chỉ ra rằng chúng được tập hợp chặt chẽ xung quanh giá trị trung bình.
- Sai số chuẩn ước tính độ lệch chuẩn của một ước tính, chính nó đo lường mức độ ước tính phụ thuộc vào mẫu cụ thể được lấy từ tổng thể.
Funfact: Trong khoa học, người ta thường báo cáo cả độ lệch chuẩn của dữ liệu (như một thống kê tóm tắt) và sai số chuẩn của ước tính (như một thước đo cho sai số tiềm ẩn trong các phát hiện). Theo quy ước, chỉ những ảnh hưởng nhiều hơn hai sai số tiêu chuẩn từ một kỳ vọng rỗng mới được coi là “có ý nghĩa thống kê” , một biện pháp bảo vệ chống lại kết luận giả thực sự là do lỗi lấy mẫu ngẫu nhiên.
Tìm hiểu ngay: Mô hình sai số chuẩn hay sai số chuẩn là gì?
2. Công thức tính “ Độ Lệch Chuẩn ”
Độ lệch chuẩn của tổng thể là căn bậc 2 của phương sai tổng thể:
Tham khảo bài viết này để biết công thức tính phương sai tổng thể nhé!
Độ lệch chuẩn của mẫu:
Trong đó:
xi là giá trị của điểm i trong tập dữ liệu
x̄ là giá trị của tập dữ liệu
n là tổng số quan sát trong tập dữ liệu
N được tính trong tổng xích ma của xi
Giá trị x trung bình được tính bằng công thức trung bình tổng những quan sát .
Phương sai cho mỗi điểm dữ liệu được tính bằng cách trừ giá trị của quan sát với giá trị trung bình. Kết quả sau đó được bình phương và được chia cho số quan sát trừ một.
Xem thêm: Cách chứng minh đường trung trực lớp 7
Xem thêm: Phương sai (Variance) là gì? ngay nhé!
2.1. Ví dụ về “Độ Lệch Chuẩn”
Độ lệch chuẩn sỉ số của lớp tám bạn học sinh
Giả sử rằng hàng loạt sỉ số lớp chăm sóc là tám học viên trong một lớp học đơn cử. . Điểm của một lớp gồm tám học viên ( tức là một sỉ số thống kê ) là tám giá trị sau :
Phương sai là giá trị trung bình của các giá trị này:
Và sỉ số độ lệch chuẩn bằng căn bậc hai của phương sai:
2.2. Tính độ lệch chuẩn trong Excel
Tính độ lệch chuẩn rsd trong Excel, bạn sử dụng hàm STDEV với cú pháp:
STDEV(number1,[number2],…)
Trong đó:
- [Number1]: Đối số dạng số đầu tiên tương ứng với mẫu tổng thể (Bắt buộc).
- [Number2], … : Đối số dạng số từ 2 đến 255 tương ứng với mẫu tổng thể. (Tuỳ chọn)
Ví dụ: Tính độ lệch chuẩn trong excel với tập hợp M = {1; 1; 1; 2; 2; 0; 1; 9}
2.3. Hạn chế của độ lệch chuẩn
Độ lệch chuẩn cũng như bao khái niệm khác đều có những hạn chế nhất định như :
- Hạn chế lớn nhất của việc sử dụng độ lệch chuẩn là nó có thể bị ảnh hưởng bởi các điểm ngoại lai và các giá trị âm.
- Độ lệch chuẩn có giả định là phân phối chuẩn và xem tất cả sự không chắc chắn là rủi ro, ngay cả khi nó có lợi cho nhà đầu tư, ví dụ như khi lợi nhuận đạt mức trên trung bình.
- Độ lệch chuẩn bao nhiêu là cao, hạn chế của độ lệch chuẩn là thể hiện mức độ phân tán của dữ liệu tuy nhiên nó không thể dùng để đánh giá chính xác vấn đề trên mà phải dựa vào giá trị trung bình.
3. Quan hệ giữa Độ lệch chuẩn, Giá trị trung bình, Phương sai
3.1. Mối quan hệ giữa “Độ lệch chuẩn” và “Giá trị trung bình”
Giá trị trung bình (mean trong thống kê) và Độ lệch chuẩn của một tập hợp dữ liệu là thống kê mô tả thường được báo cáo cùng nhau trong các bài nghiên cứu.
Theo một nghĩa nào đó, độ lệch chuẩn là một thước đo “tự nhiên” của độ phân tán thống kê nếu trọng tâm của dữ liệu được đo về giá trị trung bình. Điều này là do độ lệch chuẩn so với giá trị trung bình nhỏ hơn bất kỳ điểm nào khác.
Câu lệnh chính xác như sau:
Giả sử x 1, …, x n là những số thực và xác lập hàm :
Sử dụng phép tính hoặc bằng cách hoàn thành bình phương , có thể chỉ ra rằng σ (r) có giá trị cực tiểu duy nhất tại giá trị trung bình:
Độ biến thiên cũng có thể được đo bằng hệ số biến thiên, hệ số này là tỷ số giữa độ lệch chuẩn và giá trị trung bình. Nó là một số không có thứ nguyên.
Lưu ý: Hệ số biến thiên có thể dùng để phân tích thống kê mô tả, theo đó khi hệ số này càng nhỏ thì mức độ phân tán hay dàn trải của biến dữ liệu đang xét càng thấp và ngược lại.
3.2. Mối quan hệ giữa “Độ lệch chuẩn” và “Phương sai”
Phương sai được tính bằng cách lấy giá trị trung bình của các quan sát trừ đi giá trị trung bình, sau đó bình phương từng kết quả và cuối cùng lấy giá trị trung bình của các kết quả này. Thế nên mối quan hệ giữa phương sai và độ lệch chuẩn như sau:
- Phương sai giúp xác định độ dàn trải của quan sát khi so sánh với giá trị trung bình.
- Phương sai lớn cho thấy có nhiều sự biến động trong các giá trị của tập dữ liệu và có thể có khoảng cách lớn hơn giữa giá trị các quan sát với nhau.
- Phương sai sẽ nhỏ hơn nếu tất cả các quan sát đứng gần nhau. Tuy nhiên, khái niệm này khó hiểu hơn nhiều so với độ lệch chuẩn, do phương sai biểu thị một kết quả bình phương.
- Phương sai do bình phương lên khiến nhiều điểm dữ liệu nằm ngoài độ lệch chuẩn, hay còn gọi là các điểm ngoại lai. Phương sai nhỏ hơn dẫn đến nhiều dữ liệu gần với giá trị trung bình.
4. Ứng dụng độ lệch chuẩn trong thực tiễn
4.1. Độ lệch chuẩn ứng dụng trong Tài chính
- Độ lệch chuẩn là một công cụ đặc biệt hữu ích trong xây dựng chiến lược đầu tư hay trong giao dịch vì nó đo lường mức độ biến động của thị trường và chứng khoán, cuối cùng dự đoán hiệu quả đàu tư.
Ví dụ : Nhà góp vốn đầu tư cần xem xét rằng những quỹ tăng trưởng tích cực thường có độ lệch chuẩn cao hơn so với những chỉ số sàn chứng khoán, vì những nhà quản trị hạng mục góp vốn đầu tư của họ đặt cược mức rủi ro đáng tiếc lớn hơn để đạt được doanh thu cao hơn mức trung bình .
- Độ lệch chuẩn thấp hơn không nhất thiết là tốt hơn mà tất cả phụ thuộc vào khoản đầu tư mà nhà đầu tư đang có và việc họ có sẵn sàng chấp nhận rủi ro hay không. Khi có sự biến động trong danh mục đầu tư, các nhà đầu tư nên xem xét khả năng chịu đựng của cá nhân họ đối với sự biến động này và mục tiêu đầu tư tổng thể của họ.
- Các nhà đầu tư ưa thích rủi ro có thể thoải mái với những chiến lược đầu tư vào các tài sản có độ biến động cao hơn mức trung bình, trong khi các nhà đầu tư bảo thủ (hay e ngại rủi ro) thì không.
- Standard Deviation của một mã cổ phiếu càng lớn hay phương sai giữa giá cổ phiếu và giá trị trung bình càng lớn thì cho thấy phạm vi giá của cổ phiếu đó càng lớn.
Ví dụ : Độ lệch chuẩn của CP Blue-chip không thay đổi thường thấp so với CP không ổn định .
- Độ lệch chuẩn được sử dụng trong thống kê và tài chính được áp dụng cho tỉ lệ hoàn vốn hàng năm của một khoản đầu tư. Độ lệch chuẩn làm sáng tỏ những sự biến động trong lịch sử khoản đầu tư.
- Đối với các nhà đầu tư mạo hiểm thường thích đầu tư vào các loại tài sản có biên độ biến động giá trị cao hơn mức trung bình. Còn các nhà đầu tư dài hạn thì sẽ e ngại rủi ro hơn rất nhiều.
- Độ lệch chuẩn là phương pháp đo lường rủi ro cơ bản được sử dụng rộng rãi trong giới đầu tư từ nhà phân, quản lý và cố vấn đầu tư thường hay sử dụng. Độ chênh lệch lớn cho thấy biên độ lợi nhuận của một quỹ đang chênh lệch so với lợi nhuận dự kiến. Độ lệch chuẩn khá dễ hiểu nên, nên công cụ thống kê này thường xuyên được sử dụng để báo cáo cho nhà đầu tư và khách hàng.
4.2. Độ lệch chuẩn ứng dụng trong Thời tiết
Ví dụ đơn giản: Hãy xem xét nhiệt độ tối đa trung bình hàng ngày cho hai thành phố, một trong đất liền và một trên bờ biển. Sẽ rất hữu ích khi hiểu rằng phạm vi nhiệt độ tối đa hàng ngày của các thành phố gần bờ biển nhỏ hơn so với các thành phố trong đất liền.
Do đó, trong khi hai thành phố này hoàn toàn có thể có cùng nhiệt độ tối đa trung bình, độ lệch chuẩn của nhiệt độ tối đa hàng ngày so với thành phố ven biển sẽ nhỏ hơn độ lệch chuẩn của nhiệt độ tối đa hàng ngày so với thành phố trong nước vì vào bất kể ngày đơn cử nào, nhiệt độ tối đa thực tiễn có nhiều năng lực hơn xa nhiệt độ tối đa trung bình của thành phố trong đất liền hơn là của thành phố ven biển .
4.3. Ứng dụng trong thử nghiệm công nghiệp và giả thuyết
- Độ lệch chuẩn thường được sử dụng để so sánh dữ liệu trong thế giới thực với một mô hình để kiểm tra mô hình.
Ví dụ, trong các ứng dụng công nghiệp, trọng lượng của sản phẩm ra khỏi dây chuyền sản xuất có thể cần phải tuân theo một giá trị pháp lý bắt buộc. Bằng cách sử dụng độ lệch chuẩn, giá trị tối thiểu và tối đa có thể được tính toán rằng trọng lượng trung bình sẽ nằm trong một số phần trăm rất cao của thời gian (99,9% trở lên). Nếu nó nằm ngoài phạm vi thì quy trình sản xuất có thể cần được sửa chữa.
- Trong khoa học thực nghiệm, một mô hình lý thuyết về thực tế được sử dụng. Vật lý hạt thông thường sử dụng tiêu chuẩn ” 5 sigma ” để tuyên bố một khám phá. Mức năm sigma có nghĩa là một trong 3,5 triệu cơ hội mà một biến động ngẫu nhiên sẽ mang lại kết quả. Mức độ chắc chắn này được yêu cầu để khẳng định rằng một hạt phù hợp với hạt boson Higgs đã được phát hiện trong hai thí nghiệm độc lập tại CERN , cũng dẫn đến tuyên bố về quan sát đầu tiên về sóng hấp dẫn , và xác nhận sự nóng lên toàn cầu .
5. Tổng kết
Tổng hợp lại những mục MOSL đã phân phối đến fan hâm mộ gồm :
- Khái niệm Độ lệch chuẩn là gì
- Ý nghĩa dđộ lệch chuẩn
- Công thức tính độ lệch chuẩn
- Mối quan hệ độ lệch chuẩn với phương sai và giá trị trung bình
- Ứng dụng của dđộ lệch chuẩn
- Phuong sai la gì? – Do lech chuan
Đến đây, MOSL xin chúc những bạn học tập và thao tác hiệu suất cao !
Xem thêm: Dịch vụ xử lý số liệu và hỗ trợ chạy Stata của Mosl.vn
Source: http://139.180.218.5
Category: tản mạn

