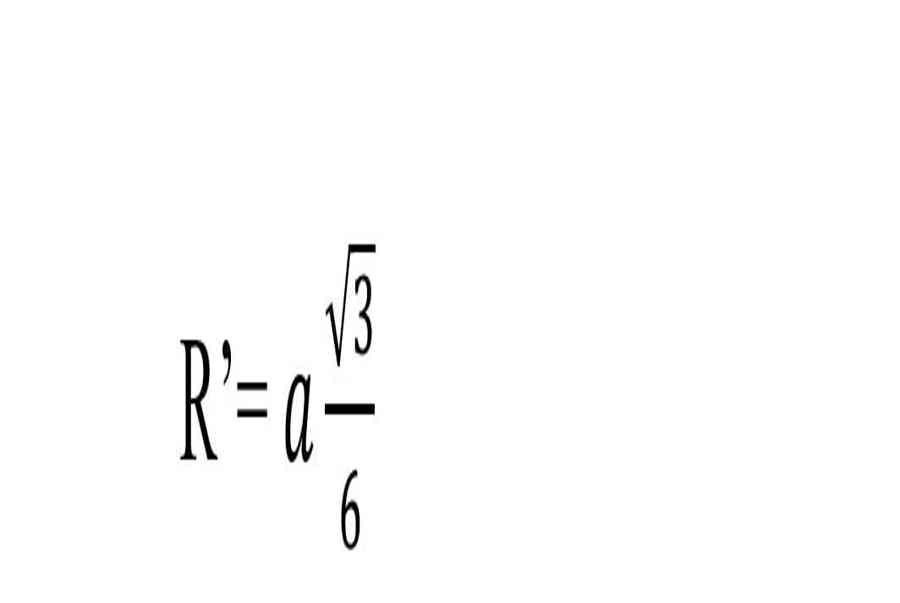đường cao của tam giác cân

I. ĐỊNH NGHĨA

Hình tam giác là hình hai chiều phẳng có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối những đỉnh với nhau .

II. HÌNH TAM GIÁC THƯỜNG

Các góc bên trong của một tam giác được gọi là góc trong. Góc kề bù với góc đó bằng tổng 2 góc không kề bù với nó .Hình tam giác thường là một mô hình cơ bản trong hình học và cũng là đa giác có số cạnh tối thiểu ( 3 cạnh ) .

Công thức tính chu vi tam giác thường

Hình tam giác thường có chu vi bằng tổng độ dài 3 cạnh .

P = a + b + c

Trong đó : a, b, c lần lượt là 3 cạnh của tam giác thường .

Công thức tính diện tích tam giác thường

Diện tích tam giác thường hoàn toàn có thể tính bằng cách lấy chiều cao nhân với độ dài đáy, sau đó tổng thể chia cho 2. Nói cách khác, diện tích quy hoạnh tam giác thường sẽ được tính bằng 1/2 tích của chiều cao và chiều dài cạnh đáy của tam giác đó .

S = ½ bh

• Trong đó: S là diện tích tam giác thường.
• b là độ dài một cạnh bất kỳ trong tam giác.
• h là độ dài của chiều cao được hạ từ đỉnh đối diện xuống cạnh đó.

III. HÌNH TAM GIÁC CÂN

Tam giác cân là loại tam giác đặc biệt quan trọng có hai cạnh bằng nhau .

Tính chất của hình tam giác cân

• Trong tam giác cân thì có 2 cạnh bằng nhau và 2 góc ở đáy bằng nhau.
• Tam giác vuông cân là tam giác vuông có 2 cạnh hay 2 góc ở đáy bằng nhau.
• Đường cao được hạ từ đỉnh xuống đáy trong tam giác cân cũng chính là đường trung tuyến và đường phân giác của tam giác đó.

Công thức tính chu vi tam giác cân

Hình tam giác cân có các tích chất của tam giác thường, do đó chu vi của nó cũng tính theo cách tương tự:

P = a + b + c

Công thức tính diện tích tam giác cân

S = ½ x b x h

Với : b là độ dài đáy ứng với đường cao h

IV. TAM GIÁC VUÔNG

Hình tam giác vuông là tam giác có một góc vuông .

Công thức tính chu vi tam giác vuông

P = a + b + c

( a, b, c là độ dài 3 cạnh tam giác )

Công thức tính diện tích tam giác vuông

S = ½ x b x h

Chú ý : 2 cạnh góc vuông trong tam giác vuông cũng đóng vai trò là đường cao và đáy trong công thức tính trên

Công thức tính đường cao trong tam giác

Giả sử có một tam giác ABC vuông tại A

• Áp dụng định lý Pi-ta-go:

• ‍Áp dụng công thức lượng giác: AC = sinB x BC = cosC x BC‍
• Sử dụng hệ thức lượng

V. TAM GIÁC ĐỀU

Hình tam giác đều là tam giác có 3 cạnh bằng nhau, 3 đường cao bằng nhau, 3 đường trung tuyến bằng nhau và 3 đường phân giác bằng nhau

Công thức tính chu vi tam giác đều

Do hình tam giác đều có 3 cạnh như nhau nên chu vi tam giác được tình bằng 3 lần cạnh bất kỳ trong tam giác đó ( độ dài cạnh là a )

P = 3a

Công thức tính diện tích tam giác đều

Công thức tính Bán kính đường tròn ngoại tiếp

Công thức tính Bán kính đường tròn nội tiếp

Công thức tính Chiều cao của tam giác đều

Với kỹ năng và kiến thức tổng hợp không thiếu nhất về hình tam giác như trên, chúng tôi mong ước đem lại tác dụng tốt nhất cho những bạn .

Video liên quan