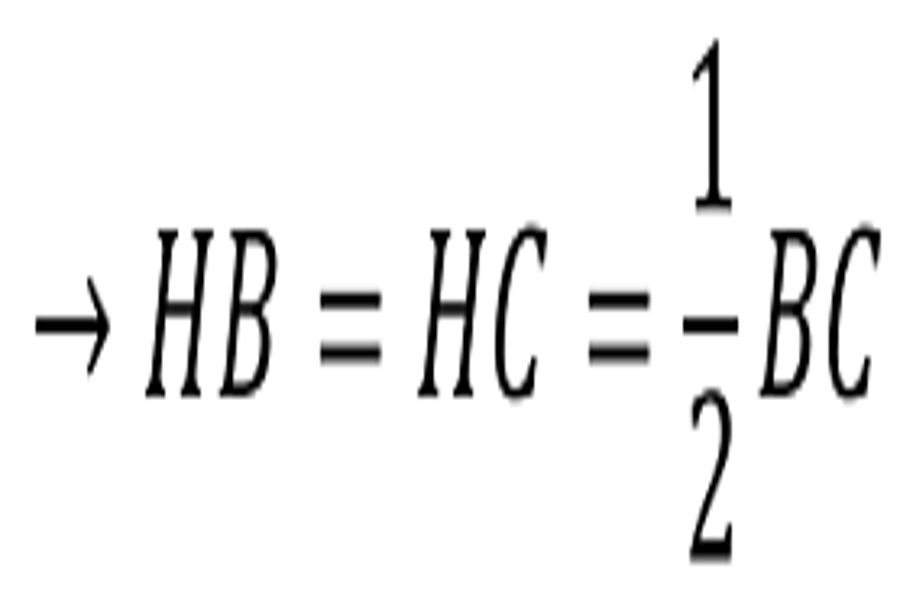Công thức Tính đường cao trong tam giác vuông cân ? – Đáp Án Chuẩn

Tam giác vuông cân là một tam giác đặc biệt và đường cao trong tam giác là một đường thẳng có tính chất rất là quan trọng là liên quan hầu hết tới các bài tập toán hình học. Vậy đường cao là gì và cách tính đường cao trong tam giác vuông cân sẽ được tính như thế nào thì các bạn hãy cùng Dapanchuan.com theo dõi bài viết dưới đây nhé.

Định nghĩa đường cao trong tam giác vuông cân và các loại tam giác khác

Đường cao trong tam giác là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện. Cạnh đối diện này được gọi là đáy ứng với đường cao. Độ dài của đường cao là khoảng cách giữa đỉnh và đáy.

Công thức tính đường cao trong tam giác

Đối với những bài toán về hình tam giác vuông cân và những loại tam giác khác, ngoài công thức tính diện tích quy hoạnh, tính chu vi thì cách tính đường cao trong tam giác vuông cân và những loại tam giác khác cũng là một trong những dạng bài toán hình học được đưa vào những bài kiểm tra .
Để giải được những bài toán về đường cao trong tam giác vuông cân và những loại tam giác khác, việc tiên phong mọi người cần phải nắm rõ được công thức tính đường cao của vuông và những loại tam giác khác. Mỗi loại tam giác lại có một công thức tính đường cao riêng không liên quan gì đến nhau, điều này khiến nhiều người gặp khó khăn vất vả khi giải bài tập toán. Để nắm rõ hơn về công thức tính đường cao vuông và những loại tam giác khác

Công thức Tính đường cao trong tam giác vuông cân:

Giả sử có tam giác vuông ABC vuông tại A như hình vẽ trên :

Công thức tính cạnh và đường cao trong tam giác vuông:

Trong đó:

a, b, c lần lượt là các cạnh của tam giác vuông như hình trên;

b’ là đường chiếu của cạnh b trên cạnh huyền;

c’ là đường chiếu của cạnh c trên cạnh huyền;

h là chiều cao của tam giác vuông được kẻ từ đỉnh góc vuông A xuống cạnh huyền BC.

Công thức tính cạnh huyền tam giác vuông cân

Theo định lý pitago, công thức tính cạnh huyền tam giác vuông cân đối căn bậc hai của bình phương hai cạnh còn lại

Trong đó:

c là cạnh huyền của tam giác vuông cân

a, b lần lượt là 2 cạnh còn lại
Như vậy những bạn hoàn toàn có thể dựa vào những công thức cạnh và đường cao trong tam giác vuông ở trên để xử lý những bài toán
Công thức tính đường cao trong tam giác thường

Công thức để tính đường cao trong tam giác là công thức Heron:

Trong đó:

a, b, c: Là độ dài các cạnh.

ha: Là khoảng cách độ dài từ đỉnh A tới cạnh đáy BC.

p: Là nửa chu vi.

Nửa chu vi được tính theo công thức:

Công thức tính đường cao trong tam giác đều

Giả sử tam giác đều ABC có độ dài cạnh bằng a như hình vẽ :

Trong đó:

h là đường cao của tam giác đều

a là độ dài cạnh của tam giác đều

Công thức tính đường cao trong tam giác cân

Tam giác cân là tam giác có 2 cạnh bằng nhau, số đo 2 góc đáy bằng nhau. Giả sử các bạn có tam giác ABC cân tại A, đường cao AH vuông góc tại H như hình bên:

Công thức tính đường cao AH:

Vì tam giác ABC cân tại A nên đường cao AH đồng thời là đường trung tuyến nên :

Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có :