Tính chất đường trung trực của tam giác, định nghĩa và bài tập – Thiết bị vệ sinh công nghiệp Palada

Đường trung trực là khái niệm được xuất hiện trong chương trình môn Toán lớp 7. Tuy nhiên thì tính chất đường trung trực vẫn được tiếp tục đưa vào bài tập dạng nâng cao của các lớp trên. Bài viết dưới đây sẽ tổng hợp các nội dung về tính chất đường trung trực của một đoạn thẳng và tính chất ba đường trung trực của tam giác, hãy cùng theo dõi nhé.

1. Khái niệm đường trung trực

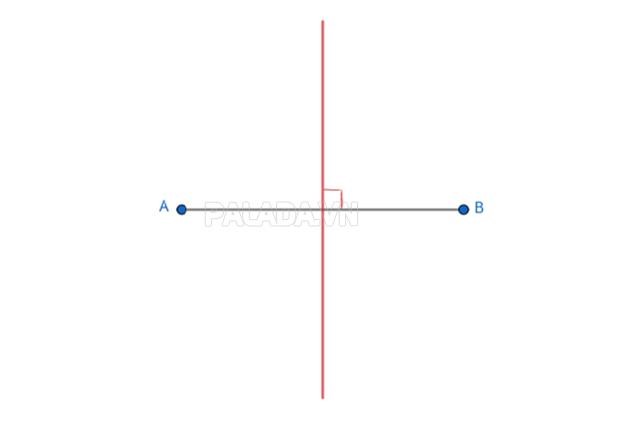
Đường trung trực một đoạn thẳng trong hình học phẳng là một đường thẳng vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó .

2. Tính chất đường trung trực 1 đoạn thẳng

Định lý 1 tính chất đường trung trực của đoạn thẳng

Điểm mà nằm trên đường trung trực của 1 đoạn thẳng thì nó cách đều 2 điểm mút của đoạn thẳng đó .

Định lý 2 tính chất đường trung trực của đoạn thẳng

Điểm nào cách đều 2 điểm mút của một đoạn thẳng thì nó nằm trên đường trung trực của đoạn thẳng đó.

3. Đường trung trực tam giác

Đường trung trực từng cạnh của tam giác được gọi là đường trung trực của tam giác đó .

4. Tính chất của ba đường trung trực một tam giác

Tính chất 3 đường trung trực của một tam giác thường

Trong tam giác, ba đường trung trực sẽ cùng đi qua ( gọi là đồng quy ) một điểm. Điểm này có đặc thù là cách đều ba đỉnh của tam giác và chính là tâm của đường tròn ngoại tiếp với tam giác đó .

Tính chất đường trung trực một tam giác vuông

Trong tam giác vuông ta có giao điểm của ba đường trung trực là trung điểm của cạnh huyền .

Tam giác cân

Trong tam giác cân thì đường trung trực tương ứng với cạnh đáy cũng đồng thời là đường trung tuyến, đường phân giác, đường cao cùng xuất phát từ đỉnh đối lập với cạnh đó .

5. 6 dạng bài tập về tính chất đường trung trực

Dạng 1: Chứng minh là đường trung trực của một đoạn thẳng

Cách giải : Ví dụ để chứng tỏ đường thẳng d chính là đường trung trực của đoạn thẳng AB cho trước, ta cần chứng tỏ d chứa cả hai điểm cách đều A và B hoặc sử dụng định nghĩa đường trung trực .

Dạng 2: Chứng minh 2 đoạn thẳng là bằng nhau

Cách giải : Ta hoàn toàn có thể giải dạng toán này bằng cách sử dụng định lý 1 đặc thù đường trung trực của một đoạn thẳng : Điểm nào nằm trên đường trung trực của một đoạn thẳng thì cách đều 2 mút của đoạn thẳng đó .

Dạng 3: Bài toán giá trị nhỏ nhất

Cách giải :
+ Bước 1 : Sử dụng đặc thù đường trung trực của một đoạn thẳng nhằm mục đích thay độ dài của đoạn thẳng thành độ dài của một đoạn thẳng khác bằng với nó .
+ Bước 2 : Sử dụng bất đẳng thức trong 1 tam giác để tìm giá trị nhỏ nhất .
Bất đẳng thức tam giác được phát biểu là trong một tam giác chiều dài của một cạnh phải nhỏ hơn tổng, nhưng lớn hơn hiệu hai cạnh còn lại .

Dạng 4: Xác định tâm của đường tròn ngoại tiếp tam giác

Cách giải : Sử dụng đặc thù giao điểm những đường trung trực của tam giác .
Ba đường trung trực một tam giác sẽ cùng đi qua một điểm. Điểm này luôn cách đều ba đỉnh của tam giác đã cho .

Dạng 5: Bài toán đường trung trực tam giác cân

Cách giải : Trong tam giác cân đường trung trực của cạnh đáy cũng đồng thời chính là đường trung tuyến và đường phân giác với cạnh đáy .

Dạng 6: Bài toán đường trung trực tam giác vuông

Cách giải : Trong tam giác vuông giao điểm những đường trung trực chính là trung điểm của cạnh huyền .

6. Chứng minh đường thẳng đường trung trực của đoạn thẳng

Để chứng tỏ đường trung trực của đoạn thẳng ta có 5 cách :
Cách 1 : Chúng ta hãy triển khai chứng tỏ rằng đường thẳng d là vuông góc với đoạn thẳng AB tại trung điểm .
Cách 2 : Chứng minh 2 điểm trên d là cách đều điểm A và B .

Cách 3: Sử dụng tính chất của đường trung tuyến, chiều cao.

Cách 4 : Sử dụng đặc thù đối xứng của trục .
Cách 5 : Sử dụng đặc thù đoạn nối tâm của 2 đường tròn cắt nhau tại 2 điểm .

7. Bài tập về tính chất đường trung trực có lời giải

Câu 1 : Cho tam giác ABC, hãy tìm ra một điểm O sao cho O cách đều ba điểm A, B, C đã cho đó .

Giải:

Câu 2 : Cho hai điểm D, E ở trên đường trung trực của đoạn thẳng BC. Hãy chứng tỏ rằng tam giác BDE bằng tam giác CDE .

Giải:

Câu 3 : Cho hình dưới đây, M là một điểm nằm tùy ý trên đường thẳng a. Vẽ điểm C sao cho có đường thẳng a là trung trực của AC. So sánh tổng MA + MB với BC .

Giải:

8. Hướng dẫn vẽ đường trung trực của đoạn thẳng

Cách 1 : Vẽ bằng compa
Bước 1 : Vẽ một đoạn thẳng AB .

Bước 2 : Quay 2 đường tròn có tâm chính là 2 đầu đoạn thẳng, có nửa đường kính bằng độ dài đoạn thẳng .

Bước 3 : Vẽ đường nối giao điểm 2 vòng tròn trên là C và D, đường nối đó chính là đường trung trực .

Cách 2 : Bằng thước và eke
Bước 1 : Vẽ đoạn thẳng AB .

Bước 2 : Sau đó xác lập trung điểm I của AB .

Bước 3 : Vẽ một đường thẳng d vuông góc với đoạn thẳng AB tại điểm I .

9. Một số câu hỏi về tính chất đường trung trực

– Số đường trung trực có trong một đoạn thẳng ?

Trả lời: Đường trung trực là đường thẳng chỉ đi qua duy nhất trung điểm của đoạn thẳng mà mỗi đoạn thẳng lại chỉ có một trung điểm. Vậy suy ra một đoạn thẳng chỉ có một đường trung trực.

– Cách viết phương trình của đường trung trực đoạn thẳng :
Trả lời : Để viết được phương trình đường trung trực của đoạn thẳng thì ta dựa vào định lý 1 : “ Điểm nào nằm trên đường trung trực của một đoạn thẳng thì nó sẽ cách đều hai mút của đoạn thẳng đó ”. Tức là nếu điểm M thuộc đường thẳng AB thì ta có MA = MB .
Trên đây là tổng hợp về đặc thù đường trung trực của một đoạn thẳng và đặc thù 3 đường trung trực của tam giác cùng những dạng bài tập phổ cập thường gặp để những em học viên tìm hiểu thêm. Chúc những em vận dụng thành công xuất sắc và đạt thành tích tốt trong học tập .