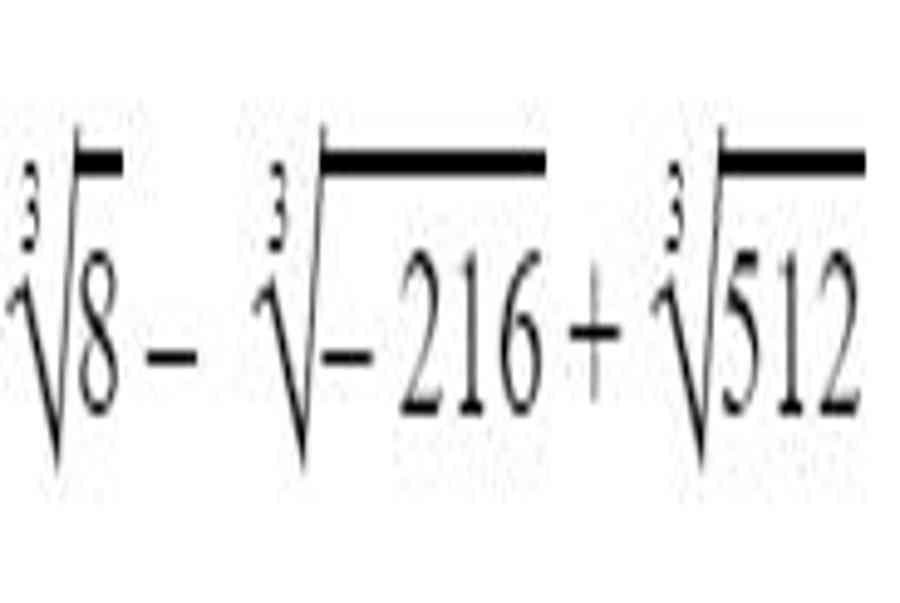Căn bậc 3 lớp 9 – Giải toán 9 nhanh nhất cùng Toppy

Căn bậc 3 là một trong những kiến thức không thực sự khó nắm bắt. Tuy nhiên, những dạng toán ứng dụng căn bậc 3 vào để giải quyết lại không hề đơn giản. Do đó, người dùng cần phải nắm chắc những kiến thức và tính chất quan trọng của căn bậc 3. Từ đó có thể vận dụng một cách hợp lý vào các bài toán. Tiếp tục cùng Toppy chinh phục căn bậc 3 lớp 9 ở ngay bài viết dưới đây. 

Căn bậc ba là gì?

Căn bậc ba của một số x bất kỳ là a nếu như: a3 = x. Căn bậc ba của x được ký hiệu một cách đơn giản là 3√x. Ký hiệu này giống với căn bậc 2 nhưng thêm số 3 ở phần đầu của căn. 

Những số có căn bậc 3 là những số thực. Đây là một trong những đặc thù khác với căn bậc 2 là căn bậc chẵn. căn bậc 2 nhu yếu những số thực không âm. căn bậc 3 thì không phải như vậy. Ví dụ : 3 √ – 8 = – 2

Những tính chất cơ bản của căn bậc 3 lớp 9

Chúng ta cần quan tới 3 tính chất cơ bản nhất của một căn bậc ba thông thường. Đó là:

• x
• 3 √x. y=3 √x.3 √y
• Trong trường hợp y khác 0 ta có :

Người ta sử dụng 3 đặc thù cơ bản trên đây để triển khai những bài toán có tương quan tới căn bậc 3. Trong đó, đặc thù 2 và 3 là những đặc thù được sử dụng nhiều hơn cả .

Các dạng bài tập chứa căn bậc 3 lớp 9 

Cùng điểm qua những dạng bài tập cơ bản có chứa căn bậc 3 hoặc cần sử dụng căn bậc 3 trong quy trình làm bài .

Dạng 1: Thực hiện phép tính

Thực hiện phép tính là dạng toán cơ bản nhất của những bài toán tương quan tới căn bậc hai căn bậc ba. Đối với dạng bài tập này thì đa phần sử dụng 2 công thức :
3 √ x3 = x và ( 3 √ x ) 3 = x
Bên cạnh đó, còn phối phối hợp sử dụng những hằng đẳng thức lập phương như : lập phương của một tổng, lập phương của một hiệu, tổng 2 lập phương, hiệu 2 lập phương .

Dạng 2: Chứng minh đẳng thức, bất đẳng thức

Đây cũng là một trong những dạng toán khá phổ biến có sử dụng giải toán 9 căn bậc ba. Không có phương pháp giải chung cho dạng toán này. Thông thường, có thể là tính toán trực tiếp, rút gọn,… Đối với các bài toán phức tạp thì thường là rút gọn về dạng đơn giản hơn để chứng minh. Sử dụng phối kết hợp 3 tính chất phía trên để làm bài. 

Dạng 3: So sánh hai căn bậc 3

So sánh hai căn bậc 3 là dạng toán cơ bản còn lại của những bài toán tương quan tới căn bậc 3. Đây không phải dạng toán khó nếu chỉ so sánh hai căn bậc 3 thường thì. Vẫn sử dụng giải pháp X Đối với các bài toán căn bậc ba lớp 9 nâng cao thì cần đưa về dạng đơn giản bằng cách phân tích nhân tử, hằng đẳng thức,… để có thể giải quyết 

Trắc nghiệm căn bậc 3 lớp 9 

Toppy có một số bài tập trắc nghiệm liên quan tới giải toán 9 căn bậc 3 muốn cung cấp cho bạn đọc. Đây là các bài tập tương đối đơn giản dành cho những người mới làm quen với dạng toán căn bậc ba lớp 9. 

Câu 1 : căn bậc 3 của 9 kí hiệu là gì ?

1. 3 √9
2. 9
3. 9 √3
4. 2 √9

Dựa vào khái niệm của căn bậc 3. căn bậc 3 của 9 sẽ được viết dưới dạng 3 √ 9 .
Chọn A.

Câu 2 : Kết quả của phép tính3 √27–3 √125là gì ?

1. 2
2. – 2
3. 3 √98
4. –3 √98

Ta có : 3 √ 27 – 3 √ 125 = 3 – 5 = – 2 .
Chọn B.

Câu 3 : Tìm giá trị của x đểcó nghĩa. Chọn câu đúng nhất .

1. x = 4

2. x = 5

   Xem thêm: Stt bầu trời – Những câu nói, cap hay về bầu trời

3. x = 8
4. x là số thực

Tất cả những số thực đều có căn bậc 3. Do đó để có nghĩa thì 16 x – 5 phải là số thực => x là số thực .
Chọn D.

Câu 4: Kết quả của phép tính  là gì?

1. 14
2. 16
3. 18
4. 12

Ta có : = 2 – ( – 6 ) + 8 = 16
Chọn B.

Câu 5 : Rút gọn biểu thức :

1. a + b
2. a – b
3. a. b
4. a / b

Sử dụng hằng đẳng thức hiệu 2 lập phương ta được : = ( 3 √ a ) 3 – ( 3 √ b ) 3 = a – b .
Chọn B.

Câu 6 : Giải phương trình ( 23 √x+ 5 ) (23 √x- 5 )= – 21

1. x = – 1
2. x = 3
3. x = – 1 hoặc x = 1
4. x = 3 hoặc x = – 3

Sử dụng hằng đẳng thức ta được : ( 23 √ x ) 2 – 25 = – 21 => 43 √ x2 = 4 => x2 = 1. Vậy x = 1 hoặc x = – 1 .
Chọn C.

Câu 7 : Đâu không phải là đặc thù của căn bậc ba .

1. x
2. 3 √x. y=3 √x.3 √y
3. 
4. x = y ⬄3 √x

Dựa vào các tính chất liệt kê ở phần đầu, dễ nhận thấy các tính chất của căn bậc ba bao gồm các đáp án A, B và C. 

Chọn D.

Trên đây là toàn bộ những kiến thức về căn bậc 3 lớp 9 dành cho bạn đọc tham khảo. Để có thể học tốt toán 9 thì căn bậc 3 chắc chắn là kiến thức không thể bỏ qua. Còn chần chờ gì nữa khi không đồng hành cùng Toppy đi chinh phục các dạng toán mới lạ nhất. 

 Xem thêm: