Hàm số nghịch biến khi nào? Lý thuyết và bài tập mẫu

Hàm số đồng nghịch biến là kiến thức và kỹ năng trọng điểm của chương trình toán đại trà phổ thông. Vậy Hàm số nghịch biến khi nào ? Định nghĩa và điều kiện kèm theo của hàm số nghịch biến là gì ? GiaiNgo sẽ giúp bạn giải đáp vướng mắc qua bài viết này .

Dạng toán hàm số nghịch biến thường xuất hiện nhiều trong các đề thi THPTQG và trong các đề thi thử của các trường trên toàn quốc. Nhiều bạn vẫn thắc mắc Hàm số nghịch biến khi nào? Điều kiện của nó là gì? Bài viết này của GiaiNgo sẽ giải đáp và giúp các bạn ôn tập tốt dạng toán này!

Định nghĩa hàm số nghịch biến

Hàm số nghịch biến, đồng biến hay còn gọi là hàm số đơn điệu .
Cho K là một khoảng chừng, một đoạn hoặc 50% khoảng chừng và y = f ( x ) là một hàm số xác lập trên K .
Hàm số y = f ( x ) được gọi là nghịch biến ( giảm ) trên K, nếu :

• ∀ x1, x2 ∊ K mà x1 f (x2)
• Biểu diễn đồ thị hàm số là một đường đi xuống.

Hàm số nghịch biến khi nào?

Hàm số f nghịch biến trên K khi và chỉ khi :

Điều kiện đủ để hàm số nghịch biến

Cho hàm số f có đạo hàm trên K .
Nếu f ‘ ( x ) Định lí mở rộng

Chỉ xét K là một khoảng chừng
Giả sử hàm số f có đạo hàm trên K
Nếu f ‘ ( x ) ≤ 0 với mọi x ∈ K và f ‘ ( x ) = 0 chỉ tại 1 số ít hữu hạn điểm thuộc K thì f nghịch biến trên K .

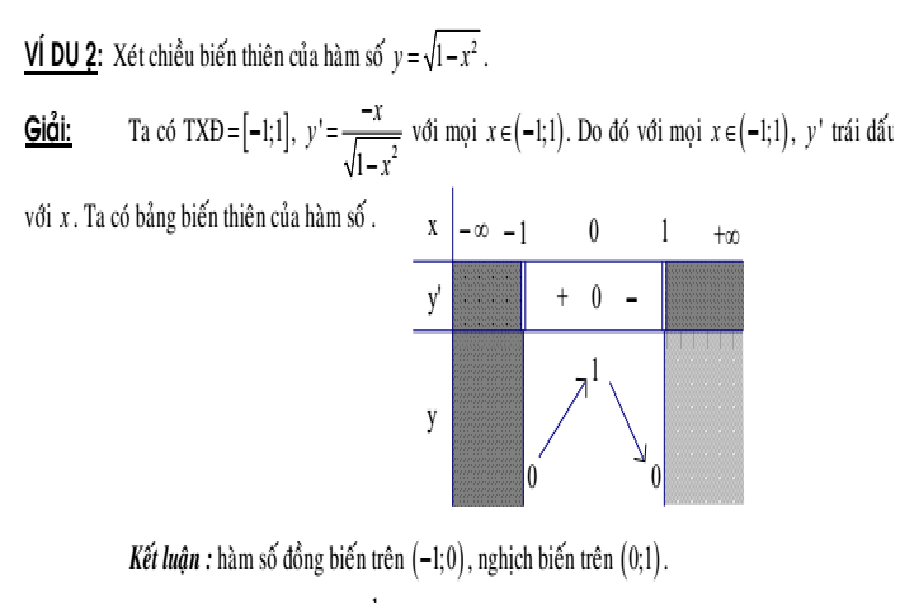
Phương pháp xét tính đơn điệu của hàm số

• Tìm tập xác định
• Tính đạo hàm f'(x). Tìm các điểm xi (i= 1, 2 ,…, n) mà tại đó f'(x) bằng 0 hoặc không xác định.
• Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
• Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Bài tập mẫu

Dạng toán xét sự đồng biến, nghịch biến của hàm số

Kết luận: Hàm số đồng biến trên các khoảng (-∞;2) và (4;+∞), nghịch biến trên khoảng (2;4).

Dạng toán tìm m để hàm số nghịch biến

Ví dụ 4: Tìm m để hàm số:  nghịch biến trong khoảng (-1/2;1/2)

Qua những kỹ năng và kiến thức trên mà GiaiNgo san sẻ, kỳ vọng bạn đọc sẽ nắm vững kỹ năng và kiến thức về hàm số nghịch biến khi nào và ôn tập thật tốt. Chúc những bạn thành công xuất sắc !