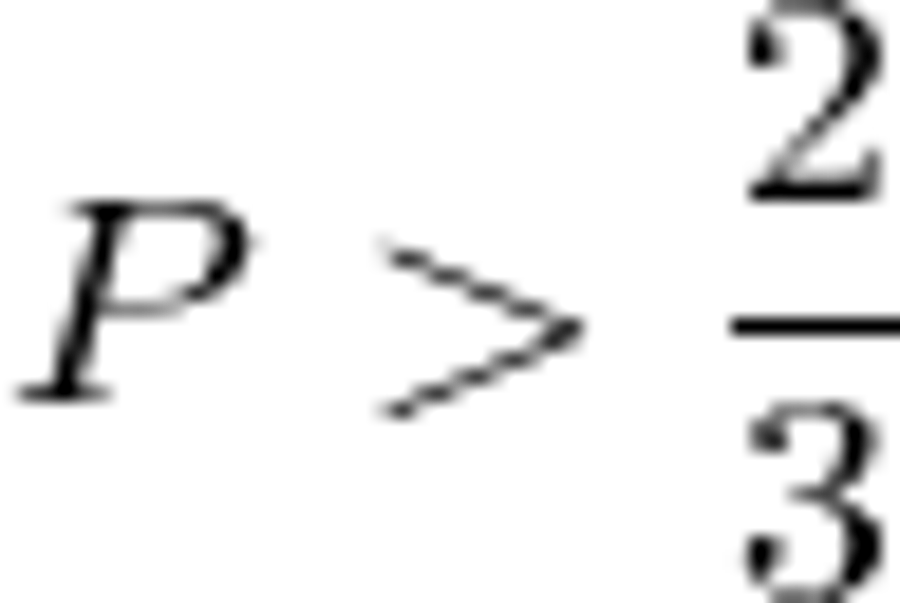Nội dung chính
Hướng dẫn cách rút gọn biểu thức chứa căn cho học sinh lớp 9. Đây là dạng toán chắc chắn có trong các đề thi tuyển sinh vào lớp 10 môn Toán.
Để giải được bài tập rút gọn và tính giá trị của biểu thức chứa căn bậc hai tất cả chúng ta cần ôn lại kim chỉ nan căn thức bậc hai. Tức là :
Biến đổi biểu thức chứa căn bậc hai
Vận dụng những quy tắc dưới đây :
1. Đưa thừa số ra ngoài dấu căn
Với hai biểu thức 


Bạn đang đọc: Cách rút gọn biểu thức chứa căn bậc hai – Toán 9
Nếu 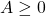
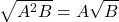
Nếu 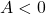
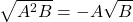
2. Đưa thừa số vào trong dấu căn
Với và thì 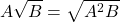
Với 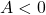
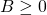
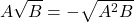
3. Khử mẫu của biểu thức lấy căn
Với hai biểu thức mà 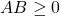
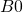
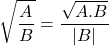
4. Trục căn thức ở mẫu
Với hai biểu thức A, B mà B > 0 ta có :
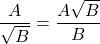
Với các biểu thức 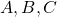
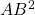
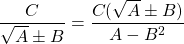
Với các biểu thức mà 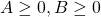
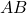
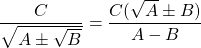
Bài tập: Thực hiện phép tính chứa căn bậc hai dưới đây:
1) 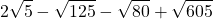
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
Cách rút gọn biểu thức chứa căn bậc hai
Phương pháp rút gọn:
– Phân tích đa thức tử và mẫu thành nhân tử ;– Tìm ĐKXĐ ( Nếu bài toán chưa cho ĐKXĐ )– Rút gọn từng phân thức ( nếu được )– Thực hiện những phép biến hóa như nhau như :+ Quy đồng ( so với phép cộng trừ ) ; nhân, chia .+ Bỏ ngoặc : bằng cách nhân đơn ; đa thức hoặc dùng hằng đẳng thức+ Thu gọn : cộng, trừ những hạng tử đồng dạng .+ Phân tích thành nhân tử – rút gọn
* Chú ý: Trong mỗi bài toán rút gọn thường có các câu thuộc các loại toán: Tính giá trị biểu thức; giải Phương trình; bất phương trình; tìm giá trị của biến để biểu thức có giá trị nguyên; tìm giá trị nhỏ nhất ,lớn nhất…Do vậy ta phải áp dụng các Phương pháp giải tương ứng, thích hợp cho từng loại bài.
Ví dụ: Cho biểu thức:
a/ Rút gọn
b/ Tìm giá trị của
Giải:
a / Rút gọn :
– Phân tích:
– ĐKXĐ:
– Rút gọn:
b / Tìm giá trị của để có giá trị nguyên :
– Chia tử cho mẫu ta được:
– Lý luận: nguyên
Vậy với
Bài tập rút gọn, tính giá trị biểu thức chứa căn lớp 9:
Bài 1: Cho biểu thức
a. Rút gọn biểu thức
b. Tìm giá trị của
a) Rút gọn biểu thức
b) Tìm giá trị của để
a) Rút gọn biểu thức
b) Tìm giá trị của để
Bài 4: Rút gọn biểu thức:
Bài5: Cho các biểu thức:
a) Rút gọn biểu thức và
b) Tìm giá trị của để
Bài 6: Cho biểu thức:
a ) Rút gọn biểu thức
b) So sánh với
c) Với mọi giá trị của làm có nghĩa, chứng minh biểu thức
Bài 7: Cho biểu thức:
a ) Tìm điều kiện kèm theo để có nghĩa, rút gọn biểu thức ;
b) Tìm các số tự nhiên x để
c) Tính giá trị của với
Bài 8: Cho biểu thức :
a ) Rút gọn biểu thức ;
b/Tìm x để
Bài 9: Cho biểu thức :
a ) Rút gọn
b) Tìm a để
Bài 10: Cho biểu thức:
a ) Rút gọn
b) Tìm x để
c ) Tìm giá trị nhỏ nhất của
Bài 11: Cho biểu thức :
a ) Rút gọn
b) Tìm giá trị của để
Bài 12: Cho biểu thức :
a ) Rút gọn
b) Tìm các giá trị của để
c) Chứng minh
Bài 13: Cho biểu thức:
a ) Rút gọn
b) Tính theo
c) Xác định các giá trị của để tìm được ở câu b thoả mãn điều kiện
a ) Rút gọn
b) Tìm để
c ) Tìm giá trị nhỏ nhất của ?
Bài 15: Cho biểu thức:
a ) Rút gọn
b) Tính giá trị của nếu
c) Tìm giá trị nhỏ nhất của nếu
Bài 16: Cho biểu thức:
a ) Rút gọn
b) Với giá trị nào của thì
c) Với giá trị nào của thì
a ) Rút gọn
b) Tìm các giá trị của để
c) Tìm các giá trị của để
Bài 18: Cho biểu thức:
a ) Tìm điều kiện kèm theo để có nghĩa .b ) Rút gọn
c) Tính giá trị của khi a =
Bài 19: Cho biểu thức:
a ) Rút gọn
b) Chứng minh rằng
Bài 20: Cho biểu thức :
a ) Rút gọn
b) Tính
Bài 21: Cho biểu thức:
a ) Rút gọn
b) Tìm giá trị của để
Bài 22: Cho biểu thức :
a ) Rút gọn
b) Chứng minh P
Bài 23: Cho biểu thức :
a ) Rút gọn
b) Tính P khi
Bài 24: Cho biểu thức:
a ) Rút gọn
b) Cho
c) Chứng minh rằng
a ) Rút gọn
b) Với giá trị nào của thì
Bài 26: Cho biểu thức:
a ) Rút gọnb ) Tìm những giá trị nguyên của để có giá trị nguyên
Bài 27: Cho biểu thức:
a ) Rút gọn
b) Tìm giá trị của để
a ) Rút gọn
b) Cho
Bài 29: Cho biểu thức:
a ) Rút gọnb ) Tìm toàn bộ những số nguyên dương x để y = 625 và P Bài 30: Cho biểu thức:
Xem thêm: Cuộc sống vốn luôn chứa đựng những muộn phiền, cũng may còn có bầu trời luôn cho ta niềm tin!
a ) Rút gọn
b) So sánh với
Đại số 9 – Tags: biểu thức, rút gọn biểu thức, toán 9
Source: http://139.180.218.5
Category: tản mạn