Lý thuyết đường trung bình của tam giác, của hình thang>

1. Kiến thức cần nhớ 

Đường trung bình của tam giác

Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

Định lý 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

Định lý 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

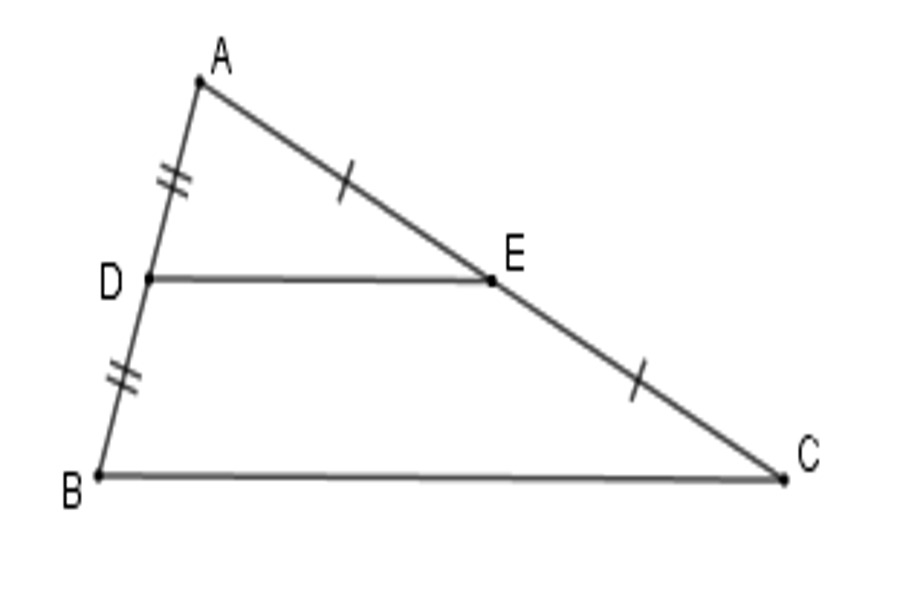
Ví dụ:

+ \ ( \ Delta ABC \ ) có \ ( D \ ) là trung điểm của \ ( AB \ ), \ ( E \ ) là trung điểm của \ ( AC \ ) nên \ ( DE \ ) là đường trung bình của tam giác \ ( ABC \ ) \ ( \ Rightarrow DE { \ rm { / / } } BC ; \, DE = \ dfrac { 1 } { 2 } BC. \ )+ Nếu \ ( \ left \ { \ begin { array } { l } DA = DB \ \ DE { \ rm { / / } } BC \ end { array } \ right. \ Rightarrow EC = EA \ ) .

Đường trung bình của hình thang

Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.

Định lí 3: Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.

Định lí 4: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

Ví dụ:

+ Hình thang \ ( ABCD \ ) ( hình vẽ ) có \ ( E \ ) là trung điểm \ ( AD \ ), \ ( F \ ) là trung điểm của \ ( BC \ ) nên \ ( EF \ ) là đường trung bình của hình thang \ ( \ Rightarrow \ left \ { \ begin { array } { l } EF { \ rm { / / } } DC \ \ EF = \ dfrac { { AB + DC } } { 2 } \ end { array } \ right. \ )

2. Các dạng toán thường gặp

Dạng 1: Chứng minh các hệ thức về cạnh và góc. Tính các cạnh và góc.

Phương pháp: 

Sử dụng đặc thù đường trung bình của tam giác và hình thang .+ Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy .+ Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy .

+ Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba .+ Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai .

Dạng 2: Chứng minh một cạnh là đường trung bình của tam giác, hình thang.

Phương pháp:

Sử dụng định nghĩa đường trung bình của tam giác và hình thang.

+ Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác .+ Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang .