Rate this post
Công thức tính thể tích chính là một trong những công thức toán học được áp dụng nhiều nhất vào đời sống thực tế. Đặt biệt là các công thức liên quan đến các khối lăng trụ, hình hộp,… Vậy bài viết ngay sau đây sẽ giới thiệu cho các bạn một công thức tính thể tích khối lăng trụ khá phổ biến trong cả toán học và áp dụng thực tế. Chính là công thức tính thể tích khối lăng trụ tam giác đều. Bên cạnh đó, bài viết còn đưa ra thêm một số ví dụ cụ thể để các bạn có thể dễ dàng áp dụng vào giải các bài toán liên quan.
Nội dung chính
Khối lăng trụ là gì?
Như thế nào là một khối lăng trụ?
Trước khi đi tìm hiểu về công thức tính thể tích khối lăng trụ đều là gì, chúng ta cùng nhau đi đến những khái niệm, định nghĩa về hình lăng trụ trước nhé! Vậy thế nào là một khối lăng trụ?
Theo như định nghĩa trong nghành toán học, hình lăng trụ chính là một đa diện đều mà hai đấy của nó phải là 2 đa giác bằng nhau ( đáy của khối lăng trụ hoàn toàn có thể là bất kể hình gì : hình vuông vắn, hình chữ nhật, hình tròn trụ, hình tam giác, hình bình hành, … ) và phải 2 đáp phải phân phối được điều kiện kèm theo cùng nằm trên 2 mặt phẳng song song nhau. Và đồng thời, những mặt bên còn lại của đa giác là hình bình hành và những cạnh bên hoặc là bằng, hoặc là song song với nhau .
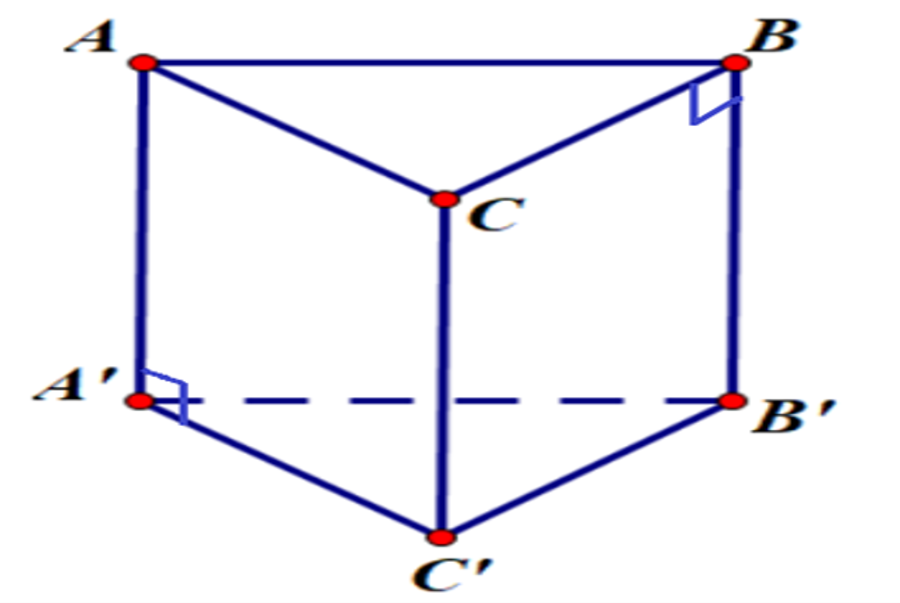
Các bạn hoàn toàn có thể thuận tiện tưởng tượng khối lăng trụ qua hình ảnh sau đây :
Phân loại khối lăng trụ:
Trong nghành toán học, người ta phân loại có 2 dạng khối lăng trụ chính :
Khối lăng trụ đứng,
Khối lăng trụ đứng chính là một trong những trường hợp đặt biệt của lăng trụ .
Nếu một khối lăng trụ thỏa mãn nhu cầu điều kiện kèm theo những cạnh bên của khối lăng trụ vuông góc với 2 dưới mặt đáy của nó thì được gọi là hình lăng trụ đứng .
Dựa theo khái niệm về hình lăng trụ đứng ở trên, ta hoàn toàn có thể phát biểu rằng trong trường hợp đó là một khối lăng trụ đứng thì những mặt bên của nó chính là hình chữ nhật .
Đây cũng chính là khối lăng trụ được sử dụng và áp dụng các công thức tính thể tích trên thực tế nhiều nhất. Công thức tính thể tích khối lăng trụ tam giác đều cũng nằm trong một trong số đó.
Nhận xét hình ảnh trên, ta thấy :
Canh bên AA ’ vuông góc với mặt phẳng đáy ( A’B ’ C ’ )
Cạnh bên BB ’ vuông góc với mặt phẳng đáy ( ABC )
Khối lăng trụ xiên (nghiêng):
Trái ngược trọn vẹn với định nghĩa khối lăng trụ đứng. Nếu như khối lăng trụ đứng đều có những cạnh bên song song và vuông góc với 2 đáy thì khối lăng trụ xiên lại là hình lăng trụ mà những cạnh bên của nó không vuông góc với 2 mặt phẳng đáy .
Nhận xét từ hình ảnh minh họa trên, ta thấy : độ dài chiều cao của khối lăng trụ xiên luôn nhỏ hơn so với độ dài của những cạnh bên .
Tham khảo thêm các công thức khác :
Tính chất và các khái niệm liên quan đến khối lăng trụ:
Một số tính chất của khối lăng trụ:
Biết được các tính chất của khối lăng trụ, ta có thể áp dụng công thức tính thể tích khối lăng trụ tam giác đều một các dễ dàng, nhanh chóng để đạt được hiệu quả cao hơn.
- Tính chất 1 : Một khối lăng trụ thì hai đáy của nó là 2 đa giác mà chúng nằm trên 2 mặt phẳng song song và đồng thời 2 đa giác đó đều bằng nhau .
- Tính chất 2 : Trong một khối lăng trụ thì tổng thể những cạnh bên của nó đều song song với nhau .
- Tính chất 3 : Tất cả những mặt bên của một khối lăng trụ đều là hình bình hành .
Một số khái niệm liên quan đến khối lăng trụ:
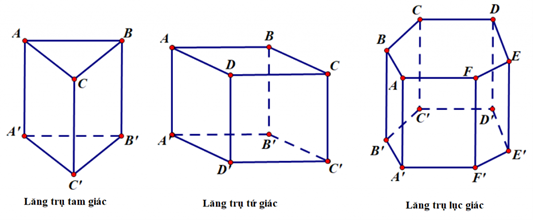
- Hình hộp chính là khối lăng trụ mà hai đáy của nó chính là hình bình hành .
- Khối lăng trụ tam giác đều là khối lăng trụ mà hai đáy của nó là hình tam giác .
- Khối lăng trụ tứ giác đều chính là khối lăng trụ mà 2 đáy của nó là hình vuông vắn .
- Khối lăng trụ ngũ giác đều là khối lăng trụ mà hai đáy của nó là hình ngũ giác .
-
Khối lăng trụ lục giác đều là khối lăng trụ mà 2 đáy của nó là hình lục giác.
Các khái niệm trên giúp ta phân biệt được đúng chuẩn những dạng của khối lăng trụ để hoàn toàn có thể vận dụng những công thức một cách đúng chuẩn .
Phía trên, bài viết có đề cập đến khối lăng trụ tam giác đều – chính là nhân vật chính trong bài viết. Vậy sau đây chúng ta cùng đi vào cụ thể tìm hiểu về khối lăng trụ tam giác đều cũng như công thức tính thể tích khối lăng trụ tam giác đều.
Khối lăng trụ đều, khối lăng trụ tam giác đều và các tính chất của nó:
Khối lăng trụ đều và khối lăng trụ tam giác đều:
Định nghĩa : khối lăng trụ đều là một trong những dạng lăng trụ đặc biệt quan trọng. Nếu một khối lăng trụ có hai đáy là 2 đa giác đều thì được gọi là khối lăng trụ đều .
Khối lăng trụ tam giác đều chính là một dạng khối lăng trụ đều thường gặp, với hai đáy của khối lăng trụ là hình tam giác đều .
Nhờ định nghĩa trên mà người ta rút ra được một số tính chất của khối lăng trụ đều, giúp ích trong việc áp dụng công thức tính thể tích khối lăng trụ tam giác đều.
Các tính chất của khối lăng trụ đều:
- Tính chất 1 : Tất cả những cạnh bên của khối lăng trụ đều thì luôn luôn vuông góc với 2 dưới mặt đáy .
- Tính chất 2 : Tất cả những cạnh bên của khối lăng trụ đều thì đều là hình chữ nhật .
- Tính chất thứ 3 : Hai đáy của một khối lăng trụ đều luôn luôn là những đa giác đều và bằng nhau → những cạnh đáy của khối lăng trụ đều thì đều bằng nhau .
Sau khi tìm hiểu chi tiết về tất cả các khái niệm cũng như tính chất về khối lăng trụ đều cũng như khối lăng trụ tam giác đều, chúng ta cùng đến với công thức tính thể tích khối lăng trụ tam giác đều.
Công thức tính thể tích khối lăng trụ tam giác đều:
Công thức tính thể tích khối lăng trụ tam giác đều:
Công thức tính thể tích khối lăng trụ tam giác đều là một công thức khá dễ để ghi nhớ cũng như áp dụng vào vận dụng bài tập hay ngay cả trong thực tế.
Đây là công thức chung để tính thể tích những khối lăng trụ đều, trong đó có khối lăng trụ tam giác đều :
V = S × h
Trong đó :
- S – là diện tích quy hoạnh mặt dưới ( hình tam giác đều ) của khối lăng trụ đều
- h – là độ dài chiều cao của khối lăng trụ ( tam giác ) đều .
Ví dụ, vận dụng công thức tính thể tích lăng trụ tam giác đều:
Bài tập 1: Hãy xác định thể tích của khối lăng trụ tam giác đều khi biết: Diện tích của mặt đáy hình tam giác đều của khối lăng trụ tam giác đều là 4 cm2 và chiều cao của khối lăng trụ đó là 3 cm.
Lời giải:
Tóm tắt, theo đề bài ta có :
S đáy (diện tích đáy hình tam giác đều) = 4 cm2
h (chiều cao của khối lăng trụ) = 3 cm
Dựa vào công thức tính thể tích khối lăng trụ tam giác đều, ta có:
V = S × h
→ V = 4 × 3
→ V = 12 ( cm3 )
→ Kết luận : Thể tích của khối lăng trụ tam giác đều trên là 12 cm3 .
Bài tập 2: Hãy cho biết thể tích của khối lăng trụ tam giác đều, biết: Cạnh đáy là 3 cm và chiều cao của khối lăng trụ tam giác đều là 2 cm.
Lời giải:
Ta có : h = 2 cm
Vì là khối lăng trụ tam giác đều → đáy là hình tam giác đều → những cạnh đáy đều bằng nhau = 3 cm
S đáy = 32 × 34
→ S đáy = 934 ( cm2 )
Áp dụng công thức tính thể tích khối lăng trụ tam giác đều ta có:
V = S × h
→ V = 934 × 2
→ V = 932 ( cm3 )
→ Kết luận : Thể tích của khối lăng trụ tam giác đều trên là : 932 ( cm3 )
Source: http://139.180.218.5
Category: tản mạn