Tính thể tích khối hộp – http://139.180.218.5

Bài viết trình diễn công thức tính thể tích khối hộp và 1 số ít ví dụ minh họa có giải thuật chi tiết cụ thể .

A. KIẾN THỨC CẦN NẮM VỮNG
Hình hộp: là hình lăng trụ tứ giác có đáy là hình bình hành.
Hình hộp có $6$ mặt là hình bình hành, $4$ đường chéo đồng qui tại tâm hình hộp.
Thể tích của khối hộp bằng tích số của diện tích mặt đáy và chiều cao của khối hộp đó.
Hình hộp chữ nhật: là hình hộp đứng và có đáy là hình chữ nhật.
Gọi $a$, $b$, $c$ là $3$ kích thước thì có đường chéo: $d = \sqrt {{a^2} + {b^2} + {c^2}} $, diện tích toàn phần: $S = 2(ab + bc + ca)$ và thể tích khối hộp chữ nhật: $V = abc.$
Hình lập phương: là hình hộp chữ nhật có $3$ kích thước bằng nhau.
Gọi $a$ là cạnh hình lập phương thì có đường chéo: $d = a\sqrt 3 $, diện tích toàn phần: $S = 6{a^2}$ và thể tích khối lập phương: $V = {a^3}.$

B. MỘT SỐ BÀI TOÁN ÁP DỤNG
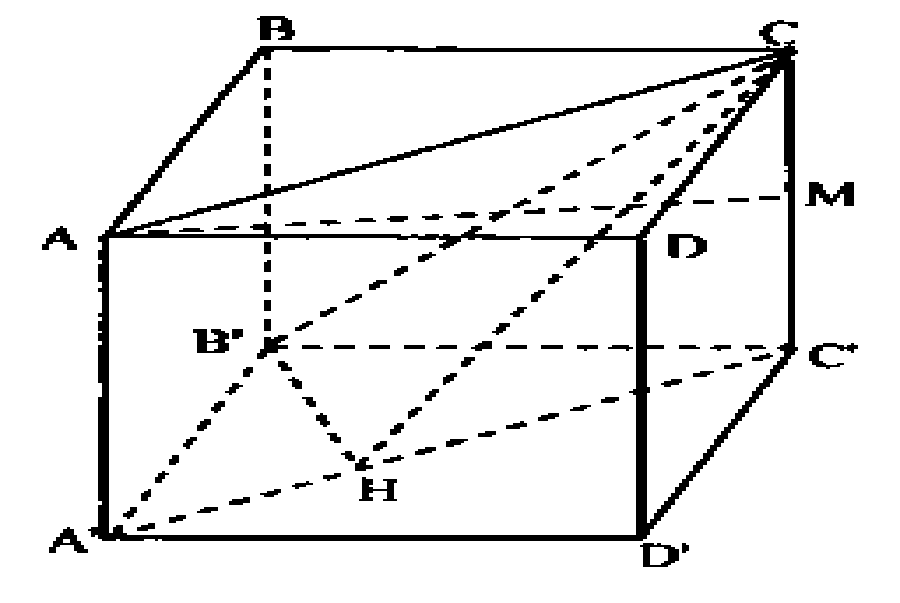
Bài toán 1: Tính thể tích của khối hộp $ABCD.A’B’C’D’$, biết rằng $AA’B’D’$ là khối tứ diện đều cạnh $a.$

Vì $AA’B’D’$ là tứ diện đều nên đường cao $AH$ của nó có hình chiếu $H$ là tâm của tam giác đều $A’B’D’.$
Suy ra: $A’H = \frac{{a\sqrt 3 }}{3}$, $AH = \sqrt {AA{‘^2} – A'{H^2}} = \frac{{a\sqrt 6 }}{3}.$
Ta có đáy $A’B’C’D’$ là hình thoi có góc $B’A’D’$ bằng $60°$ nên:
${S_{A’B’C’D’}} = A’B’.A’D’\sin {60^0} = \frac{{{a^2}\sqrt 3 }}{2}.$
Vậy thể tích khối hộp đã cho là: $V = S.h = \frac{{{a^2}\sqrt 3 }}{2} \cdot \frac{{a\sqrt 6 }}{3} = \frac{{{a^3}\sqrt 2 }}{2}.$

Bài toán 2: Cho khối hộp $ABCD.{A_1}{B_1}{C_1}{D_1}$ có tất cả các cạnh bằng nhau và bằng $a$, $\widehat {{A_1}AB} = \widehat {BAD} = \widehat {{A_1}AD} = \alpha $ $\left( {{0^0}

Hạ ${A_1}H \bot AC$ $(H \in AC).$
Tam giác ${A_1}BD$ cân (do ${A_1}B = {A_1}D$).
Suy ra $BD \bot {A_1}O.$
Mặt khác $BD \bot AC.$
Suy ra: $BD \bot \left( {{A_1}AO} \right)$ $ \Rightarrow BD \bot {A_1}H.$
Do đó ${A_1}H \bot (ABCD).$
Đặt $\widehat {{A_1}AD} = \varphi .$
Hạ ${A_1}K \bot AD$ $ \Rightarrow HK \bot AK$.
Ta có: $\cos \varphi .\cos \frac{\alpha }{2} = \frac{{AH}}{{A{A_1}}} \cdot \frac{{AK}}{{AH}} = \frac{{AK}}{{A{A_1}}}$ $ = \cos \varphi $ nên $\cos \varphi = \frac{{\cos \alpha }}{{\cos \frac{\alpha }{2}}}.$
Do đó: ${A_1}H = a\sin \varphi $ $ = a\sqrt {1 – \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\frac{\alpha }{2}}}} $ $ = \frac{a}{{\cos \frac{\alpha }{2}}}\sqrt {{{\cos }^2}\frac{\alpha }{2} – {{\cos }^2}\alpha } .$
${V_{ABCD.{A_1}{B_1}{C_1}{D_1}}} = AB.AD.\sin \alpha .{A_1}H$ $ = {a^2}\sin \alpha .\frac{a}{{\cos \frac{\alpha }{2}}}\sqrt {{{\cos }^2}\frac{\alpha }{2} – {{\cos }^2}\alpha } $ $ = 2{a^3}\sin \frac{\alpha }{2}\sqrt {{{\cos }^2}\frac{\alpha }{2} – {{\cos }^2}\alpha } .$

Bài toán 3: Cho khối hộp $ABCD.A’B’C’D’$ có đáy là hình chữ nhật với $AB = \sqrt 3 $, $AD = \sqrt 7 $ và các cạnh bên bằng $1.$ Hai mặt bên $(ABB’A’)$ và $(ADD’A’)$ lần lượt tạo với đáy những góc $45°$ và $60°.$ Hãy tính thể tích khối hộp.

Hạ $A’H \bot (ABCD)$, $HM \bot AD$, $HK \bot AB.$
Ta có: $AD \bot A’M$, $AB \bot A’K.$
$ \Rightarrow \widehat {A’MH} = {60^0}$, $\widehat {A’KH} = {45^0}.$
Đặt $A’H = x.$
Khi đó:
$A’M = x:\sin {60^0} = \frac{{2x}}{{\sqrt 3 }}.$
$AM = \sqrt {AA{‘^2} – A'{M^2}} $ $ = \sqrt {\frac{{3 – 4{x^2}}}{3}} = HK.$
Mà $HK = x\cot {45^0} = x$ nên $x = \sqrt {\frac{{3 – 4{x^2}}}{3}} \Rightarrow x = \sqrt {\frac{3}{7}} .$
Vậy ${V_{ABCD.A’B’C’D’}} = AD.AB.x = \sqrt 7 .\sqrt 3 .\sqrt {\frac{3}{7}} = 3.$

Bài toán 4: Cho khối lăng trụ tứ giác đều $ABCD.{A_1}{B_1}{C_1}{D_1}$ có khoảng cách giữa hai đường thẳng $AB$ và ${A_1}D$ bằng $2$ và độ dài đường chéo của mặt bên bằng $5.$
a) Hạ $AK \bot {A_1}D$ $\left( {K \in {A_1}D} \right).$ Chứng minh rằng: $AK = 2.$
b) Tính thể tích khối lăng trụ $ABCD.{A_1}{B_1}{C_1}{D_1}.$

a) $AB//{A_1}{B_1}$ $ \Rightarrow AB//\left( {{A_1}{B_1}D} \right).$
$ \Rightarrow d\left( {A,\left( {{A_1}{B_1}D} \right)} \right) = d\left( {AB,{A_1}D} \right).$
Ta có: ${A_1}{B_1} \bot \left( {A{A_1}{D_1}D} \right)$ $ \Rightarrow {A_1}{B_1} \bot AK.$
Mặt khác: ${A_1}D \bot AK$ $ \Rightarrow AK \bot \left( {{A_1}{B_1}D} \right).$
Vậy $AK = d\left( {A,\left( {{A_1}{B_1}D} \right)} \right) = d\left( {AB,{A_1}D} \right) = 2.$
b) Xét tam giác vuông ${A_1}AD$, ta có: $A{K^2} = {A_1}K.KD.$
Đặt ${A_1}K = x \Rightarrow 4 = x(5 – x)$ $ \Rightarrow {x^2} – 5x + 4 = 0$ $ \Rightarrow x = 1$ hoặc $x = 4.$
Với $x = 1$, $AD = \sqrt {A{K^2} + K{D^2}} = 2\sqrt 5 $, $A{A_1} = \sqrt {{A_1}{D^2} – A{D^2}} = \sqrt 5 .$
Khi đó ${V_{ABCD.{A_1}{B_1}{C_1}{D_1}}} = 20\sqrt 5 .$
Với $x = 4$, tương tự ta có: ${V_{ABCD.{A_1}{B_1}{C_1}{D_1}}} = 10\sqrt 5 .$

Bài toán 5: Cho hình hộp $ABCD.A’B’C’D’$ có tất cả các cạnh đều bằng $d$ và ba góc của đỉnh $A$ đều bằng $60°.$
a) Tính độ dài các đường chéo và thể tích $V$ của hình hộp.
b) Tính khoảng cách giữa hai mặt song song của hình hộp.
c) Có thể cắt hình hộp bằng một mặt phẳng sao cho thiết diện nhận được là một hình vuông?

a) Đặt $\overrightarrow {AA’} = \vec a$, $\overrightarrow {AB} = \vec b$, $\overrightarrow {AD} = \vec c$ thì $\vec a.\vec b = \vec b.\vec c = \vec c.\vec a = \frac{{{d^2}}}{2}.$
Ta có: $\overrightarrow {AC{‘^2}} = {(\vec a + \vec b + \vec c)^2}$ $ = {\vec a^2} + {\vec b^2} + {\vec c^2} + 2\vec a.\vec b + 2\vec b.\vec c + 2\vec c.\vec a = 6{d^2}.$
Suy ra: $AC’ = d\sqrt 6 .$
Ta có: ${\overrightarrow {BD’} ^2} = {(\overrightarrow a – \overrightarrow b + \overrightarrow c )^2}$ $ = {\vec a^2} + {\vec b^2} + {\vec c^2} – 2\vec a.\vec b – 2\vec b.\vec c + 2\vec c.\vec a = 2{d^2}.$
Suy ra: $BD’ = d\sqrt 2 .$
Tương tự $DB’ = CA’ = d\sqrt 2 $ nên ta có $AA’BD$ là hình tứ diện đều cạnh $d$, nên: ${V_{\left( {AA’BD} \right)}} = \frac{{{d^3}\sqrt 2 }}{{12}}.$
Do đó $V = 6{V_{AA’BD}} = \frac{{{d^3}\sqrt 2 }}{{12}}.$
b) Gọi $h$ là khoảng cách giữa hai mặt phẳng $(ABCD)$ và $(A’B’C’D’)$ thì:
$V = {S_{ABCD}}.h = \frac{{{d^2}\sqrt 3 }}{2}$ $ \Rightarrow h = \frac{{d\sqrt 6 }}{2}.$
Tương tự thì các khoảng cách giữa hai mặt song song nào cũng bằng $\frac{{d\sqrt 6 }}{2}.$
c) Hình bình hành $BCD’A’$ có các cạnh bằng $d$ và hai đường chéo bằng $d\sqrt 2 $ nên nó là hình vuông.
Vậy hình hộp có thiết diện $BCD’A’$ là hình vuông.
Tương tự thiết diện $CDA’B’$ cũng là hình vuông.

Bài toán 6: Cho hình lăng trụ $ABCD.A’B’C’D’$ có đáy là hình vuông cạnh bằng $a\sqrt 3 $, $A$ cách đều $A$, $B$, $C$, $D.$ Biết rằng khoảng cách từ trọng tâm $G$ của tam giác $AB’D’$ đến mặt phẳng $(AA’D’)$ bằng $\frac{a}{2}.$ Tính thể tích khối lăng trụ đã cho và khoảng cách từ tâm $O$ của hình vuông $A’B’C’D’$ đến mặt phẳng $(ADC’B’).$

Vì $G$ là trọng tâm của tam giác $AB’D’$ nên $G$ nằm trên đoạn thẳng $AO$ và $AG = \frac{2}{3}AO.$
Ta có: $d\left( {O;\left( {AA’D} \right)} \right) = \frac{3}{2}d(G,(AA’D)) = \frac{{3a}}{4}.$
Gọi $M$ là trung điểm của $A’D’.$
Hạ $OH \bot AM$ thì $OH \bot \left( {AA’D’} \right).$
Do đó $OH = d\left( {O;\left( {AA’D’} \right)} \right) = \frac{{3a}}{4}.$
Tam giác $AOM$ vuông tại $O:$
$\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{M^2}}}$ $ \Leftrightarrow \frac{{16}}{{9{a^2}}} = \frac{1}{{O{A^2}}} + \frac{4}{{3{a^2}}}$ $ \Rightarrow OA = \frac{{3a}}{2}.$
Vậy ${V_{ABCD.A’B’C’D’}} = {S_{ABCD}}.OA = 3{a^2}.\frac{{3a}}{2} = \frac{{9{a^3}}}{2}.$
Gọi $N$ là trung điểm của $B’C’.$ Hạ $OK \bot AN.$
Ta có $OK \bot \left( {ADC’B’} \right)$ nên $OK = d\left( {O,\left( {ADC’B’} \right)} \right).$
Tam giác $AON$ vuông tại $O:$
$\frac{1}{{O{K^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{N^2}}}$ $ = \frac{4}{{9{a^2}}} + \frac{4}{{3{a^2}}} = \frac{{16}}{{9{a^2}}}$ $ \Rightarrow OK = \frac{{3a}}{4}.$
Vậy khoảng cách từ tâm $O$ của hình vuông $A’B’C’D’$ đến mặt phẳng $(ADC’B’)$ là $OK = \frac{{3a}}{4}.$

Bài toán 7: Cho hình hộp $ABCD.A’B’C’D’$ có đáy là hình chữ nhật. $AB = a\sqrt 3 $, $AA’ = AC = 2a\sqrt 3 .$ Hình chiếu của $B$ lên mặt phẳng $(A’B’C’D’)$ là trung điểm $O$ của $B’D’.$ Tính thể tích khối hộp $ABCD.A’B’C’D’$ và cosin của góc giữa hai đường thẳng $AC$ và $BB’.$

Ta có $O$ là tâm của hình chữ nhật $A’B’C’D’$ nên $BO \bot \left( {A’B’C’D’} \right).$
Tam giác vuông $ABC:$
$BC = \sqrt {A{C^2} – A{B^2}} $ $ = \sqrt {12{a^2} – 3{a^2}} = 3a.$
Tam giác vuông $BOB’$ ta có:
$BO = \sqrt {BB{‘^2} – B'{O^2}} $ $ = \sqrt {BB{‘^2} – \frac{{A{C^2}}}{4}} $ $ = \sqrt {12{a^2} – 3{a^2}} = 3a.$
Nên ${V_{ABCD.A’B’C’D’}} = {S_{ABCD}}.BO = AB.BC.BO$ $ = a\sqrt 3 .3a.3a = 9{a^3}\sqrt 3 .$
Ta có $\cos \left( {AC,BB’} \right) = \cos \left( {A’C’,AA’} \right) = \left| {\cos \widehat {AA’O}} \right|.$
Vì $BO \bot (ABCD) \Rightarrow BO \bot AB.$
Tam giác $ABO$ vuông cân tại $B:$ $AO = \sqrt {A{B^2} + B{O^2}} $ $ = \sqrt {3{a^2} + 9{a^2}} = 2a\sqrt 3 .$
Áp dụng định lý cosin trong tam giác $AA’O$ ta có:
$\cos \widehat {AA’O} = \frac{{A'{A^2} + A'{O^2} – A{O^2}}}{{2A’A.A’O}}$ $ = \frac{{12{a^2} + 3{a^2} – 12{a^2}}}{{2.2a\sqrt 3 .a\sqrt 3 }} = \frac{1}{4}.$
Vậy $\cos \left( {AC,BB’} \right) = \frac{1}{4}.$

Bài toán 8: Cho hình hộp đứng $ABCD.A’B’C’D’$ có đáy là hình bình hành, $AB = 2a$, $BC = a$, $\widehat {BAD} = {60^0}$, góc giữa đường thẳng $B’C$ và mặt phẳng $(ACC’A’)$ bằng $30°.$ Tính thể tích khối hộp $ABCD.A’B’C’D’$ và khoảng cách giữa hai đường thẳng $AM$, $DD’$ với $M$ là trung điểm của $CC’.$

Hạ $BH \bot A’C’$ thì có $BH \bot \left( {ACC’A’} \right).$
Từ đó suy ra góc giữa $B’C$ và mặt phẳng $\left( {ACC’A’} \right)$ bằng $\widehat {B’CH}.$
Áp dụng định lý côsin trong tam giác $ABC$ ta có:
$A{C^2} = B{C^2} + B{A^2} – 2.BC.BA\cos {120^0}$ $ = {a^2} + 4{a^2} – 2a.2a\left( { – \frac{1}{2}} \right) = 7{a^2}.$
Suy ra $AC = a\sqrt 7 .$
Ta có: $B’H = \frac{{2{S_{A’B’C’}}}}{{A’C’}} = \frac{{B’A’.B’C’.\sin {{120}^0}}}{{A’C’}}$ $ = \frac{{a.2a.\frac{{\sqrt 3 }}{2}}}{{a\sqrt 7 }} = \frac{{a\sqrt {21} }}{7}.$
Tam giác vuông $B’CH:$ $B’C = \frac{{B’H}}{{\sin {{30}^0}}} = \frac{{2a\sqrt {21} }}{7}.$
Tam giác vuông $BB’C:$ $BB’ = \sqrt {B'{C^2} – B{C^2}} $ $ = \sqrt {\frac{{84{a^2}}}{{49}} – {a^2}} = \frac{{a\sqrt {35} }}{7}.$
Nên: ${V_{ABCD.A’B’C’D’}} = AB.AD\sin {60^0}.AA’$ $ = 2a.a.\frac{{\sqrt 3 }}{2}.\frac{{a\sqrt {35} }}{7} = \frac{{{a^3}.\sqrt {105} }}{7}.$
Ta có $AM$ song song với $(ACC’A’).$
Do đó $d\left( {DD’,AM} \right)$ $ = d\left( {DD’,\left( {ACC’A’} \right)} \right)$ $ = d\left( {D’,\left( {ACC’A’} \right)} \right)$ $ = d\left( {B’,\left( {ACC’A’} \right)} \right)$ $ = B’H = \frac{{a\sqrt {21} }}{7}.$