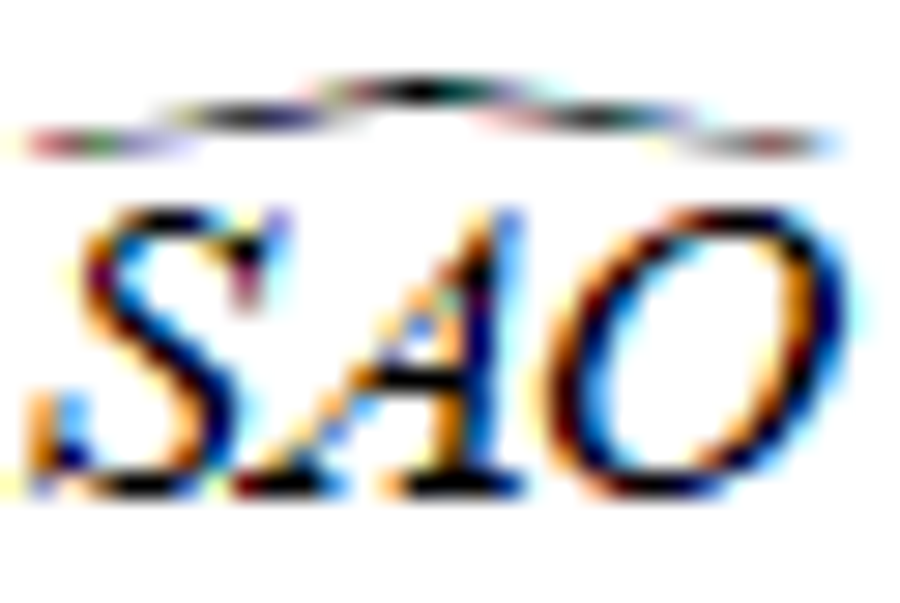Thể tích khối nón tròn xoay, cụt chi tiết từ A – Z có ví dụ minh họa

Trong bài viết dưới đây, điện máy Sharp Việt Nam tiếp tục giới thiệu và chia sẻ công thức tính thể tích khối nón, tròn xoay, cụt và các dạng bài tập từ cơ bản đến nâng cao có lời giải chi tiết các bạn cùng tham khảo nhé

Công thức tính thể tích khối nón

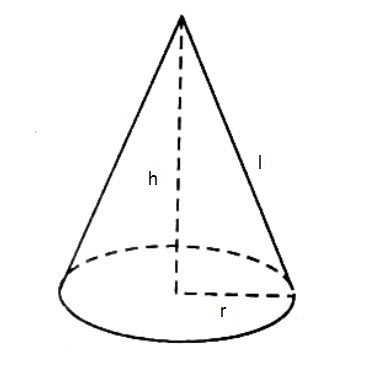
Thể tích khối nón bằng 1/3 tích của số pi, độ cao và bình phương nửa đường kính đáy của hình nón

V = 1/3Bh = 1/3πr2h

Trong đó :

• B là diện tích đáy hình nón
• r là bán kính đáy hình nón
• h là chiều cao hình nón
• π: là hằng số Pi = 3,14

Các xác lập đường sinh, đường cao và nửa đường kính đáy

Do hình nón được tạo thành khi quay một tam giác vuông quanh trục một cạnh góc vuông của nó một vòng, nên hoàn toàn có thể coi đường cao và nửa đường kính đáy là 2 cạnh góc vuông của tam giác, còn đường sinh là cạnh huyền .
Do đó, khi biết đường cao và nửa đường kính đáy, ta hoàn toàn có thể tính được đường sinh bằng công thức :

l = √r2 + h2

Biết nửa đường kính và đường sinh, tính đường cao theo công thức :

h = √l2 – r2

Biết đường cao và đường sinh, tính nửa đường kính đáy theo công thức :

r = √l2 – h2

Công thức tính thể tích khối nón tròn xoay

Thể tích của khối nón tròn xoay cũng tựa như như thể tích khối nón bằng 1/3 tích của bình phương nửa đường kính đáy, độ cao và hằng số pi

V = 1/3Bh = 1/3πr2h

Trong đó :

• B là diện tích đáy hình nón
• r là bán kính đáy hình nón
• h là chiều cao hình nón
• π: là hằng số Pi = 3,14

Thể tích khối nón cụt ( hình nón cụt )

Thể tích hình nón cụt bằng hiệu thể tích của hình nón lớn và hình nón nhỏ

V = 1/3π.(r12 + r22 + r1.r2).h

Trong đó :

• V là thể tích hình
• r1, r2 là bán kính 2 đáy của hình nón cụt.
• h là chiều cao khoảng cách giữa 2 đáy của hình nón cụt.
• π: số Pi (3.14159265).

Các bạn có thể tham khảo thêm:

Bài tập tính thể tích khối nón tròn xoay và cụt

Ví dụ 1 : Cho hình nón tròn xoay có đỉnh là S ; O là tâm của đường tròn đáy, đường sinh bằng a √ 2 và góc giữa đường sinh và mặt phẳng đáy bằng 60 độ. Tính diện tích quy hoạnh xung quanh của hình nón và thể tích lần lượt là ?

Lời giải:

Gọi A là một điểm thuộc đường tròn đáy hình nón .

Theo giải thiết ta có đường sinh SA = a√2 và góc giữa đường sinh và mặt phẳng đáy là   = 600 .

Trong tam giác vuôn SAO, ta có :

Diện tích xung quanh hình nón là :

Thể tích của khối nón tròn xoay

Chọn đáp án A
Ví dụ 2 : Tính diện tích quy hoạnh xung quanh, diện tích quy hoạnh toàn phần hình nón, tính thể tích khối nón cực hay. a √ 2 = πR2Ví dụ 2. Một hình nón có đường kính đáy là 2 a √ 3, góc ở đỉnh là 120 độ. Tính V của khối nón đó theo a .

Lời giải :

Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.

Theo giả thiết dễ suy ra đường tròn đáy có nửa đường kính là :

Xét tam giác SAO vuông tại O, ta có :

Do đó chiều cao hình nón là h = SO = a .
Vậy thể tích khối nón là

Chọn đáp án B
Ví dụ 3 : Cho hình tròn trụ có nửa đường kính bằng 6. Cắt bỏ 1/4 hình tròn trụ giữa hai nửa đường kính OA và OB, rồi ghép hai nửa đường kính đó lại sao cho hình thành một hình nón ( hình vẽ ). Tính V khối nón tương ứng

Lời giải :

Diện tích hình tròn trụ có nửa đường kính bằng R = 6 là :

Cắt bỏ 1/4 hình tròn trụ thì diện tích quy hoạnh còn lại chính là diện tích quy hoạnh xung quanh của nón. Đường sinh của nón là nửa đường kính đường tròn : l = R = 6
Diện tích xung quanh của nón là :

Khi đó, đường cao hình nón là

Thể tích khối nón tương ứng là

Chọn đáp án A .
Ví dụ 4 : Cho hình nón cụt có đường kính hai dưới mặt đáy lần lượt là 12 cm và 18 cm. Chiều cao nối giữa hai mặt đáy dài 7 cm. Tính thể tích hình nón cụt .
Lời giải :
Đường kính hai dưới mặt đáy lần lượt là 12 cm và 18 cm .

Hy vọng với những thông tin mà chúng tôi vừa san sẻ phía trên hoàn toàn có thể giúp bạn nắm rõ được những công thức tính thể tích hình nón, thể tích hình nón tròn xoay và thể tích hình nón cụt vận dụng giải những bài tập cơ bản hoặc nâng cao nhanh gọn

5/5 – ( 1 bầu chọn )