Thể Tích Và Diện Tích: Hình Trụ Tròn — Bảng Tính Trực Tuyến, Công Thức

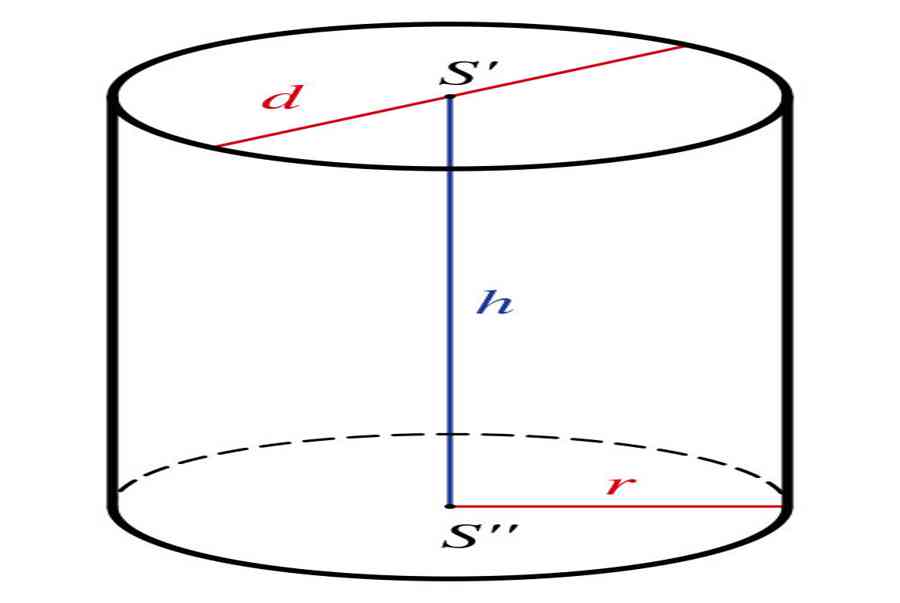
Công thức tính thể tích hình trụ tròn là \(\)\(V = πr^2h\), và công thức tính diện tích hình trụ tròn là \(A = 2πr^2 + 2πrh = 2πr(r + h)\). Giờ đây, bạn có thể tính thể tích và diện tích hình trụ tròn online với bảng tính của HocTapHay.Com, giúp tính toán nhanh kết quả và chính xác nhất.

Hãy Đưa Ra Chiều Cao h Và 1 Giá Trị

h =
r =
d =

Làm tròn số thập phân

Thể tích V =
Diện tích A =
Diện tích đáy \(A_d =\)
Diện tích xung quanh \(A_{xq} =\)

\ ( V = πr ^ 2 h \ )
\ ( A_d = πr ^ 2 \ )
\ ( A_ { xq } = 2. πrh \ )
\ ( A = 2. A_d + A_ { xq } \ )
\ ( A = 2. πr ( r + h ) \ )
\ ( d = 2. r \ )

Trong đó:

• V: thể tích
• A: diện tích
• \(A_d\): diện tích đáy
• \(A_{xq}\): diện tích xung quanh
• r: bán kính
• d: đường kính
• h: đường cao
• S’, S”: tâm đáy

1. Mặt Trụ Tròn Xoay

Trong mp ( P. ) cho hai đường thẳng Δ và l song song nhau, cách nhau một khoảng chừng r. Khi quay mp ( P. ) quanh trục cố định và thắt chặt Δ thì đường thẳng l sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay hay gọi tắt là mặt trụ .
– Đường thẳng Δ được gọi là trục .
– Đường thẳng l được gọi là đường sinh .
– Khoảng cách r được gọi là nửa đường kính của mặt trụ .

2. Hình Trụ Tròn Xoay

Khi quay hình chữ nhật ABCD xung quanh đường thẳng chứa một cạnh, ví dụ điển hình cạnh AB thì đường gấp khúc ABCD tạo thành một hình, hình đó được gọi là hình tròn trụ tròn xoay hay gọi tắt là hình tru .
– Đường thẳng AB được gọi là trục .
– Đoạn thẳng CD được gọi là độ dài đường sinh .
– Độ dài đoạn thẳng AB = CD = h được gọi là chiều cao của hình tròn trụ .
– Hình tròn tâm A, nửa đường kính r = AD và hình tròn trụ tâm B, nửa đường kính r = BC được gọi là 2 đáy của hình tròn trụ .
– Khối trụ tròn xoay, gọi tắt là khối trụ, là phần khoảng trống số lượng giới hạn bởi hình tròn trụ tròn xoay kể cả hình tròn trụ .

3. Công Thức Tính Diện Tích Và Thể Tích Của Hình Trụ

Cho hình tròn trụ có chiều cao là h và nửa đường kính đáy bằng r, khi đó :
– Diện tích xung quanh của hình tròn trụ : \ ( S_ { xq } = 2 πrh \ )
– Diện tích toàn phần của hình tròn trụ : \ ( S_ { tp } = S_ { xq } + 2. S_ { đáy } = 2 πrh + 2 πr ^ 2 \ )
– Thể tích khối trụ : \ ( V = B.h = πr ^ 2 h \ )

4. Tính Chất

– Nếu cắt mặt trụ tròn xoay ( có nửa đường kính là r ) bởi một mp ( α ) vuông góc với trục Δ thì ta được đường tròn có tâm trên Δ và có nửa đường kính bằng r với r cũng chính là nửa đường kính của mặt trụ đó .
– Nếu cắt mặt trụ tròn xoay ( có nửa đường kính là r ) bởi một mp ( α ) không vuông góc với trục Δ nhưng cắt toàn bộ những đường sinh, ta được giao tuyến là một đường elíp có trụ nhỏ bằng 2 r và trục lớn bằng \ ( \ frac { 2 r } { sinφ } \ ), trong đó φ là góc giữa trục Δ và mp ( α ) với \ ( 0 ^ 0 + Nếu d > r thì mp(α) không cắt mặt trụ.

5. Dạng Toán

Dạng 1: Cho các dữ kiện như r, h để tính S, V hoặc ngược lại.

Phương pháp giải: Xác định các yếu tố đề bài đã cho của hình trụ, khối trụ kết hợp với các công thức đã biết từ đó tìm các yếu tố chưa biết và giải quyết bài toán.

Cho hình tròn trụ có chiều cao là h và nửa đường kính đáy bằng r ( đường cao bằng đường sinh : h = l ) khi đó :
– Diện tích xung quanh của hình tròn trụ : \ ( S_ { xq } = 2 πrh \ )
– Diện tích toàn phần của hình tròn trụ : \ ( S_ { tp } = S_ { xq } + 2. S_ { đáy } = 2 πrh + 2 πr ^ 2 \ )
– Thể tích khối trụ : \ ( V = B.h = πr ^ 2 h \ )

Dạng 2: Tương giao giữa hình trụ và mặt phẳng, đường thẳng

Phương pháp giải:

– Thiết diện qua trục là hình chữ nhật hoặc hình vuông vắn có 1 cạnh bằng chiều cao của hình tròn trụ và 1 cạnh bằng 2 lần nửa đường kính của đáy trụ .
– Cách xác lập góc giữa đường thẳng và trục của hình tròn trụ .

Dạng 3: Sự tạo thành mặt trụ, hình trụ

Phương pháp giải: Học sinh nắm chắc sự tạo thành mặt trụ, hình trụ, khối trụ (sgk/35).

Dạng 4: Hình trụ nội tiếp, ngoại tiếp hình lập phương, hình lăng trụ, hình hộp, mặt cầu, hình nón.

Phương pháp giải: Dùng định nghĩa hình trụ nội tiếp, ngoại tiếp của một hình.

Phép Tính Liên Quan

Hình Cầu
Hình Chóp Hình Hộp Chữ Nhật Hình Lăng Trụ
Hình Nón Hình Trụ Tròn Khối Lập Phương

5/5 ( 1 bầu chọn )