Khoảng cách từ một điểm tới một mặt phẳng – http://139.180.218.5

Bài viết hướng dẫn cách xác lập và tính khoảng cách từ một điểm đến một mặt phẳng trong khoảng trống, đây là dạng toán thường gặp trong chương trình Hình học 11 chương 3 : Quan hệ vuông góc, kiến thức và kỹ năng và các ví dụ trong bài viết được tìm hiểu thêm từ các tài liệu hình học khoảng trống được đăng tải trên TOANMATH.com.

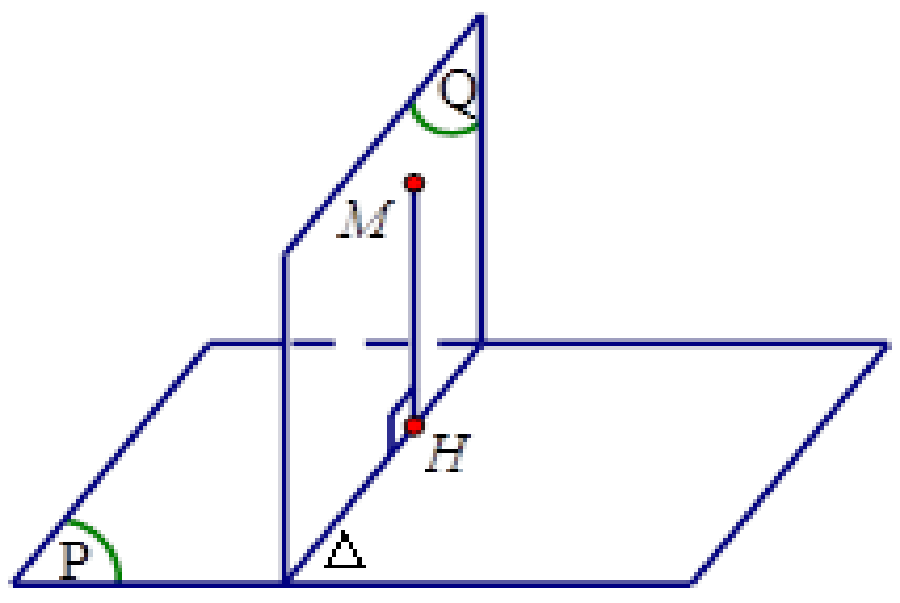
Bài toán: Xác định khoảng cách từ điểm $M$ đến mặt phẳng $(P).$

Để xác lập khoảng cách từ điểm USD M $ đến mặt phẳng USD ( P. ) USD, ta sử dụng các chiêu thức sau đây :

Phương pháp 1
+ Tìm mặt phẳng $(Q)$ chứa $M$ và vuông góc với mặt phẳng $(P)$ theo giao tuyến $∆.$
+ Từ $M$ hạ $MH$ vuông góc với $∆$ ($H ∈ Δ$).
+ Khi đó $d(M,(P)) = MH.$

Ví dụ 1: Cho hình chóp đều $S.ABC$, đáy $ABC$ có cạnh bằng $a$, mặt bên tạo với đáy một góc $α$. Tính $d(A,(SBC))$ theo $a$ và $α.$

Gọi $I$ là trung điểm của $BC.$
+ Ta có: $\left. \begin{array}{l}
SI \bot BC\\
AI \bot BC
\end{array} \right\} \Rightarrow BC \bot (SAI)$ và $\widehat {SIA} = \alpha .$
+ Kẻ $AH \bot SI{\rm{ (H}} \in {\rm{SI)}}$ mà $SI = (SAI) \cap (SBC)$ nên $AH \bot (SBC)$. Do đó, $d(A,(SBC)) = AH.$
+ Mặt khác, xét tam giác vuông $AHI$ có: $AH = AI.\sin \alpha = \frac{{a\sqrt 3 }}{2}.\sin \alpha .$
Vậy: $d(A,(SBC)) = AH = \frac{{a\sqrt 3 }}{2}.\sin \alpha .$

Ví dụ 2: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình vuông cạnh $a$, $SA \bot (ABCD)$, $SA=2a.$
a) Tính $d(A,(SBC))$.
b) Tính $d(A,(SBD))$.

a) Kẻ $AH \bot SB{\rm{ (H}} \in {\rm{SB) (1)}}.$
Ta có: $SA \bot (ABCD) \Rightarrow SA \bot BC{\rm{ (*)}}$ và $AB \bot BC{\rm{ (gt) (**)}}$. Từ $(*)$ và $(**)$ suy ra: $BC \bot (SAB) \Rightarrow {\rm{BC}} \bot {\rm{AH (2)}}.$
Từ $(1)$ và $(2)$ ta có: $AH \bot (SBC)$ hay $d(A,(SBC)) = AH.$
+ Mặt khác, xét tam giác vuông $SAB$ có: $\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{S{A^2}}} = \frac{5}{{4{a^2}}}$ $ \Rightarrow AH = \frac{{2a}}{{\sqrt 5 }}.$
Vậy $d(A,(SBC)) = \frac{{2a}}{{\sqrt 5 }}.$
b) Gọi $O = AC \cap BD.$
Kẻ $AK \bot SB{\rm{ (K}} \in {\rm{SO) (1)}}.$
Ta có: $SA \bot (ABCD) \Rightarrow SA \bot BD{\rm{ (*)}}$ và $AC \bot BD{\rm{ (gt) (**)}}$. Từ $(*)$ và $(**)$ suy ra: $BD \bot (SAC) \Rightarrow {\rm{BC}} \bot {\rm{AK (2)}}.$
Từ $(1)$ và $(2)$ ta có: $AK \bot (SBD)$ hay $d(A,(SBD)) = AK.$
+ Mặt khác, xét tam giác vuông $SAO$ có: $\frac{1}{{A{K^2}}} = \frac{1}{{A{O^2}}} + \frac{1}{{S{A^2}}} = \frac{9}{{4{a^2}}}$ $ \Rightarrow AK = \frac{{2a}}{3}.$
Vậy $d(A,(SBD)) = \frac{{2a}}{3}.$

Ví dụ 3: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình vuông cạnh $a$, tam giác $SAB$ đều, $(SAB) \bot (ABCD)$. Gọi $I, F$ lần lượt là trung điểm của $AB$ và $AD$. Tính $d(I,(SFC)).$

Gọi $K = FC \cap ID.$
+ Kẻ $IH \bot SK{\rm{ (H}} \in {\rm{K) (1)}}.$
+ Ta có:
$\left. \begin{array}{l}
(SAB) \bot (ABCD)\\
(SAB) \cap (ABCD) = AB\\
SI \subset (SAB)\\
SI \bot AB
\end{array} \right\}$ $ \Rightarrow SI \bot (ABCD).$
$ \Rightarrow SI \bot FC{\rm{ (*)}}.$
+ Mặt khác, xét hai tam giác vuông $AID$ và $DFC$ có: $AI = DF$, $AD = DC.$
Suy ra $\Delta AID = \Delta DFC$ $ \Rightarrow \widehat {AID} = \widehat {DFC},\widehat {ADI} = \widehat {DCF}.$
Mà $\widehat {AID} + \widehat {ADI} = {90^0}$ $ \Rightarrow \widehat {DFC} + \widehat {ADI} = {90^0}.$
Hay $FC \bot ID$ $(**).$
+ Từ $(*)$ và $(**)$ ta có: $FC \bot (SID) \Rightarrow IH \bot FC$ $(2)$. Từ $(1)$ và $(2)$ suy ra: $IH \bot (SFC)$ hay $d(I,(SFC)) = IH.$
+ Ta có:
$SI = \frac{{a\sqrt 3 }}{2},ID = \frac{{a\sqrt 5 }}{2},$ $\frac{1}{{D{K^2}}} = \frac{1}{{D{C^2}}} + \frac{1}{{D{F^2}}} = \frac{5}{{{a^2}}}$ $ \Rightarrow DK = \frac{{a\sqrt 5 }}{5}$ $ \Rightarrow IK = ID – DK = \frac{{3a\sqrt 5 }}{{10}}.$
Do đó $\frac{1}{{I{H^2}}} = \frac{1}{{S{I^2}}} + \frac{1}{{I{K^2}}} = \frac{{32}}{{9{a^2}}}$ $ \Rightarrow IH = \frac{{3a\sqrt 2 }}{8}.$
Vậy $d(I,(SFC)) = \frac{{3a\sqrt 2 }}{8}.$

Phương pháp 2
+ Qua $M$, kẻ $∆ // (P)$. Ta có: $d(M,(P)) = d(∆,(P)).$
+ Chọn $N \in \Delta $. Lúc đó ${\rm{d}}\left( {{\rm{M}},\left( {\rm{P}} \right)} \right) = {\rm{d}}(\Delta ,{\rm{(P)) = d}}\left( {N,\left( {\rm{P}} \right)} \right)$.

Ví dụ 4: Cho lăng trụ $ABCD.A’B’C’D’$, $ABCD$ là hình chữ nhật, $AB = a,AD = a\sqrt 3$. Hình chiếu vuông góc của $A’$ trên $(ABCD)$ trùng với giao điểm của $AC$ và $BD$. Tính $d(B’,(A’BD)).$

+ Gọi $O$ là giao điểm của $AC$ và $BD.$ Vì $B’C//A’D$ nên $B’C//(A’BD)$. Do đó: $d(B’,(A’BD)) = d(B’C,(A’BD))$ $ = d(C,(A’BD)).$
+ Trong mặt phẳng $(ABCD)$ kẻ $CH \bot BD,{\rm{ (H}} \in {\rm{BD) (1)}}$. Mặt khác $A’O \bot (ABCD)$ $ \Rightarrow A’O \bot CH{\rm{ (2)}}.$
Từ $(1)$ và $(2)$ suy ra: $CH \bot (A’BD)$ $ \Rightarrow d(B’,(A’BD)) = CH.$
+ Xét tam giác vuông $BCD$ có: $\frac{1}{{C{H^2}}} = \frac{1}{{B{C^2}}} + \frac{1}{{C{D^2}}} = \frac{4}{{3{a^2}}}$ $ \Rightarrow CH = \frac{{a\sqrt 3 }}{4}.$
Vậy: $d(B’,(A’BD)) = CH = \frac{{a\sqrt 3 }}{4}.$

Ví dụ 5: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $\widehat {ABC} = {30^0}$, $\Delta SBC$ là tam giác đều cạnh $a$, $(SBC) \bot (ABC)$. Tính $d(C,(SAB))$.

+ Trong mặt phẳng $(ABC)$ vẽ hình chữ nhật $ABDC$. Gọi $M, I, J$ lần lượt là trung điểm của $BC, CD$ và $AB$. Lúc đó, $CD // (SAB)$ hay: $d(C,(SAB)) = d(CD,(SAB))$ $ = d(I,(SAB)).$
+ Trong mặt phẳng $(SIJ)$ kẻ $IH \bot SJ,{\rm{ (H}} \in {\rm{SJ) (1)}}.$
Mặt khác, ta có: $\left. \begin{array}{l}
IJ \bot AB\\
SM \bot (ABC) \Rightarrow AB \bot SM
\end{array} \right\}$ $ \Rightarrow AB \bot (SIJ) \Rightarrow AB \bot IH{\rm{ (2)}}.$
Từ $(1)$ và $(2)$ suy ra: $IH \bot (SAB)$ hay $d(C,(SAB)) = IH.$
+ Xét tam giác $SIJ$ có: ${S_{SIJ}} = \frac{1}{2}IH.SJ = \frac{1}{2}SM.IJ$ $ \Rightarrow IH = \frac{{SM.IJ}}{{SJ}}.$
Với: $IJ = AC = BC.\sin {30^0} = \frac{a}{2}$, $SM = \frac{{a\sqrt 3 }}{2}$, $SJ = \sqrt {S{M^2} + M{J^2}} = \frac{{a\sqrt {13} }}{4}$.
Do đó: $IH = \frac{{SM.IJ}}{{SJ}} = \frac{{a\sqrt {39} }}{{13}}.$
Vậy $d(C,(SAB)) = \frac{{a\sqrt {39} }}{{13}}.$

Phương pháp 3
+ Nếu $MN \cap (P) = I$. Ta có: $\frac{{{\rm{d}}\left( {{\rm{M}},\left( {\rm{P}} \right)} \right)}}{{{\rm{d}}\left( {N,\left( {\rm{P}} \right)} \right)}} = \frac{{MI}}{{NI}}$.
+ Tính ${\rm{d}}\left( {N,\left( {\rm{P}} \right)} \right)$ và $\frac{{MI}}{{NI}}$.
+ ${\rm{d}}\left( {{\rm{M}},\left( {\rm{P}} \right)} \right) = \frac{{MI}}{{NI}}.{\rm{d}}\left( {N,\left( {\rm{P}} \right)} \right)$.

Chú ý : Điểm $ N $ ở đây ta phải chọn sao cho tìm khoảng cách từ $ N $ đến mặt phẳng USD ( P. ) USD dễ hơn tìm khoảng cách từ USD M $ đến mặt phẳng USD ( P. ). $

Ví dụ 6: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $D$, $AB = AD = a$, $CD = 2a$, $SD \bot (ABCD)$, $SD = a.$
a) Tính $d(D,(SBC)).$
b) Tính $d(A,(SBC)).$

Gọi $M$ là trung điểm của $CD$, $E$ là giao điểm của hai đường thẳng $AD$ và $BC.$
a) Trong mặt phẳng $(SBD)$ kẻ $DH \bot SB,{\rm{ (H}} \in {\rm{SB) (1)}}.$
+ Vì $BM = AD = \frac{1}{2}CD \Rightarrow $ Tam giác $BCD$ vuông tại $B$ hay $BC \bot BD{\rm{ (*)}}$. Mặt khác, vì $SD \bot (ABCD) \Rightarrow SD \bot BC{\rm{ (**)}}.$
Từ $(*)$ và $(**)$ ta có:
$BC \bot (SBD) \Rightarrow BC \bot DH{\rm{ (2)}}.$
Từ $(1)$ và $(2)$ suy ra: $DH \bot (SBC)$ hay $d(D,(SBC)) = DH.$
+ Xét tam giác vuông $SBD$ có: $\frac{1}{{D{H^2}}} = \frac{1}{{S{D^2}}} + \frac{1}{{B{D^2}}} = \frac{3}{{2{a^2}}}$ $ \Rightarrow DH = \frac{{2a\sqrt 3 }}{3}.$
Vậy $d(D,(SBC)) = \frac{{2a\sqrt 3 }}{3}.$
b) Ta có: $\frac{{d(A,(SBC))}}{{d(D,(SBC))}} = \frac{{AE}}{{DE}} = \frac{{AB}}{{CD}} = \frac{1}{2}$ $ \Rightarrow d(A,(SBC)) = \frac{1}{2}d(d,(SBC))$ $ = \frac{{a\sqrt 3 }}{3}.$
Vậy $d(A,(SBC)) = \frac{{a\sqrt 3 }}{3}.$

Ví dụ 7: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B$, $BA = 3a$, $BC = 4a$, $(SBC) \bot (ABC)$, $SB = 2a\sqrt 3 ,\widehat {SBC} = {30^0}$. Tính $d(B,(SAC))$.

+ Trong mặt phẳng $(SBC)$ kẻ $SM \bot BC{\rm{ (M}} \in {\rm{BC)}}$; trong mặt phẳng $(ABC)$ kẻ $MN \bot AC{\rm{ (N}} \in A{\rm{C)}}$; trong mặt phẳng $(SMN)$ kẻ $MH \bot SN{\rm{ (N}} \in SN{\rm{)}}$. Suy ra, $MH \bot (SAC)$ $ \Rightarrow d(M,(SAC)) = MH.$
+ Ta có: $SM = SB.\sin {30^0} = a\sqrt 3 .$
$BM = SB.\cos {30^0} = 3a$ $ \Rightarrow CM = a.$
$MN = \frac{{AB.CM}}{{AC}} = \frac{{3a}}{5}$. Xét tam giác vuông $SMN$ có: $\frac{1}{{M{H^2}}} = \frac{1}{{S{M^2}}} + \frac{1}{{M{N^2}}} = \frac{{28}}{{9{a^2}}}$ $ \Rightarrow MH = \frac{{3a}}{{\sqrt {28} }}$ $ \Rightarrow d(M,(SAC)) = \frac{{3a}}{{\sqrt {28} }}.$
+ Mặt khác, ta có:
$\frac{{d(B,(SAC))}}{{d(M,(SAC))}} = \frac{{BC}}{{MC}} = 4$ $ \Rightarrow d(B,(SAC))$ $ = 4.d(M,(SAC)) = \frac{{6a}}{{\sqrt 7 }}.$
Vậy $d(B,(SAC)) = \frac{{6a}}{{\sqrt 7 }}.$