Lý thuyết Ước chung và ước chung lớn nhất Toán 6 Cánh diều>

I. Ước chung

1. Định nghĩa

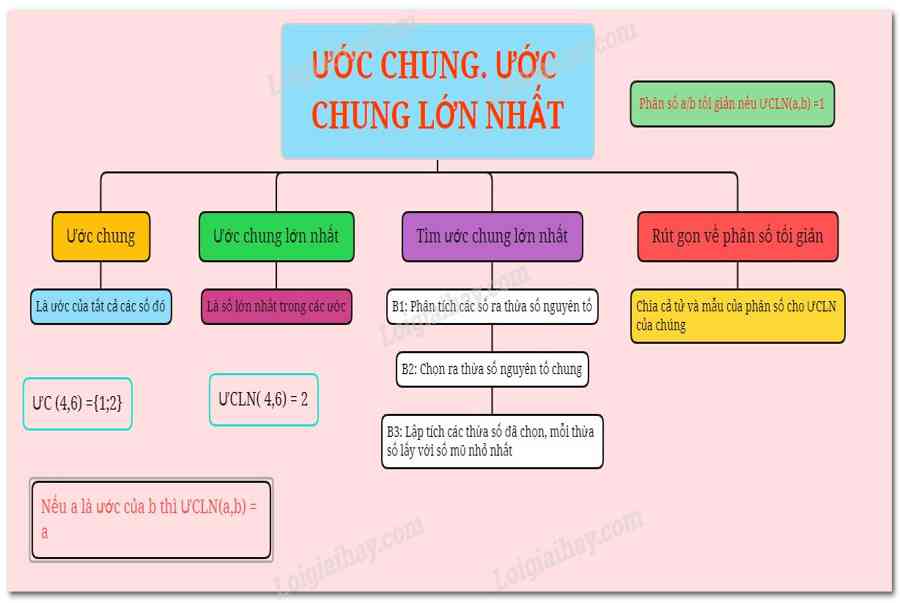
+ Ước chung của hai hay nhiều số là ước của tất cả các số đó.

2. Kí hiệu

+ ƯC\(\left( {a,b} \right)\) là tập hợp các ước chung của \(a\) và \(b\).

3. Cách tìm ước chung

a) Tìm ước chung của hai số a và b

Bước 1: Viết tập hợp các ước của a và của b: Ư(a), Ư(b)

Bước 2: Tìm những phần tử chung của Ư(a) và Ư(b).

Ví dụ: Ư\(\left( 8 \right) = \left\{ {1;2;4;8} \right\}\); Ư\(\left( {12} \right) = \left\{ {1;2;3;4;6;12} \right\}\)

Nên ƯC \ ( \ left ( { 8,12 } \ right ) = \ left \ { { 1 ; 2 ; 4 } \ right \ } \ )

b) Tìm ước chung của ba số a, b và c

Bước 1: Viết tập hợp các ước của a, của b và của c: Ư(a), Ư(b), Ư(c)

Bước 2: Tìm những phần tử chung của Ư(a), Ư(b) và Ư(c).

Nhận xét:

+) \(x \in \)ƯC\(\left( {a;b} \right)\) nếu \(a \vdots x\) và \(b \vdots x.\)

+ ) \ ( x \ in \ ) ƯC \ ( \ left ( { a, b, c } \ right ) \ ) nếu \ ( a \ vdots x \ ) ; \ ( b \ vdots x \ ) và \ ( c \ vdots x. \ )

Chú ý:

+ Giao của hai tập hợp là một tập hợp gồm những thành phần chung của hai tập hợp đó .
+ Kí hiệu : Giao của tập hợp A và tập hợp B là \ ( A \ cap B \ )

Ví dụ: Ư\(\left( 8 \right) \cap \) Ư\(\left( {12} \right) = \)ƯC\(\left( {8,12} \right)\).

II. Ước chung lớn nhất

1. Định nghĩa

Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.

Nếu ước chung lớn nhất của hai số a và b bằng 1 thì ta nói, a và b là hai số nguyên tố cùng nhau.

2. Kí hiệu

+) ƯCLN\(\left( {a,b} \right)\) là ước chung lớn nhất của \(a\) và \(b\).

+) ƯC\(\left( {a,b} \right)\) là tập hợp còn ƯCLN\(\left( {a,b} \right)\) là một số.

3. Các cách tìm ước chung lớn nhất bằng định nghĩa

a) Cách tìm ƯCLN  trong trường hợp đặc biệt

+) Trong các số cần tìm ƯCLN có số nhỏ nhất là ước của những số còn lại thì số đó là ƯCLN cần tìm:

Nếu \(a \vdots b\) thì ƯCLN \(\left( {a,b} \right) = b\)

+ ) Số 1 chỉ có 1 ước là 1 nên với mọi số tự nhiên a và b ta có :

ƯCLN\(\left( {a,1} \right)\) =1 và ƯCLN\(\left( {a,b,1} \right)\)=1

b) Cách tìm ƯCLN  của hai số a và b bằng định nghĩa

Bước 1. Tìm tập hợp các ước chung của hai số a và b: ƯC\(\left( {a,b} \right)\)

Bước 2. Tìm số lớn nhất trong các ước chung vừa tìm được: ƯCLN\(\left( {a,b} \right)\)

Ví dụ : Tìm ƯCLN (18, 30)

Ta có :Ư ( 18 ) = \ ( \ left \ { { 1 ; 2 ; 3 ; 6 ; 9 ; 18 } \ right \ } \ )Ư ( 30 ) = \ ( \ left \ { { 1 ; 2 ; 3 ; 5 ; 6 ; 10 ; 15 ; 30 } \ right \ } \ )ƯC ( 18,30 ) = { 1 ; 2 ; 3 ; 6 }Số lớn nhất trong những số 1, 2, 3, 6 là số 6 .Vậy ƯCLN ( 18, 30 ) = 6

III. Tìm ước chung lớn nhất bằng cách phân tích các số tự nhiên ra thừa số nguyên tố

1. Cách tìm ước chung lớn nhất –ƯCLN

Muốn tìm ƯCLN của của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau :

Bước 1 : Phân tích mỗi số ra thừa số nguyên tố.

Bước 2 : Chọn ra các thừa số nguyên tố chung.

Bước 3 : Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.

Ví dụ : Tìm ƯCLN (18 ; 30)

Ta có :

Bước 1 : phân tích các số ra thừa số nguyên tố.

18 = 2.3230 = 2.3.5

Bước 2 : Thừa số nguyên tố chung là \(2\) và \(3\)

Bước 3 : ƯCLN\(\left( {18, 30} \right) = 2.3 = 6\)

Chú ý:  

+ Nếu các số đã cho không có thừa số nguyên tố chung thì ƯCLN của chúng bằng 1.

+ Hai hay nhiều số có ƯCLN bằng 1 gọi là các số nguyên tố cùng nhau.

2. Cách tìm ƯC thông qua ƯCLN

Để tìm ước chung của những số đã cho, ta có tể tìm những ước của ƯCLN của những số đó .

Ví dụ: ƯCLN\(\left( {18,30} \right) = 2.3 = 6\)

Từ đó ƯC \ ( \ left ( { 18,30 } \ right ) = \ ) Ư \ ( \ left ( 6 \ right ) = \ left \ { { 1 ; 2 ; 3 ; 6 } \ right \ } \ )

IV. Ứng dụng trong rút gọn về số tối giản

Rút gọn phân số: Chia cả tử và mẫu cho ước chung khác 1 (nếu có) của chúng.

Phân số tối giản: \(\dfrac{a}{b}\) là phân số tối giản nếu ƯCLN\(\left( {a,b} \right) = 1\)

Đưa một phân số chưa tối giản về phân số tối giản: Chia cả tử và mẫu cho ƯCLN\(\left( {a,b} \right)\).

Ví dụ: Phân số \(\dfrac{9}{{24}}\) tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản.

Ta có : ƯCLN \ ( \ left ( { 9,24 } \ right ) = 3 \ ) khác 1 nên \ ( \ dfrac { 9 } { { 24 } } \ ) chưa tối giản .Ta có : \ ( \ dfrac { 9 } { { 24 } } = \ dfrac { { 9 : 3 } } { { 24 : 3 } } = \ dfrac { 3 } { 8 } \ ). Ta được \ ( \ dfrac { 3 } { 8 } \ ) là phân số tối giản .

CÁC DẠNG TOÁN VỀ ƯỚC CHUNG. ƯỚC CHUNG LỚN NHẤT

I. Nhận biết và viết tập hợp các ước chung của hai hay nhiều số

Phương pháp:

Để nhận ra 1 số ít là ước chung của hai số, ta kiểm tra xem hai số đó có chia hết cho số này hay không .

Để viết tập hợp những ước chung của hai hay nhiều số, ta viết tập hợp những ước của mỗi số rồi tìm giao của những tập hợp đó .

II. Bài toán đưa về việc tìm ước chung, ƯCLN của hai hay nhiều số

Phương pháp:

Phân tích bài toán để đưa về việc tìm ước chung, ƯCLN của hai hay nhiều số .

Ví dụ:

Một bác thợ mộc muốn làm kệ để đồ từ hai tấm gỗ dài 18 dm và 30 dm. Bác muốn cắt hai tấm gỗ này thành những thanh gỗ có cùng độ dài mà không để thừa mẩu gỗ nào. Em hãy giúp bác thợ mộc tìm độ dài lớn nhất hoàn toàn có thể của mỗi thanh gỗ được cắt .GiảiĐộ dài lớn nhất những thanh gỗ được cắt chính là ƯCLN của 18 và 30 .Ta có : ƯCLN ( 18, 30 ) = 6Vậy độ dài lớn nhất hoàn toàn có thể của những thanh gỗ được cắt là 6 dm .

III. Tìm các ước chung của hai hay nhiều số thỏa mãn điều kiện cho trước

Phương pháp:

+ Tìm ƯCLN của hai hay nhiều số cho trước.

+ Tìm những ước của ƯCLN .+ Chọn trong số đó những ước hoặc những bội thỏa mãn nhu cầu điều kiện kèm theo đã cho .