Giải Sách Bài Tập Toán 9 Bài 2: Căn Thức Bậc Hai Và Hằng Đẳng Thức

Xem toàn bộ tài liệu Lớp 9: tại đây

Xem thêm các sách tham khảo liên quan:

Sách Giải Sách Bài Tập Toán 9 Bài 2 : Căn thức bậc hai và hằng đẳng thức giúp bạn giải những bài tập trong sách bài tập toán, học tốt toán 9 sẽ giúp bạn rèn luyện năng lực suy luận hài hòa và hợp lý và hợp logic, hình thành năng lực vận dụng kết thức toán học vào đời sống và vào những môn học khác :

Bài 12 trang 7 Sách bài tập Toán 9 Tập 1: Tìm x để căn thức sau có nghĩa:

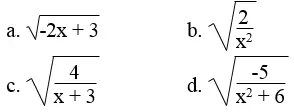
Lời giải:

a. Ta có: 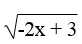có nghĩa khi và chỉ khi:

– 2 x + 3 ≥ 0 ⇒ – 2 x ≥ – 3 ⇒ x ≤ 3/2

b. Ta có: có nghĩa khi và chỉ khi:

2 / x2 ≥ 0 ⇒ x2 > 0 ⇒ x ≠ 0
c. Ta có :
có nghĩa khi và chỉ khi:
có nghĩa khi và chỉ khi :

> 0 ⇒ x + 3 > 0 ⇒ x > -3

d. Ta có : x2 ≥ 0 với mọi x nên x2 + 6 > 0 với mọi x

Suy ra < 0 với mọi x

Vậy không có giá trị nào của x để
có nghĩa.

Bài 13 trang 7 Sách bài tập Toán 9 Tập 1: Rút gọn rồi tính:

có nghĩa .

Lời giải:

Bài 14 trang 7 Sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức sau:

Lời giải:

Bài 15 trang 7 Sách bài tập Toán 9 Tập 1: Chứng minh:

Lời giải:

a. Ta có :
VT = 9 + 4 √ 5 = 4 + 2.2 √ 5 + 5 = 22 + 2.2 √ 5 + ( √ 5 ) 2 = ( 2 + √ 5 ) 2
Vế trái bằng vế phải nên đẳng thức được chứng tỏ .
b. Ta có :

Vế trái bằng vế phải nên đẳng thức được chứng tỏ .
c. Ta có :
VT = ( 4 – √ 7 ) 2 = 42 – 2.4. √ 7 + ( √ 7 ) 2 = 16 – 8 √ 7 + 7 = 23 – 8 √ 7
Vế trái bằng vế phải nên đẳng thức được chứng tỏ .
d. Ta có :

Vế trái bằng vế phải nên đẳng thức được chứng tỏ .

Bài 16 trang 7 Sách bài tập Toán 9 Tập 1: Biểu thức sau đây xác định với giá trị nào của x?

Lời giải:

Bài 17 trang 8 Sách bài tập Toán 9 Tập 1: Tìm x, biết:

Lời giải:

= 2 x + 1 ⇔ | 3 x | = 2 x + 1 ( 1 )
* Trường hợp 1 : 3 x ≥ 0 ⇔ x ≥ 0 ⇒ | 3 x | = 3 x
Suy ra : 3 x = 2 x + 1 ⇔ 3 x – 2 x = 1 ⇔ x = 1
Giá trị x = 1 là nghiệm của phương trình ( 1 ) .
* Trường hợp 2 : 3 x < 0 ⇔ x < 0 ⇒ | 3 x | = – 3 x
Suy ra : – 3 x = 2 x + 1 ⇔ – 3 x – 2 x = 1 ⇔ – 5 x = 1 ⇔ x = – 1/5
Giá trị x = – 1/5 thỏa mãn nhu cầu điều kiện kèm theo x < 0
Vậy x = – 1/5 là nghiệm của phương trình ( 1 ) .
Vậy x = 1 và x = – 1/5

⇔ | x + 3 | = 3 x – 1 ( 2 )
* Trường hợp 1 : x + 3 ≥ 0 ⇔ x ≥ – 3 ⇒ | x + 3 | = x + 3
Suy ra : x + 3 = 3 x – 1 ⇔ x – 3 x = – 1 – 3 ⇔ – 2 x = – 4 ⇔ x = 2
Giá trị x = 2 thỏa mãn nhu cầu điều kiện kèm theo x ≥ – 3 .
Vậy x = 2 là nghiệm của phương trình ( 2 ) .
* Trường hợp 2 : x + 3 < 0 ⇔ x < – 3 ⇒ | x + 3 | = – x – 3
Suy ra : – x – 3 = 3 x – 1 ⇔ – x – 3 x = – 1 + 3 ⇔ – 4 x = 2 ⇔ x = – 0.5
Giá trị x = – 0,5 không thỏa mãn nhu cầu điều kiện kèm theo x < – 3 : loại
Vậy x = 2

= 5 ⇔ |1 – 2x| = 5 (3)

* Trường hơp 1 : 1 – 2 x ≥ 0 ⇔ 2 x ≤ 1 ⇔ x ≤ 50% ⇒ | 1 – 2 x | = 1 – 2 x
Suy ra : 1 – 2 x = 5 ⇔ – 2 x = 5 – 1 ⇔ x = – 2
Giá trị x = – 2 thỏa mãn nhu cầu điều kiện kèm theo x ≤ 1/2
Vậy x = – 2 là nghiệm của phương trình ( 3 ) .
* Trường hợp 2 : 1 – 2 x < 0 ⇔ 2 x > 1 ⇔ x > 12 ⇒ | 1 – 2 x | = 2 x – 1
Suy ra : 2 x – 1 = 5 ⇔ 2 x = 5 + 1 ⇔ x = 3
Giá trị x = 3 thỏa mãn nhu cầu điều kiện kèm theo x > 50%
Vậy x = 3 là nghiệm của phương trình ( 3 ) .
Vậy x = – 2 và x = 3 .

⇔ | x2 | = 7 ⇔ x2 = 7
Vậy x = √ 7 và x = – √ 7 .

Bài 18 trang 8 Sách bài tập Toán 9 Tập 1: Phân tích thành nhân tử:

a. x2 – 7 b. x2 – 2 √ 2 x + 2 c. x2 + 2 √ 13 x + 13

Lời giải:

a. Ta có : x2 – 7 = x2 – ( √ 7 ) 2 = ( x + √ 7 ) ( x – √ 7 )
b. Ta có : x2 – 2 √ 2 x + 2 = x2 – 2. x. √ 2 + ( √ 2 ) 2 = ( x – √ 2 ) 2
c. Ta có : x2 + 2 √ 13 x + 13 = x2 + 2. x. √ 13 + ( √ 13 ) 2 = ( x + √ 13 ) 2

Bài 19 trang 8 Sách bài tập Toán 9 Tập 1: Rút gọn các phân thức:

Lời giải:

Bài 20 trang 8 Sách bài tập Toán 9 Tập 1: So sánh(không dùng bảng số hay máy tính bỏ túi):

a. 6 + 2 √ 2 và 9 b. √ 2 + √ 3 và 3
c. 9 + 4 √ 5 và 16 d. √ 11 – √ 3 và 2

Lời giải:

a. 6 + 2 √ 2 và 9
Ta có : 9 = 6 + 3
So sánh : 2 √ 2 và 3 vì 2 √ 2 > 0 và 3 > 0
Ta có : ( 2 √ 2 ) 2 = 22. ( √ 2 ) 2 = 4.2 = 8
32 = 9
Vì 8 < 9 nên : ( 2 √ 2 ) 2 < 32
Vậy 6 + 2 √ 2 < 9 . b. √ 2 + √ 3 và 3 Ta có : ( √ 2 + √ 3 ) 2 = ( √ 2 ) 2. ( √ 3 ) 2 = 2.3 = 6 22 = 4 Vì 6 > 4 nên ( √ 2. √ 3 ) 2 > 22
Suy ra : √ 2. √ 3 > 2 ⇒ 2. √ 2. √ 3 > 2.2 ⇒ 5 + 2. √ 2. √ 3 > 4 + 5
⇒ 5 + 2. √ 2. √ 3 > 9 ⇒ ( √ 2 + √ 3 ) 2 > 9 ⇒ ( √ 2 + √ 3 ) 2 > 32
Vậy √ 2 + √ 3 > 3
c. 9 + 4 √ 5 và 16
So sánh 4 √ 5 và 5
Ta có : 16 > 5 ⇒ √ 16 > √ 5 ⇒ 4 > √ 5
Vì √ 5 > 0 nên 4. √ 5 > √ 5. √ 5 ⇒ 4 √ 5 > 5 ⇒ 9 + 4 √ 5 > 5 + 9
Vậy 9 + 4 √ 5 > 16
d. √ 11 – √ 3 và 2
Vì √ 11 > √ 3 nên √ 11 – √ 3 > 0
Ta có : ( √ 11 – √ 3 ) 2 = 11 – 2 √ 11. √ 3 + 3 = 14 – 2 √ 11. √ 3
22 = 4 = 14 – 10
So sánh 10 và 2 √ 11. √ 3 hay so sánh giữa 5 và √ 11. √ 3
Ta có : 52 = 25
( √ 11. √ 3 ) 2 = ( √ 11 ) 2. ( √ 3 ) 2 = 11.3 = 33
Vì 25 < 33 nên 52 < ( √ 11. √ 3 ) 2
Suy ra : 5 < ( √ 11. √ 3 ) 2 Suy ra : 14 – 10 > 14 – 2 √ 11. √ 3 ⇒ ( √ 11 – √ 3 ) 2 < 22
Vậy √ 11 – √ 3 < 2

Bài 21 trang 8 Sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức:

Lời giải:

Bài 22 trang 8 Sách bài tập Toán 9 Tập 1: Với n là số tự nhiên, chứng minh đẳng thức:

Viết đẳng thức trên khi n là 1, 2, 3, 4, 5, 6, 7

Lời giải:

Bài 2 trang 8 Sách bài tập Toán 9 Tập 1: Đẳng thức nào đúng nếu x là số âm

A. √ ( 9×2 ) = 9 x ; B. √ ( 9×2 ) = 3 x ;
C. √ ( 9×2 ) = – 9 x ; D. √ ( 9×2 ) = – 3 x .

Hãy chọn đáp án đúng.

Lời giải:

Chọn đáp án D