Tính chất đường trung trực của một đoạn thẳng, một tam giác

Ngày nay, việc học toán ngày khó số lượng kiến thức cần phải tiếp thu rất là nhiều, vì vậy rất nhiều học sinh cảm thấy chán nản vì không thể nhớ hết được. Hiểu được sự khó khăn trong việc ghi nhớ môn toán, hôm nay Toppy sẽ gửi đến cho các bạn một số tính chất đường trung trực và dạng bài thường gặp để cho bạn có thể dễ dàng học hơn. 

Tính chất đường trung trực của một đoạn thẳng

Định nghĩa : Đường trung trực của một đoạn thẳng là đường thẳng đi trung điểm và vuông góc với đoạn thẳng ấy .
D là đường thẳng trung trực của đoạn thẳng AB

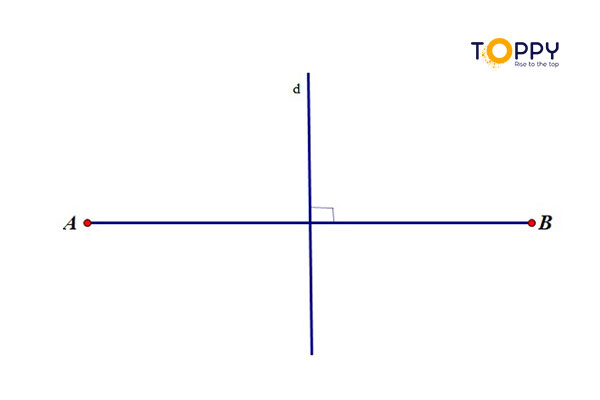
Định lý 1: Điểm nằm trên đường trung trực thì cách đều hai mút của đoạn thẳng đó.

Ví dụ : d là đường trung trực của đoạn thẳng AB, M là một điểm nằm trên d => MA = MB

Định lý 2: Điểm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Ví dụ : MA = MB thì ta hoàn toàn có thể xác lập rằng M nằm trên đường trực của đoạn thẳng AB

Tính chất đường trung trực của một tam giác

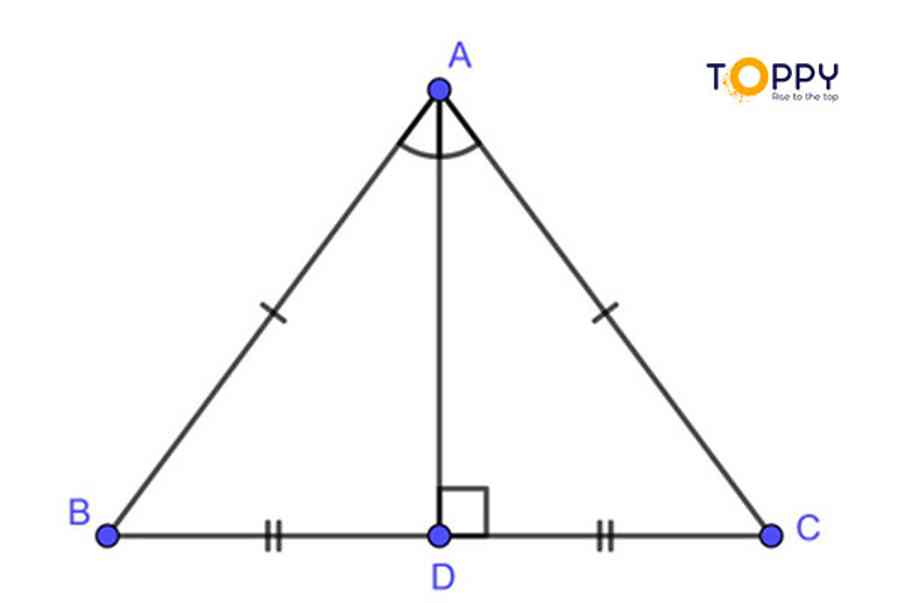
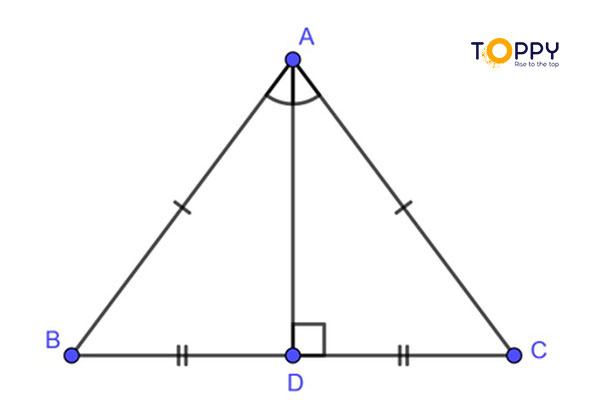
Định lý 3 : Trong một tam giác cân đường trung trực của một cạnh đồng thời cũng sẽ là đường trung tuyến so với cạnh đó .
Ví dụ : AM là đường trung trực của của cạnh BC đồng thời AM cũng là cũng là đường trung tuyến của cạnh BC .
Định lý 4 : Nếu ba đường thẳng trung trực của một tam giác cùng đi qua một điểm thì điểm này sẽ cách đều 3 đỉnh của tam giác đó .
Ví dụ : Cho tam giác ABC, 3 đường trung trực của tam giác đều giao tại một điểm O
=> OA = OB = OC => Điểm O chính là tâm đường tròn ngoại tiếp của tam giác ABC

>> Xem thêm:

Các dạng bài toán thường gặp

• Dạng 1 : Chứng minh đường trung trực của một đoạn thẳng

Để có thể chứng minh d là đường trung trực của đoạn thẳng AB, ta chỉ cần chứng minh hai điểm A và chứa các điểm cách đều d hoặc sử dụng định nghĩa về tính chất đường trung trực để xác định.

• Dạng 2 : Chứng minh hai đoạn thẳng bằng nhau

Sử dụng định lý sổ 1 để tìm ra cách chứng tỏ nhanh nhất .
Định lý 3 : Điểm nằm trên đường trung trực thì cách đều hai mút của đoạn thẳng đó .

• Dạng 3 : Bài tập về tính giá trị nhỏ nhất

Áp dụng tính chất đường trung trực để có thể thay đổi độ dài của một đoạn thẳng thành một con số chiều dài của một đoạn thẳng khác bằng nó. Sau đó sử dụng bn  bất đẳng thức của tam giác để tìm được giá trị nhỏ nhất.

• Dạng 4 : Xác định tâm đường tròn ngoại tiếp tam giác

Sử dụng định lý sổ 4 để tìm ra cách chứng tỏ nhanh nhất .
Định lý 4 : Nếu ba đường thẳng trung trực của một tam giác cùng đi qua một điểm thì điểm này sẽ cách đều 3 đỉnh của tam giác đó .

• Dạng 5 : Bài toán tương quan đến đường trung trực của một tam giác cân

Để làm được dạng bài tập này, bạn nên quan tâm rằng trong một cân đường trung trực cũng chính là đường trung tuyến, đường phân giác ứng với cạnh đáy .

• Dạng 6: Bài toán liên quan đến đường trung trực của một tam giác vuông

  Xem thêm: Những Câu nói Hay về Anh Em Xã Hội cực chất, đáng suy ngẫm – Chuyên Tour Trekking – Camping – Team Building | http://139.180.218.5

Bạn chỉ cần nhớ, trong một tam giác vuông giao điểm đường trung trực là trung điểm của cạnh huyền .

Bài tập vận dụng

Câu 1 : Gọi O là điểm của ba đường trung trực của tam giác ABC. Khi đó O là :

1. Điểm cách đều 3 cạnh của tam giác ABC
2. Điểm cách đều 3 đỉnh của tam giác ABC
3. Tâm đường đường tròn ngoại tiếp tam giác ABC
4. Đáp án B và C đúng

Câu 2 : Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì ?

1. Tam giác vuông
2. Tam giác cân
3. Tam giác đều
4. Tam giác vuông cân

Câu 3 : Trên đường trung trực của đoạn thẳng AB lấy điểm M. Hạ MH ⊥ AB. Trên đoạn MH lấy điểm P., gọi E là giao điểm của MB với AP. Gọi F là giao điểm của BP với MA

1. Chứng minh MH là phân giác của góc AMB
2. Chứng minh MH là trung trực của đoạn thẳng EF
3. Chứng minh AF = BE

Câu 4 : Cho tam giác △ ABC cân tại A. Hai đường trung tuyến CN và BM cắt nhau tại I. Hai tia phân giác trong của B và C cắt nhau tại O. Hai đường trung trực của 2 cạnh AB, AC cắt nhau tại K .

1. Chứng minh rằng : BM = CN .
2. Chứng minh rằng OB = OC
3. Chứng minh 4 điểm A, O, I, K thẳng hàng .

Câu 5 : Cho góc xOy = 50 º, điểm A nằm trong góc xOy. Vẽ điểm M sao cho Ox là trung trực của AN, vẽ điểm M sao cho Oy là trung trực của AM .

1. Chứng minh rằng OM = ON

   Xem thêm: Stt bầu trời – Những câu nói, cap hay về bầu trời

2. Tính số đo MON

Lời kết

Trên đây là một số kiến thức cơ bản về tính chất đường trung trực của đoạn thẳng, một tam giác mà Toppy muốn gửi đến cho các bạn học sinh. Hy vọng bài viết bổ ích này sẽ giúp các bạn dễ dàng tiếp thu kiến thức về tính chất đường trung trực hơn. Nếu các bạn còn muốn tìm hiểu thêm các công thức tính toán khác thì hay truy cập ngay vào website: http://139.180.218.5/ của chúng tôi để tìm hiểu nhé!

Xem ngay: