Công thức tính chu vi và diện tích lục giác đều chuẩn SKG

1.8 / 5 – ( 6 bầu chọn )

Các phép tính trong toán học luôn là những vấn đề nan giải cho chúng ta khi còn ngồi trên ghế nhà trường. Việc phải ghi nhớ một công thức nào đó không phải là một điều dễ dàng. Vì thế bài viết dưới đây sẽ giúp cho bạn ôn tập lại những kiến thức liên quan đến hình học không gian đó là công thức tính chu vi và diện tích lục giác đều. Mọi người đừng vội vã bỏ qua nhé.

Hình lục giác là gì?

Hình học trong khoảng trống có rất nhiều mô hình như hình tứ giác, hình tam giác, hình tròn trụ, hình vuông vắn, hình chữ nhật, hình lục giác, … Vậy hình lục giác là gì ?

Khi chúng ta biết phân định được hình lục giác thì mới có thể áp dụng được công thức tính chu vi và diện tích lục giác đều chuẩn nhất.

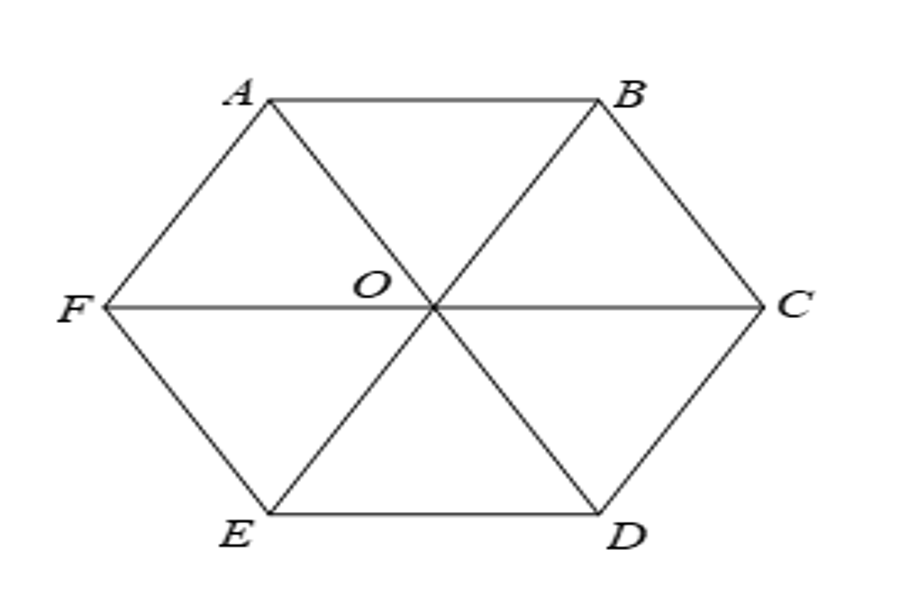
Hình lục giác
Một hình lục giác hoặc còn được gọi là hình sáu cạnh : chúng là một đa giác, nằm trong một hình thể của hình học phẳng, gồm có có tổng thể sáu góc và sáu cạnh .
Diện tích của lục giác thường được hình thành như sau : muốn tính được diện tích của một hình lục giác thường thì ta hoàn toàn có thể chia được hình lục giác ra thành bốn hình tam giác, sau đó tính tổng hết tổng thể diện tích của những hình tam giác đó và đi tìm ra hiệu quả diện tích của hình lục giác .

Lục giác đều là hình gì?

Khái niệm về hình lục giác đều:

Sau khi đã phân tích được hình lục giác là gì? Thì ta sẽ đi tìm hiểu về lục giác đều, vì có lục giác đều ta mới có được công thức tính chu vi và diện tích lục giác đều.

Hình lục giác đều
Nếu sáu cạnh mà có số chiều dài bằng với nhau, được gọi là một hình lục giác với sáu cạnh đều nhau. Chỉ khi tổng thể những cạnh góc đã có cùng một size, và những cạnh bằng nhau thì mới hoàn toàn có thể gọi là hình lục giác đều .
Trong khi đó một hình khối gồm có hai đáy hình lục giác sẽ được gọi là lục lăng .

Đặc điểm của hình lục giác đều :

Các cạnh trong hình lục giác đều bằng nhau và những góc ở đỉnh cũng bằng nhau .
Tâm nằm ở đường tròn ngoại hay nội tiếp với hình chính là tâm đối xứng quay quanh hoặc tỏa tròn .

Tổng số đo ở mỗi góc nằm tại đỉnh là : 

,mà n chín là số cạnh của hình đa giác đều. Như vậy độ lớn của các góc ở đỉnh sẽ là:

Gọi R lớn và r nhỏ là nửa đường kính nằm trong đường tròn ngoại hay nội tiếp của một hình đa giác đều, đồng thời thì sẽ gọi cạnh của hình đa giác đều là a và ta có được :

Những cạnh của chúng đều dài đúng bằng với nửa đường kính của đường tròn ngoại tiếp .
Nếu như nối tâm với đường tròn ngoại hoặc nội tiếp với mọi đỉnh của hình lục giác thì tất cả chúng ta sẽ có đủ sáu tam giác đều .

Tham khảo thêm :

Công thức chu vi và diện tích lục giác đều chuẩn nhất hiện nay là gì?

Công thức tính chu vi lục giác đều là gì?

Các khái niệm về lục giác đều khi đã được phân định rõ ràng thì ta sẽ dễ dàng áp dụng những công thức tính toán liên quan như tính chu vi lục giác đều và tính diện tích lục giác đều.

Về mặt cơ bản thì phép tính chu vi của lục giác đều khá đơn giản, không quá khó khăn đối với chúng ta.

Công thức để tính chu vi của hình lục giác đều :

P = a x 6

Chú thích :

• P. chính là kí hiệu bộc lộ cho chu vi của hình lục giác đều
• a chính là chiều dài của những cạnh trong hình lục giác đều .

Ngoài ra còn có công thức để tính nửa đường kính cho đường tròn ngoại tiếp của một hình lục giác đều :
Công thức tính nửa đường kính với đường tròn ngoại tiếp của một hình lục giác đều :

R = a

Chú thích :

• R chính là nửa đường kính trong đường tròn ngoại tiếp của hình lục giác đều
• a chính là độ dài của những cạnh trong hình lục giác đều

Công thức tính diện tích hình lục giác đều là gì?

Mỗi hình đều có công thức tính diện tích, chu vi và thể tích riêng. Vậy công thức để tính diện tích lục giác đều là gì?

Trong hình lục giác đều kể cả chu vi hay diện tích đều không quá khó để đi tìm. Chỉ cần tất cả chúng ta ghi nhớ thật kĩ phép tính bằng cách làm thật nhiều bài tập tương quan đến hình học lục giác .

Để tính được diện tích lục giác đều thì ta sẽ sử dụng công thức như sau:

Công thức tính diện tích lục giác đều
Chú thích :

• S chính là kí hiệu của diện tích hình lục giác đều
• a chính là độ dài của những cạnh hình lục giác đều

Thông qua cả hai công thức giám sát tất cả chúng ta hoàn toàn có thể thấy hình học không quá khó như bạn nghĩ. Nếu như tất cả chúng ta hoàn toàn có thể hiểu chúng và nghiên cứu và phân tích, vận dụng đúng phép tính thì mọi thứ sẽ trở nên đơn thuần .
Lưu ý rằng khi làm toán hình, những bạn phải tập vẽ hình giống như học toán số hay hóa học, vật lý phải ghi tóm tắt để giải bài một cách thuận tiện hơn. Vẽ hình sẽ giúp ta nghiên cứu và phân tích rõ ràng những yếu tố có trong bài toán .

Ứng dụng của lục giác đều có trong đời sống thực tế là gì?

Nếu như các bạn nghĩ hình học không gian, công thức tính chu vi và diện tích lục giác đều chỉ áp dụng trong sách vở thì đó là một suy nghĩ sai lầm. Các phép tính có ở sách giáo khoa đều được áp dụng vào cuộc sống thực tế, tùy thuộc vào mỗi ngành nghề mà ta sẽ có cách áp dụng khác nhau.

Những lỗ tổ ong mật đều là hình lục giác đều:

Hình lục giác đều xuất hiện ở khắp mọi nơi, từ môi trường thiên nhiên cho đến môi trường nhân tạo.

Theo như những bạn đã biết, con ong còn được coi là những nhà kiến trúc sư đa tài ở trong quốc tế loài vật. Nếu như có thời cơ để quan sát tổ ong thì bạn sẽ nhìn thấy những cái lỗ ở trên tổ đều có hình lục giác đều gồm có sáu góc và sáu cạnh bằng với nhau nằm sát kề nhau .

Hình lục giác đều được ứng dụng trong đời sống
Vốn dĩ con ong lựa chọn cách kiến thiết xây dựng tổ cho mình như vậy cũng chính vì chu vi lục giác là nhỏ nhất trong số tổng thể những hình tam giác hoặc hình vuông vắn. Ngoài ra hơn nữa cấu trúc của lỗ tổ có hình lục giác, sức chứa lên tới tối đa, đồng thời có độ bền lớn .

Nước Pháp được mệnh danh là đất nước hình lục giác:

Chắc hẳn rằng khi nhắc đến đất nước Pháp hay còn được gọi là Cộng hòa Pháp, bạn sẽ liền nghĩ ngay đến kiến trúc vĩ đại tháp Ép-phen, với các cánh đồng chứa đầy hoa oải hương tím ngắt,… 

Nhưng mà bạn cũng sẽ khá giật mình khi biết được khoanh vùng phạm vi của chủ quyền lãnh thổ nước Pháp xuất hiện trên map theo hình dáng lục giác gồm có sáu cạnh rất mê hoặc. Bởi vì vậy mà quốc gia Pháp còn hay được gọi với cái tên quốc gia hình lục lăng .

Hình lục giác là dạng hình khối vô cùng phổ biến nằm trong xây dựng lăng mộ:

Chắc hẳn đã có đôi lúc bạn vô tình hay bắt gặp thấy những ngôi mộ được xây dựng bằng đá theo hình dạng lục giác đều, vậy tại sao người ta lại chọn khối hình này để chọn lựa xây dựng lăng mộ? 

Với lí do khá đơn thuần đó là khối lục giác được chọn chúng đều có ý nghĩa trong tự nhiên, chúng đại diện thay mặt và hình tượng cho sự tuyệt vời đồng thời là sự đẹp tươi của tự nhiên .
Hơn thế nữa về cách xây lăng mộ theo hình lục giác sẽ giúp cho ta tiết kiệm chi phí được những vật tư, tiết kiệm ngân sách và chi phí ngân sách cho khu công trình mà còn hoàn toàn có thể giữ được độ lâu bền, cạnh bên đó còn giữ được những ý nghĩa về mặt tử vi & phong thủy .

Công thức tính chu vi và diện tích lục giác đều rất quan trọng trong xây dựng, chúng góp phần tạo nên những bản thiết kế và các công trình kiến trúc hùng vĩ.