Nội dung chính
Cách tính Thể tích khối lăng trụ đứng- Bài tập có đáp án
Công thức tính thể tích khối lăng trụ:
USD V = S.h $
Trong đó : S là diện tích quy hoạnh đáy và h là chiều cao của khối lăng trụ .
Chú ý: Lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.
Bài tập trắc nghiệm thể tích khối lăng trụ có đáp án chi tiết
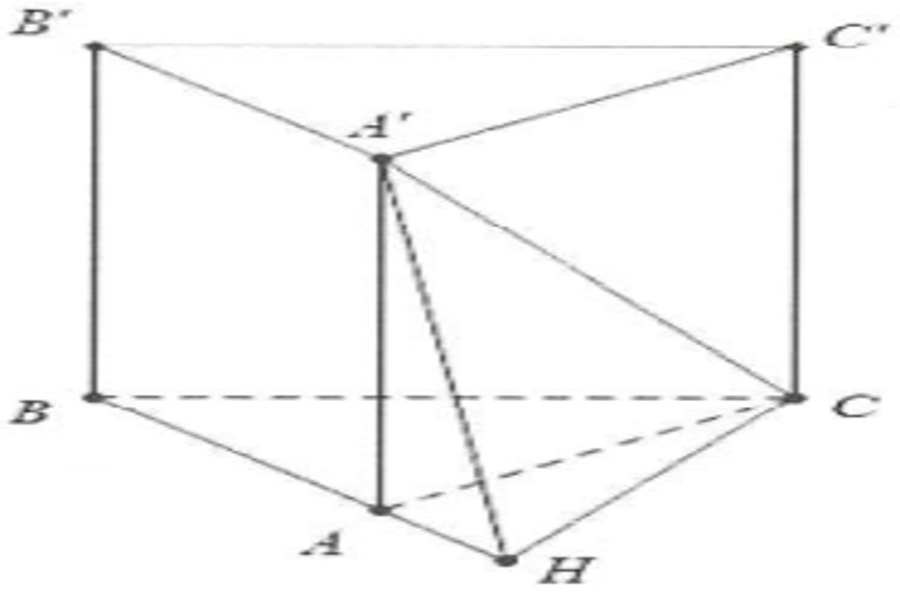
| Bài tập 1: Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}’$có đáy là tam giác dều cạnh a. Biết mặt phẳng (A’BC) tạo với đáy một góc 60°. Thể tích khối lăng trụ đã cho là:
A. $\frac{2{{a}^{3}}\sqrt{3}}{4}$ B. $\frac{{{a}^{3}}\sqrt{3}}{8}$ C. $\frac{3{{a}^{3}}\sqrt{3}}{8}$ D. $\frac{3{{a}^{3}}\sqrt{3}}{4}$ |
Lời giải chi tiết
Diện tích đáy cùa lăng trụ là USD { { S } _ { ABC } } = \ frac { { { a } ^ { 2 } } \ sqrt { 3 } } { 4 }. $
Dựng $ AH \ bot BC, USD có $ BC \ bot A { A } ‘ \ Rightarrow BC \ bot ( { A } ‘ HA ) USD
Do đó : $ \ widehat { \ left ( \ left ( { A } ‘ BC \ right ) ; \ left ( ABC \ right ) \ right ) } = \ widehat { { A } ‘ HA \ text { } } = 60 { } ^ \ circ USD
Ta có : USD AH = \ frac { a \ sqrt { 3 } } { 2 } \ Rightarrow { A } ‘ H = AH \ tan 60 { } ^ \ circ = \ frac { 3 a } { 2 }. $
Thể tích khối lăng trụ là: $V={{S}_{ABC}}.A{A}’=\frac{3{{a}^{3}}\sqrt{3}}{8}.$ Chọn C
| Bài tập 2: Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}’$ có đáy là tam giác đều cạnh a. Đường thẳng ${A}’C$ tạo với mặt phẳng $(BC{C}'{B}’)$ một góc $30{}^\circ $. Thể tích khối lăng trụ đã cho là
A. $\frac{{{a}^{3}}\sqrt{15}}{5}$ B. $\frac{{{a}^{3}}\sqrt{6}}{8}$ C. $\frac{{{a}^{3}}\sqrt{15}}{8}$ D. $\frac{{{a}^{3}}\sqrt{6}}{4}$ |
Lời giải chi tiết
Dựng $ { A } ‘ H \ bot { B } ‘ { C } ‘ \ Rightarrow $ H là trung điểm của USD { B } ‘ { C } ‘ $ .
Mặt khác USD { A } ‘ H \ bot B { B } ‘ \ Rightarrow { A } ‘ H \ bot ( BC { C } ‘ { B } ‘ ) USD .
Khi đó $ \ widehat { ( { A } ‘ C ; ( BC { C } ‘ { B } ‘ ) } ) = \ widehat { { A } ‘ CH } = 30 { } ^ \ circ USD
Ta có : USD { A } ‘ C \ sin 30 { } ^ \ circ – { A } ‘ H – \ frac { a \ sqrt { 3 } } { 2 } \ Rightarrow { A } ‘ C = a \ sqrt { 3 } $
Suy ra $ A { A } ‘ = \ sqrt { { A } ‘ { { C } ^ { 2 } } – A { { C } ^ { 2 } } } = a \ sqrt { 2 }. $
Thể tích khối lăng trụ là : USD V = { { S } _ { ABC } }. A { A } ‘ = \ frac { { { a } ^ { 2 } } \ sqrt { 3 } } { 4 }. a \ sqrt { 2 } = \ frac { { { a } ^ { 3 } } \ sqrt { 6 } } { 4 } $
Chọn D.
| Bài tập 3: Cho hình lăng trụ đứng$ABC.{A}'{B}'{C}’$có đáy là tam giác vuông cân tại A có $AB=AC=a$. Biết diện tích tam giác ${A}’BC$ bằng $\frac{{{a}^{2}}\sqrt{3}}{2}$. Thể tích khối lăng trụ đã cho là
A. $2{{a}^{3}}$ B. ${{a}^{3}}$ C. $\text{3}{{a}^{3}}$ D. $\frac{{{a}^{3}}}{2}$ |
Lời giải chi tiết
Diện tích đáy của lăng trụ là USD { { S } _ { ABC } } = \ frac { { { a } ^ { 2 } } } { 2 }. $
Dựng $ AH \ bot BC, USD có $ BC \ bot A { A } ‘ \ Rightarrow BC \ bot ( { A } ‘ HA ) \ Rightarrow BC \ bot { A } ‘ H. $
Mặt khác USD BC = \ sqrt { A { { B } ^ { 2 } } + A { { C } ^ { 2 } } } = a \ sqrt { 2 } \ Rightarrow { A } ‘ H = \ frac { 2 { { S } _ { ABC } } } { BC } = \ sqrt { \ frac { 3 } { 2 } } a. $
Do $ AH = \ frac { BC } { 2 } = \ frac { a \ sqrt { 2 } } { 2 } \ Rightarrow A { A } ‘ = \ sqrt { { A } ‘ { { H } ^ { 2 } } – A { { H } ^ { 2 } } } = a. $
Thể tích khối lăng trụ là: $V={{S}_{ABC}}.A{A}’=\frac{{{a}^{3}}}{2}.$Chọn D.
| Bài tập 4: Cho khối lăng trụ đứng $ABC.{A}'{B}'{C}’$có đáy ABC là tam giác cân với $AB=AC=a$, $\widehat{BAC}=120{}^\circ ,$ mặt phẳng $(A{B}'{C}’)$ tạo với đáy một góc $60{}^\circ $. Tính thể tích V của khối lăng trụ đã cho.
A. $V=\frac{3{{a}^{3}}}{8}$ B. $V=\frac{9{{a}^{3}}}{8}$ C. $V=\frac{{{a}^{3}}}{8}$ D. $V=\frac{3{{a}^{3}}}{4}$ |
Lời giải chi tiết
Gọi M là trung điểm của USD { B } ‘ { C } ‘ $
Khi đó $ \ left \ { \ begin { matrix } { B } ‘ { C } ‘ \ bot { A } ‘ M \ \ { B } ‘ { C } ‘ \ bot A { A } ‘ \ \ \ end { matrix } \ right. \ Rightarrow { B } ‘ { C } ‘ \ bot ( { A } ‘ MA ) \ Rightarrow \ widehat { { A } ‘ MA } = 60 { } ^ \ circ USD
Ta có : USD B { { C } ^ { 2 } } = 2 { { a } ^ { 2 } } – 2 { { a } ^ { 2 } } \ cos 120 { } ^ \ circ = 3 { { a } ^ { 2 } } \ Rightarrow BC = a \ sqrt { 3 } $
USD { A } ‘ M = \ sqrt { { { a } ^ { 2 } } – { { \ left ( \ frac { a \ sqrt { 3 } } { 2 } \ right ) } ^ { 2 } } } = \ frac { a } { 2 } \ Rightarrow A { A } ‘ = h = { A } ‘ M \ tan 60 { } ^ \ circ = \ frac { a \ sqrt { 3 } } { 2 }. $
${{S}_{ABC}}=\frac{1}{2}{{a}^{2}}\sin 120{}^\circ =\frac{{{a}^{2}}\sqrt{3}}{4}\Rightarrow V={{S}_{ABC}}.A{A}’=\frac{3{{a}^{3}}}{8}.$ Chọn A.
| Bài tập 5: Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}’$có đáy ABC là tam giác cân tại A có $AB=AC=3a$. Biết rằng $A{A}’=a\sqrt{3}$và mặt phẳng $\left( {A}’BC \right)$tạo với đáy một góc $60{}^\circ $. Thể tích khối lăng trụ đã cho là:
A. ${{a}^{3}}\sqrt{6}$ B. $6{{a}^{3}}\sqrt{6}$ C. $2{{a}^{3}}\sqrt{6}$ D. $\frac{2{{a}^{3}}\sqrt{6}}{3}$ |
Lời giải chi tiết
Gọi M là trung điểm của BC, ta có $ AM \ bot BC $
Mặt khác $ BC \ bot A { A } ‘ \ Rightarrow BC \ bot \ left ( A { A } ‘ M \ right ) USD
Do đó $ \ widehat { { A } ‘ MA } = 60 { } ^ \ circ USD. Khi đó $ A { A } ‘ = AM \ tan 60 { } ^ \ circ USD
USD \ Rightarrow AM = a \ Rightarrow BM = \ sqrt { A { { B } ^ { 2 } } – A { { M } ^ { 2 } } } = 2 a \ sqrt { 2 }. $
Khi đó USD { { S } _ { ABC } } = \ frac { 1 } { 2 } BC.AM = BM.AM = 2 { { a } ^ { 2 } } \ sqrt { 2 }. $
Do đó ${{V}_{ABC.{A}'{B}'{C}’}}=A{A}’.{{S}_{ABC}}.=a\sqrt{3}.2{{a}^{2}}\sqrt{2}=2{{a}^{3}}\sqrt{6}$. Chọn C.
| Bài tập 6: Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}’$có đáy là tam giác ABC vuông tại B có $AB=a\sqrt{3},BC=a.$ Gọi M là trung điểm của AC, đường thẳng ${B}’M$ tạo với đáy một góc $45{}^\circ .$Thể tích khối lăng trụ đã cho là:
A. $\frac{{{a}^{3}}\sqrt{3}}{2}$ B. $\frac{{{a}^{3}}\sqrt{6}}{2}$ C. $\frac{{{a}^{3}}\sqrt{3}}{4}$ D. $\frac{{{a}^{3}}\sqrt{6}}{6}$ |
Lời giải chi tiết
Ta có : USD AC = \ sqrt { A { { B } ^ { 2 } } + B { { C } ^ { 2 } } } = 2 a USD .
Do vậy $ BM = \ frac { AC } { 2 } = a $ ( đặc thù trung tuyến trong tam giác vuông ) .
Lại có : USD { { S } _ { ABC } } = \ frac { 1 } { 2 } AB.AC = \ frac { { { a } ^ { 2 } } \ sqrt { 3 } } { 2 } $
Mặt khác : $ \ widehat { \ left ( { B } ‘ M ; \ left ( ABC \ right ) \ right ) } = \ widehat { { B } ‘ MB } = 45 { } ^ \ circ. $
Suy ra USD B { B } ‘ = BM \ tan 45 { } ^ \ circ = a. $
Vậy $V=B{B}’.{{S}_{ABC}}=\frac{{{a}^{3}}\sqrt{3}}{2}.$Chọn A.
| Bài tập 7: Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}’$ có tam giác ABC vuông tại B có $BC=3a$. Gọi M là trung điểm của ${A}'{C}’$ và I là giao điểm của ${A}’C$và AM. Khoảng cách từ I đến mặt phẳng $(ABC)$ bằng 2a và ${A}’B=5a$. Thể tích khối lăng trụ đã cho là:
A. $6{{a}^{3}}$ B. $2{{a}^{3}}$ C. $9{{a}^{3}}$ D. $18{{a}^{3}}$ |
Lời giải chi tiết
Do USD AM / / AC USD nên $ \ frac { I { A } ‘ } { IC } = \ frac { M { A } ‘ } { AC } = \ frac { 1 } { 2 } \ Rightarrow \ frac { { A } ‘ C } { IC } = \ frac { 3 } { 2 }. $
Do đó USD d \ left ( { A } ‘ ; \ left ( ABC \ right ) \ right ) = \ frac { 3 } { 2 } d \ left ( I ; \ left ( ABC \ right ) \ right ) = 3 a = A { A } ‘. $
Mặt khác USD AB = \ sqrt { { A } ‘ { { B } ^ { 2 } } – A { { { { A } ‘ } } ^ { 2 } } } = 4 a. $
Do đó ${{V}_{ABC.{A}'{B}'{C}’}}=A{A}’.{{S}_{ABC}}.=3a.\frac{4a.3a}{2}=18{{a}^{3}}$. Chọn D
| Bài tập 8: Cho khối lăng trụ đứng $ABC.{A}'{B}'{C}’$có đáy là tam giác ABC vuông tại A có $AB=5a,AC=12a.$ Biết rằng mặt phẳng $\left( {A}’BC \right)$ tạo với đáy một góc $60{}^\circ $. Tính thể tích khối lăng trụ $ABC.{A}'{B}'{C}’$.
A. $\frac{800{{a}^{3}}\sqrt{3}}{13}.$ B. $\frac{3600{{a}^{3}}\sqrt{3}}{13}.$ C. $\frac{900{{a}^{3}}\sqrt{3}}{13}.$ D. $\frac{1800{{a}^{3}}\sqrt{3}}{13}.$ |
Lời giải chi tiết
Dựng $ AH \ bot BC. $ Mặt khác $ A { A } ‘ \ bot BC. $
Do đó $ \ left ( { A } ‘ HA \ right ) \ bot BC. $
Khi đó $ \ widehat { \ left ( \ left ( { A } ‘ BC \ right ) ; \ left ( ABC \ right ) \ right ) } = \ widehat { { A } ‘ HA } = 60 { } ^ \ circ. $
Mặt khác USD AH = \ frac { AB.AC } { \ sqrt { A { { B } ^ { 2 } } + A { { C } ^ { 2 } } } } = \ frac { 60 } { 13 } a. $
Suy ra $ A { A } ‘ = AH \ tan \ widehat { { A } ‘ HA } = \ frac { 60 \ sqrt { 3 } } { 13 } a. $
Vậy $V=A{A}’.{{S}_{ABC}}=\frac{1800{{a}^{3}}\sqrt{3}}{13}.$ Chọn D.
| Bài tập 9: Cho khối lăng trụ đứng $ABC.{A}'{B}'{C}’$có đáy là tam giác ABC có $\widehat{BAC}=60{}^\circ ,AB=3a$và $AC=4a.$Gọi M là trung điểm của ${B}'{C}’$, biết khoảng cách từ M đến mặt phẳng $({B}’AC)$ bằng $\frac{3a\sqrt{15}}{10}$. Thể tích khối lăng trụ đã cho là:
A. ${{a}^{3}}$ B. $9{{a}^{3}}$ C. $4{{a}^{3}}$ D. $27{{a}^{3}}$ |
Lời giải chi tiết
Ta có : USD { { S } _ { ABC } } = \ frac { 1 } { 2 } AB.AC \ sin \ widehat { BAC } = 3 { { a } ^ { 2 } } \ sqrt { 3 }. $
Dựng $ BE \ bot AC ; BF \ bot { B } ‘ E. $ Khi đó $ \ left \ { \ begin { matrix } BC \ bot { B } ‘ B \ \ BC \ bot BE \ \ \ end { matrix } \ right. $
Suy ra $ BC \ bot BF \ Rightarrow BF \ bot ( { B } ‘ AC ). $
Do vậy USD d \ left ( M ; ( { B } ‘ AC ) \ right ) = BF ; BE = AB \ sin A = \ frac { 3 a \ sqrt { 3 } } { 2 }. $
Mặt khác USD d \ left ( M ; ( { B } ‘ AC ) \ right ) = \ frac { 1 } { 2 } d \ left ( C ; ( { B } ‘ AC ) \ right ) USD
USD = \ frac { 1 } { 2 } d \ left ( B ; ( { B } ‘ AC ) \ right ) = \ frac { 1 } { 2 } BF = \ frac { 3 a \ sqrt { 15 } } { 10 } \ Rightarrow BF = \ frac { 3 a \ sqrt { 15 } } { 5 } $
Mặt khác $\frac{1}{B{{F}^{2}}}=\frac{1}{B{{{{B}’}}^{2}}}+\frac{1}{B{{E}^{2}}}\Rightarrow B{B}’=3a\sqrt{3}\Rightarrow {{V}_{ABC.{A}'{B}'{C}’}}=B{B}’.{{S}_{ABC}}=27{{a}^{3}}$. Chọn D.
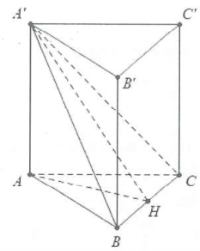
| Bài tập 10: Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}’$ có đáy ABC là tam giác vuông, AB=BC=a. Biết rằng góc giữa hai mặt phẳng $\left( AC{C}’ \right)$ và $(A{B}'{C}’)$ bằng $60{}^\circ $(tham khảo hình vẽ bên). Thể tích của khối chóp ${B}’.AC{C}'{A}’$ bằng
A. $\frac{{{a}^{3}}}{3}.$ B. $\frac{{{a}^{3}}}{6}.$ C. $\frac{{{a}^{3}}}{2}.$ D. $\frac{\sqrt{3}{{a}^{3}}}{3}.$ |
Lời giải chi tiết
Dựng USD { B } ‘ M \ bot { A } ‘ { C } ‘ \ Rightarrow { B } ‘ M \ bot \ left ( AC { C } ‘ { A } ‘ \ right ) USD
Dựng $ MN \ bot A { C } ‘ \ Rightarrow A { C } ‘ \ bot ( MN { B } ‘ ) USD
Khi đó $ \ widehat { \ left ( ( A { B } ‘ { C } ‘ ) ; \ left ( A { C } ‘ { A } ‘ \ right ) \ right ) } = \ widehat { ( MN { B } ‘ ) } = 60 { } ^ \ circ USD
Ta có : USD { B } ‘ M = \ frac { a \ sqrt { 2 } } { 2 } \ Rightarrow MN = \ frac { { B } ‘ M } { \ tan \ widehat { ( MN { B } ‘ ) } } = \ frac { a \ sqrt { 6 } } { 6 } $
Mặt khác $ \ tan \ widehat { A { C } ‘ { A } ‘ } = \ frac { MN } { { C } ‘ N } = \ frac { A { A } ‘ } { { A } ‘ { C } ‘ \, } $
Trong đó USD MN = \ frac { a \ sqrt { 6 } } { 6 }, M { C } ‘ = \ frac { a \ sqrt { 2 } } { 2 } $
USD \ Rightarrow { C } ‘ N = \ sqrt { { C } ‘ { { M } ^ { 2 } } – M { { N } ^ { 2 } } } = \ frac { a \ sqrt { 3 } } { 3 } \ Rightarrow A { A } ‘ = a $
Thể tích lăng trụ $V=\frac{A{{B}^{2}}}{2}.h=\frac{{{a}^{3}}}{2}\Rightarrow {{V}_{{B}’.AC{C}'{A}’}}=V-{{V}_{{B}’.BAC}}=V-\frac{V}{3}=\frac{2}{3}V=\frac{{{a}^{3}}}{3}.$ Chọn A.
| Bài tập 11: Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}’$ có $AB=AC=a,\widehat{ACB}=30{}^\circ ,$đường thẳng ${A}’C$ tạo với mặt phẳng $\left( AB{B}'{A}’ \right)$ một góc $45{}^\circ $. Thể tích khối lăng trụ đã cho là
A. $\frac{{{a}^{3}}\sqrt{3}}{8}$ B. $\frac{{{a}^{3}}\sqrt{6}}{8}$ C. $\frac{{{a}^{3}}\sqrt{3}}{4}$ D. $\frac{{{a}^{3}}\sqrt{6}}{4}$ |
Lời giải chi tiết
Ta có tam giác ABC cân tại A do đó $ \ widehat { B } = \ widehat { C } = 30 { } ^ \ circ USD
USD \ widehat { BAC } = 120 { } ^ \ circ. $ Dựng $ CH \ bot AB $, có $ CH \ bot A { A } ‘ $ suy ra
USD CH \ bot \ left ( AB { B } ‘ { A } ‘ \ right ) \ Rightarrow \ widehat { \ left ( C { A } ‘ ; \ left ( AB { B } ‘ { A } ‘ \ right ) \ right ) } = \ widehat { C { A } ‘ H } = 45 { } ^ \ circ USD
Mặt khác USD CH = AC \ sin \ widehat { CAH } = a \ sin 60 { } ^ \ circ = \ frac { a \ sqrt { 3 } } { 2 } $ .
Suy ra USD C { A } ‘ \ sin 45 { } ^ \ circ = CH \ Rightarrow { A } ‘ C = \ frac { a \ sqrt { 6 } } { 2 } $
USD \ Rightarrow A { A } ‘ = \ sqrt { { A } ‘ { { C } ^ { 2 } } – A { { C } ^ { 2 } } } = \ frac { a } { \ sqrt { 2 } } \ Rightarrow V = A { A } ‘. { { S } _ { ABC } } $
$=A{A}’.\frac{1}{2}AB.sin120{}^\circ =\frac{{{a}^{3}}\sqrt{6}}{8}$.Chọn B.
| Bài tập 12: Cho khối lăng trụ đứng $ABCD.{A}'{B}'{C}'{D}’$có đáy là hình chữ nhật ABCD có $AB=a,AD=a\sqrt{3}.$ Mặt phẳng $\left( {A}’BD \right)$tạo với đáy một góc $60{}^\circ $. Thể tích khối lăng trụ đã cho là:
A. $\frac{3{{a}^{3}}\sqrt{3}}{2}$ B. $\frac{3{{a}^{3}}}{2}$ C. $\frac{{{a}^{3}}}{3}$ D. $\frac{{{a}^{3}}\sqrt{3}}{2}$ |
Lời giải chi tiết
Dựng $ AH \ bot BD, $ ta có $ AH \ bot A { A } ‘ \ Rightarrow \ left ( { A } ‘ AH \ right ) \ bot BD $
Do đó $ \ widehat { \ left ( \ left ( { A } ‘ BD \ right ) ; \ left ( ABCD \ right ) \ right ) } = \ widehat { { A } ‘ HA } = 60 { } ^ \ circ USD
Mặt khác USD AH = \ frac { AB.AD } { \ sqrt { A { { B } ^ { 2 } } + A { { D } ^ { 2 } } } } = \ frac { a \ sqrt { 3 } } { 2 } $
Suy ra $ { A } ‘ A = AH \ tan 60 { } ^ \ circ = \ frac { 3 a } { 2 }, { { S } _ { ABCD } } = AB.AD = { { a } ^ { 2 } } \ sqrt { 3 } $
$\Rightarrow {{V}_{ABCD.{A}'{B}'{C}'{D}’}}=A{A}’.{{S}_{ABCD}}=\frac{3{{a}^{3}}\sqrt{3}}{2}.$ Chọn A
| Bài tập 13: Cho hình hộp chữ nhật $ABCD.{A}'{B}'{C}'{D}’$ có đáy là hình chữ nhật ABCD có $AB=3a,AD=4a.$ Đường thẳng ${A}’C$ tạo với mặt phẳng $\left( {A}'{B}’BA \right)$ một góc $30{}^\circ $. Thể tích khối hộp chữ nhật đã cho là:
A. $2{{a}^{3}}\sqrt{39}.$ B. $18{{a}^{3}}\sqrt{39}.$ C. ${{a}^{3}}\sqrt{39}.$ D. $6{{a}^{3}}\sqrt{39}.$ |
Lời giải chi tiết
Ta có : $ \ left \ { \ begin { matrix } BC \ bot AB \ \ BC \ bot { B } ‘ B \ \ \ end { matrix } \ right. \ Rightarrow BC \ bot \ left ( AB { B } ‘ { A } ‘ \ right ) USD
USD \ Rightarrow \ widehat { \ left ( { A } ‘ C ; \ left ( AB { B } ‘ { A } ‘ \ right ) \ right ) } = \ widehat { C { A } ‘ B } = 30 { } ^ \ circ USD
Khi đó USD { A } ‘ B. \ tan 30 { } ^ \ circ = BC = 4 a \ Rightarrow { A } ‘ B = 4 a \ sqrt { 3 } $
Do vậy $ { A } ‘ A = \ sqrt { { A } ‘ { { B } ^ { 2 } } – A { { B } ^ { 2 } } } = a \ sqrt { 39 } $
$\Rightarrow V={A}’A.{{A}_{ABCD}}=6{{a}^{3}}\sqrt{39}.$ Chọn D.
| Bài tập 14: Cho hình hộp chữ nhật $ABCD.{A}'{B}'{C}'{D}’$ đáy là hình chữ nhật có $AB=2a,AD=6a.$ Gọi M là trung điểm của AD, biết khoảng cách từ C đến mặt phẳng $\left( {A}’BM \right)$ bằng $\frac{12a}{7}$. Thể tích khối hộp $ABCD.{A}'{B}'{C}'{D}’$ là:
A. $24{{a}^{3}}$ B. $12{{a}^{3}}$ C. $3{{a}^{3}}$ D. $8{{a}^{3}}$ |
Lời giải chi tiết
Gọi USD I = AC \ cap BM $ ta có $ \ frac { IA } { IC } = \ frac { AM } { BC } = \ frac { 1 } { 2 } $
Do vậy USD d \ left ( C ; \ left ( { A } ‘ BM \ right ) \ right ) = 2 d \ left ( A ; \ left ( { A } ‘ BM \ right ) \ right ) = \ frac { 12 } { 7 } a. $
Dựng $AE\bot BM,AF\bot {A}’E$ khi đó
USD d \ left ( A ; \ left ( { A } ‘ BM \ right ) \ right ) = \ frac { 6 a } { 7 } = AF USD. Mặt khác
USD \ frac { 1 } { A { { E } ^ { 2 } } } + \ frac { 1 } { A { { { { A } ‘ } } ^ { 2 } } } = \ frac { 1 } { A { { F } ^ { 2 } } } \ Leftrightarrow \ frac { 1 } { A { { F } ^ { 2 } } } = \ frac { 1 } { A { { M } ^ { 2 } } } + \ frac { 1 } { A { { B } ^ { 2 } } } + \ frac { 1 } { A { { { { A } ‘ } } ^ { 2 } } } $
$\Rightarrow A{A}’=a\Rightarrow V=A{A}’.{{S}_{ABCD}}=12{{a}^{3}}$. Chọn B.
Source: http://139.180.218.5
Category: tản mạn