Bài viết này sẽ giúp các em hiểu được các biểu thức của bất đẳng thức tam giác đồng thời áp dụng nó vào làm một số câu hỏi trắc nghiệm đơn giản
QUAN HỆ GIỮA BA CẠNH CỦA MỘT TAM GIÁC.
BẤT ĐẲNG THỨC TAM GIÁC (PHẦN 1)
I/ Kiến thức cần nhớ
1. Bất đẳng thức tam giác
Định lý: Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh còn lại.
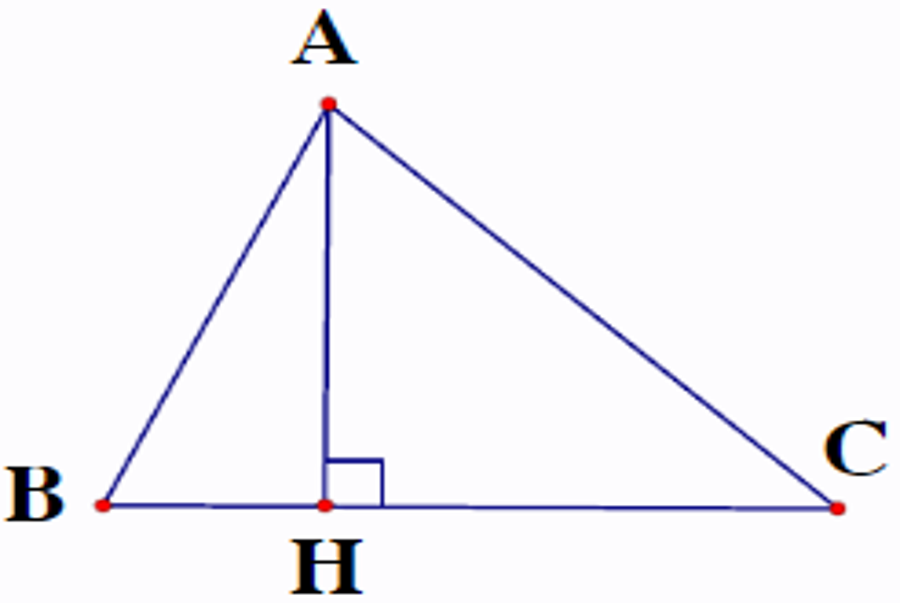
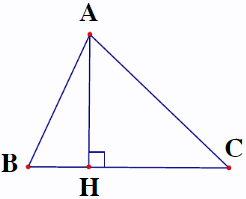
Chứng minh: Cho tam giác \(ABC.\) Chứng minh rằng: \(AB + AC > BC.\)
Kẻ \ ( AH \ bot BC \, \, \ left ( { H \ in BC } \ right ) \ )\ ( \ Rightarrow AB > HB \, \, ; \, \, AC > HC \ ) ( quan hệ giữa đường xiên và hình chiếu )\ ( \ Rightarrow AB + AC > HB + HC \ ) hay \ ( AB + AC > BC. \ ) ( đpcm ) .Chứng minh tựa như ta có : \ ( AB + BC > AC \, \, ; \, \, AC + BC > AB. \ )
2. Hệ quả của bất đẳng thức tam giác
Hệ quả: Trong một tam giác, hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại.
Chứng minh: Cho tam giác \(ABC.\) Chứng minh rằng: \(AB > BC – AC.\)
Ta có : \ ( AB + AC > BC \ ) ( định lý của bất đẳng thức tam giác )\ ( \ Rightarrow AB > BC – AC. \ )Tương tự ta có : \ ( AC > AB – BC \, \, ; \, \, BC > AB – AC \, \, ; \, \, \ )\ ( AB > AC – BC \, \, ; \, \, AC > BC – AB \, \, ; \, \, BC > AC – AB. \ )
Nhận xét: Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn lại.
Ví dụ:
Trong \ ( \ Delta ABC, \ ) ta có bất đẳng thức tam giác :\ ( \ left | { AC – AB } \ right | II/ Bài tập vận dụng
1. Bài tập trắc nghiệm
Câu 1: Cho tam giác \(ABC,\) chọn đáp án sai trong các đáp án sau:
A. \ ( AB + BC > AC \ )B. \ ( BC – AB BC \ )
Phương pháp giải:
Áp dụng bất đẳng thức tam giác .
Lời giải:
Vì trong một tam giác, độ dài một cạnh khi nào cũng lớn hơn hiệu và nhỏ hơn tổng những độ dài của hai cạnh còn lại nên những đáp án A, B, C đều đúng, đáp án D sai .
Chọn D.
Câu 2: Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của tam giác.
A. \ ( 3 cm, \, \, 5 cm, \, \, 7 cm \ ) B. \ ( 4 cm, \, \, 5 cm, \, \, 6 cm \ )C. \ ( 2 cm, \, \, 5 cm, \, \, 7 cm \ ) D. \ ( 3 cm, \, \, 6 cm, \, \, 5 cm \ )
Phương pháp giải:
Áp dụng bất đẳng thức tam giác : Trong một tam giác, tổng độ dài hai cạnh bất kể khi nào cũng lớn hơn độ dài cạnh còn lại .
Lời giải:
Chọn C.
Câu 3: Cho \(\Delta ABC\) có cạnh \(AB = 1cm\,\,;\,\,BC = 4cm.\) Tính độ dài cạnh \(AC\) biết độ dài cạnh \(AC\) là một số nguyên.
A. \ ( 1 cm \ ) B. \ ( 2 cm \ ) C. \ ( 3 cm \ ) D. \ ( 4 cm \ )
Phương pháp giải:
Áp dụng bất đẳng thức tam giác .
Lời giải:
Gọi độ dài cạnh \ ( AC \ ) là \ ( x \, \, \ left ( { cm } \ right ) \, \, \ left ( { x > 0 } \ right ). \ )Theo bất đẳng thức tam giác ta có :\ ( 4 – 1 Chọn D.
Câu 4: Cho \(\Delta ABC\) biết \(AB = 1cm\,\,;\,\,BC = 9cm\,\,;\,\,AC\) có độ dài là một số nguyên. Chu vi của tam giác \(ABC\) là:
A. \ ( 17 cm \ ) B. \ ( 18 cm \ ) C. \ ( 19 cm \ ) D. \ ( 16 cm \ )
Phương pháp giải:
+ Áp dụng bất đẳng thức trong tam giác để tính cạnh \ ( AC. \ )+ Từ đó tính chu vi tam giác \ ( ABC. \ )
Lời giải:
Gọi độ dài cạnh \ ( AC \ ) là \ ( x \, \, \ left ( { cm } \ right ) \, \, \ left ( { x > 0 } \ right ). \ )Theo bất đẳng thức tam giác ta có :\ ( 9 – 1 Chọn C.
Câu 5: Cho \(\Delta ABC\) có \(BC = 1cm\,\,;\,\,AC = 8cm\,\,;\,\,AB\) có độ dài là một số nguyên. Tam giác \(ABC\) là tam giác gì?
A. Tam giác vuông tại \ ( A. \ )B. Tam giác cân tại \ ( A. \ )C. Tam giác vuông cân tại \ ( A. \ )D. Tam giác cân tại \ ( B. \ )
Phương pháp giải:
+ Áp dụng bất đẳng thức trong tam giác để tính cạnh \ ( AB. \ )+ Từ đó xác lập đặc thù của tam giác \ ( ABC. \ )
Lời giải:
Gọi độ dài cạnh \ ( AB \ ) là \ ( x \, \, \ left ( { cm } \ right ) \, \, \ left ( { x > 0 } \ right ). \ )Theo bất đẳng thức tam giác ta có :\ ( 8 – 1 \( \Rightarrow \Delta ABC\) cân tại \(A.\)
Chọn B.
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
Source: http://139.180.218.5
Category: tản mạn