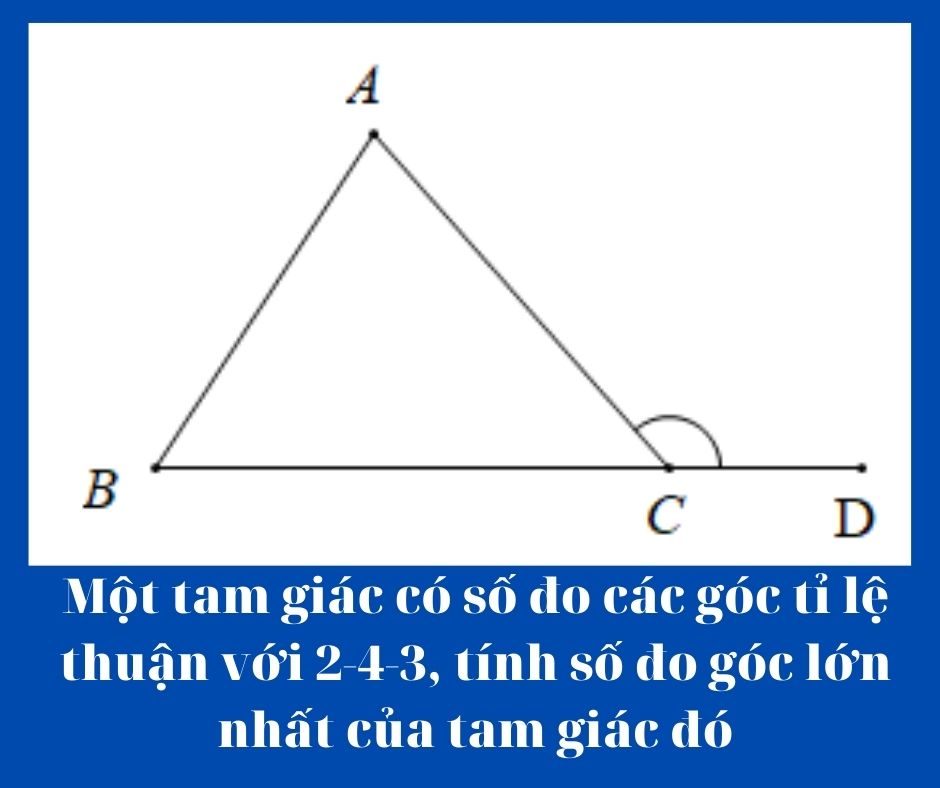
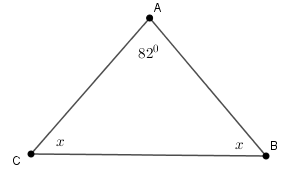
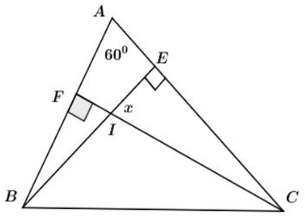
Một tam giác có số đo các góc tỉ lệ thuận với 2-4-3 tính số đo góc lớn nhất của tam giác đó

A. B ^ = 60 o

Đáp án chính xác

Áp dụng định lí tổng ba góc của một tam giác vào ΔABC, ta có: A^+B^+C^=180o

Theo đề bài ta có: A^:B^:C^=2:3:4⇒A^2=B^3=C^4
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

A^2=B^3=C^4=A^+B^+C^2+3+4=180o9=20o+)A^2=20o⇒A^=2.20o=40o+)B^3=20o⇒B^=3.20o=60o+)C^4=20o⇒C^=4.20o=80o

Vậy các góc của tam giác ABC là: A^=40o;B^=60o;C^=80o Đáp án cần chọn là A

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 10: Cho hình vẽ sau. Tính số đo x

Câu 24: Cho hình vẽ sau. Tính số đo góc x?

Câu 18: Tam giác ABC có A^=100o,B^−C^=40o. Số đo góc B và góc C lần lượt là:

Câu 12: Cho tam giác có ba góc bằng nhau. Tính số đo mỗi góc

Câu 14: Cho hình vẽ sau. Tính số đo x

Tam giác ABC có A ^ = 70 o, B ^ − C ^ = 10 o. Số đo góc B và góc C lần lượt là : Xem đáp án » 04/08/2021 1,352

Câu 28: Cho tam giác ABC. Tia phân giác của góc A cắt BC tại D. Tính số đo ADC^ biết B^−C^=20o

Câu 25: Cho hình vẽ sau. Biết EIC^=55o, tính số đo góc A

Câu 8: Cho ΔABC có A^=96o,C^=50o. Số đo góc B:

Câu 26: Cho tam giác ABC vuông ở A. Tia phân giác của góc B cắt AC tại E. Chọn câu sai:

Câu 23: Cho tam giác ABC có A^=60o,B^=12C^. Tính B^ và C^?

Câu 20: Cho tam giác ABC có A^=50o,B^=70o. Tia phân giác của góc C cắt cạnh AB tại M. Tính AMC^,BMC^

Câu 1: Tổng ba góc trong một tam giác bằng?

Câu 21: Cho tam giác ABC có B^=70o,C^=30o. Tia phân giác của góc A cắt cạnh BC tại D. Tính ADC^

Câu 4: Góc ngoài của tam giác là:

• Tải app VietJack. Xem giải thuật nhanh hơn !

Với Tính số đo góc trong tứ giác hay, chi tiết cụ thể môn Toán lớp 8 phần Hình học sẽ giúp học viên ôn tập, củng cố kiến thức và kỹ năng từ đó biết cách làm các dạng bài tập Toán lớp 8 Chương 1 : Tứ giác để đạt điểm trên cao trong các bài thi môn Toán 8.

A. Phương pháp giải. 

Sử dụng :

• Tính chất về góc của một tam giác: Tổng các góc của một tam giác bằng 1800.
• Tính chất về góc của một tứ giác: Tổng các góc của một tứ giác bằng 3600.
• Khái niệm: Hai góc bù nhau là hai góc có tổng bằng 1800.
• Tính chất của dãy tỉ số bằng nhau:

B. Ví dụ minh họa

Ví dụ 1. Tìm x ở hình 4a và hình 4b.

a ) b )

Giải

a ) Áp dụng đặc thù về tổng các góc cho tứ giác PQRS, ta được :

b ) Áp dụng đặc thù về tổng các góc cho tứ giác MNPQ ta được :

Ví dụ 2. Cho tứ giác ABCD có . Số đo góc ngoài tại đỉnh D bằng bao nhiêu?

Giải

Kéo dài tia AD ta được tia Ax, suy ra   là góc ngoài đỉnh D.

Áp dụng đặc thù về tổng các góc cho tứ giác ABCD có :

Ta thấy góc ngoài tại đỉnh D chính là góc

Vì và   là hai góc kề bù nên

Ví dụ 3. Cho tứ giác MNPQ biết:

a ) Tính các góc của tứ giác .
b ) Gọi R là giao điểm của MQ với NP. Chứng minh rằng MN / / PQ .
c ) Tính các góc của tam giác PQR .

Giải

a ) Viết lại giả thiết thành

Áp dụng đặc thù của dãy tỉ số bằng nhau và đặc thù về tổng các góc vào tứ giác MNPQ ta có :

Vậy

b )

Vì  là góc ngoài của tứ giác MNPQ tại đỉnh P, nên:

Do đó   (cặp góc ở vị trí đồng vị bằng nhau).

Vậy MN / / PQ .
c )

Theo câu b) thì  .

Ta có  là góc ngoài của tứ giác MNPQ tại đỉnh Q.

Nên

Áp dụng đặc thù về tổng các góc vào tam giác PQR, ta có :

C. Bài tập vận dụng.

Câu 1. Hãy chọn câu sai.

A. Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác.

B. Tổng các góc của một tứ giác bằng 1800 .

C. Tổng các góc của một tứ giác bằng 3600 .

D. Tứ giác ABCD là hình gồm đoạn thẳng AB, BC, CD, DA trong đó bất kỳ hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

Hiển thị đáp án

Định lý: tổng các góc của một tứ giác bằng 3600  nên C đúng, B sai.

Đáp án: B

Câu 2. Các góc của tứ giác có thể là:

A. 4 góc nhọn.

B. 4 góc tù.

C. 4 góc vuông.

D. 1 góc vuông, 3 góc nhọn.

Hiển thị đáp án
Tổng các góc trong 1 tứ giác bằng 3600 .
Các góc của tứ giác hoàn toàn có thể là 4 góc vuông vì khi đó tổng các góc của tứ giác này bằng 3600 .
Các trường hợp còn lại không thoả mãn định lý tổng các góc trong tứ giác .

Đáp án: C.

Câu 3. Cho tứ giác ABCD có  . Số đo góc C bằng:

Hiển thị đáp án

Xét tứ giác ABCD có  (định lý tổng các góc trong của một tứ giác)

Đáp án: B.

Câu 4. Cho tứ giác ABCD, trong đó . Tổng

Hiển thị đáp án

Trong tứ giác ABCD có:   (định lý tổng các góc trong của một tứ giác)

Đáp án: A.

Câu 5. Cho tứ giác ABCD có . Số đo góc ngoài tại đỉnh B bằng:

Hiển thị đáp án

Xét tứ giác ABCD có   (định lý tổng các góc trong của một tứ giác)

Nên góc ngoài tại đỉnh B có số đo là

Đáp án: A.

Câu 6. Cho tứ giác ABCD có  . Tổng số đo các góc ngoài đỉnh B, C, D bằng:

Hiển thị đáp án

Gọi góc ngoài của bốn đỉnh A, B, C, D của tứ giác ABCD lần lượt là  .

Khi đó ta có :

Ta có :

Đáp án: C.

Câu 7. Tứ giác ABCD có AB = BC, CD = DA, . Tính  .

Hiển thị đáp án

Xét tam giác ABC có AB = BC ⇒ΔABC  cân tại B có  nên

Xét tam giác ADC có CD = DA  ⇒ΔADC cân tại D có   nên

Đáp án: A.

Câu 8. Cho tứ giác ABCD biết số đo của các góc tỉ lệ thuận với 4; 3; 5; 6. Khi đó số đo các góc  lần lượt là:

Hiển thị đáp án

Vì số đo của các góc  tỉ lệ thuận với 4; 3; 5; 6 nên ta có:

( đặc thù dãy tỉ số bằng nhau )

Mà  (tính chất tổng các góc trong của tứ giác) nên ta có

Nên số đo góc lần lượt là

Đáp án: A.

Câu 9. Tam giác ABC có , các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc

Hiển thị đáp án

Kéo dài đoạn AB và AC ta được lần lượt tia Ax và Ay
Xét tam giác ABC có :

Vì BI là phân giác của

Vì CI là phân giác

Từ đó

Xét tam giác BCI có  nên

Vì BI là phân giác của

Vì BK là phân giác  

Suy ra

Tương tự ta có:  

Xét tứ giác BICK có  (tính chất tổng các góc trong của tứ giác)

Đáp án: D.