Tính cạnh huyền tam giác vuông và các dạng bài tập có lời giải từ A- Z

Bạn tốn khá nhiều thời gian để giải bài toán tính cạnh huyền của tam giác vuông cân nhưng bạn lại không biết cách tính như thế nào? Sau đây, chúng tôi chia sẻ công thức tính cạnh huyền tam giác vuông giúp bạn vận dụng giải các bài tập nhanh chóng.

Cạnh huyền là gì?

Cạnh huyền là cạnh có độ dài lớn nhất trong 3 cạnh của 1 tam giác vuông. Nói cách khác, trong một tam giác vuông cạnh đối lập với góc vuông được gọi là cạnh huyền .

Công thức tính cạnh huyền tam giác vuông

Tính cạnh huyền theo định lí Pythagor

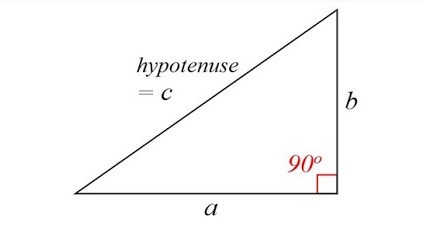
Trong định lý Pytago với một tam giác vuông bất kể có bình phương chiều dài cạnh huyền bằng tổng bình phương chiều dài hai cạnh góc vuông còn lại .

c2 = a2 + b2

Từ định lý Pytago, ta hoàn toàn có thể tính cạnh huyền tam giác vuông bằng căn bậc hai tổng bình phương chiều dài hai cạnh góc vuông còn lại

c = √(a2 + b2)

Trong đó :

• c là cạnh huyền tam giác vuông
• a, b lần lượt là 2 cạnh góc vuông còn lại

Công thức tính cạnh huyền theo định lý sin (công thức lượng giác)

Sin được dùng để chỉ tỉ số giữa những góc hoặc những cạnh trong tam giác vuông. Trong tam giác vuông, sin của một góc được xác lập bằng chiều dài của cạnh đối lập chia cho cạnh huyền .

Với mọi tam giác có canh a, b, c và những góc A, B, C thì vận dụng định lý Sin ta có công thức tính cạnh huyền tam giác vuông là :

a/sinA = b/sinB = c/sinC

Áp dụng định lý sin hoàn toàn có thể giải được mọi bài toán về tam giác nhưng để tính cạnh trong tam giác thì chỉ cạnh huyền trong tam giác vuông mới giải được bằng công thức này .

Tính cạnh huyền trong tam giác vuông đặc biệt

Chúng ta sẽ gặp 1 số ít trường hợp đặc biệt quan trọng khi đi tìm cạnh huyền của tam giác vuông như sau :

• Tam giác vuông đặc biệt có chiều dài các cạnh là bộ ba số Pitago. Bộ ba số Pitago đầu tiên là 3-4-5, vậy khi thấy hai cạnh góc vuông của một tam giác vuông là 3 và 4 thì bạn có thể suy ra ngay cạnh huyền của tam giác ấy bằng 5.
• Tam giác vuông đặc biệt có số đo ba góc là 45 độ, 45 độ và 90 độ. Tam giác này gọi là tam giác vuông cân.
• Cạnh của tam giác này có tỉ lệ 1 :1 : 1*căn2, nghĩa là 2 cạnh góc vuông bằng nhau và chiều dài cạnh huyền bằng chiều dài cạnh góc vuông nhân với căn bậc hai của 2.
• Tam giác vuông đặc biệt có số đo 3 góc là 30-60-90. Các cạnh của tam giác này có tỉ lệ là x : xcăn 3 : 2x. Nếu cho biết chiều dài 1 cạnh góc vuông thì có thể tìm ra được chiều dài huyền.

Ngoài ra, những bạn hoàn toàn có thể tìm hiểu thêm thêm công thức tính diện tích quy hoạnh tam giác cân, vuông và đều để vận dụng tính cạnh huyền nhé

Các dạng bài tập tính cạnh huyền trong tam giác vuông

Ví dụ 1: Cho một tam giác vuông có hai cạnh góc vuông lần lượt là 3cm và 4cm. Tính cạnh huyền của tam giác vuông đó.

Áp dụng công thức, cạnh huyền của tam giác vuông đó là :
c2 = 32 + 42

Vậy ta có cạnh huyền của tam giác vuông đã cho bằng 5 ( cm ) .

Ví dụ 2: Cho ∆MNP vuông tại M, biết MN = 6cm, MP = 8cm. Hỏi NP bằng bao nhiêu?

Lời giải
Theo định lý pytago ta có :
a = MN = 6 cm, b = MP = 8 cm
c2 = a2 + b2 = 62 + 82 = 36 + 64 = 100

Ví dụ 3: Giải tam giác vuông ABC vuông tại A, biết AB = 10cm, góc B bằng 300

Lời giải

Ví dụ 4: Cho tam giác ABC, trong đó BC = 11cm, . Gọi N là chân đường vuông góc hạ từ A xuống cạnh BC. Hãy tính

a ) Độ dài đoạn thẳng AN .
b ) Độ dài cạnh AC .

Lơi giải

a ) Xét tam giác vuông ANB có : AN = BN.tan 40 o
Xét tam giác vuông ANC có : AN = CN.tan 30 o
⇒ AN = BN.tan 40 o = CN.tan 30 o
Mà BN = BC – CN = 11 – CN
⇒ ( 11 – CN ). tan40o = CN.tan 30 o
⇔ ( 11 – CN ). 0,84 = CN. 0,58
⇔ 9,24 – 0,84. CN = 0,58 CN
⇔ 1,42. CN = 9,24
⇔ CN ≈ 6,51 ( cm )
⇒ AN = CN.tan 30 o ≈ 6,51. 0,58 ≈ 3,78 ( cm )
b ) Xét tam giác vuông ANC có :

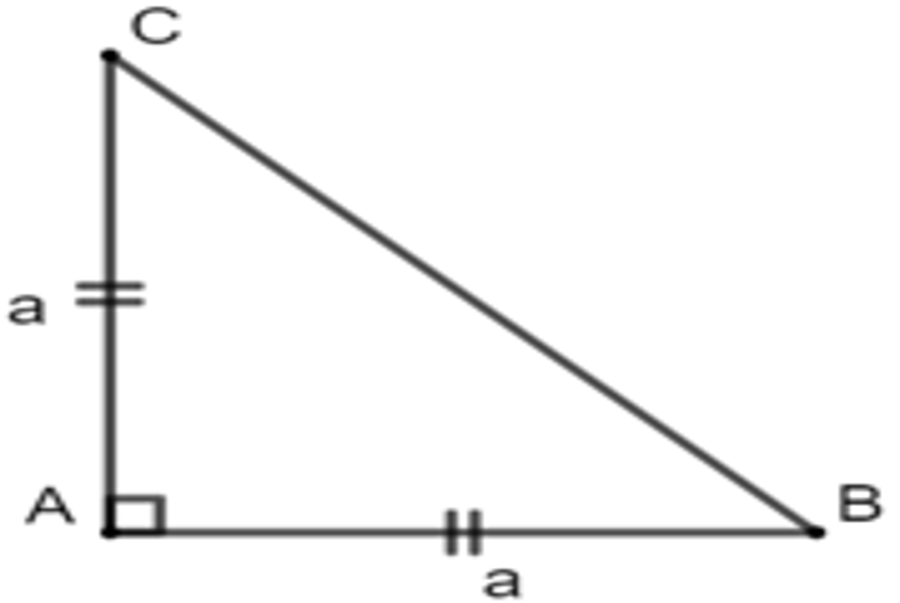
Ví dụ 5: Tính cạnh huyền và diện tích của một tam giác vuông cân nếu a là cạnh góc vuông.

Lời giải :
+ ) Xét tam giác ABC vuông cân tại A có AB = AC = a .
Áp dụng định lý Pythagor ta có :

Hy vọng với những kiến thức và kỹ năng về công thức tính cạnh huyền tam giác vuông cân mà chúng tôi vừa san sẻ giúp bạn nắm vững được kỹ năng và kiến thức để giải những bài tập từ cơ bản đến nâng cao .

1/5 – ( 1 bầu chọn )