Trong bài viết này, các em sẽ được cung cấp hai phần riêng biệt là lý thuyết và bài tập. Lý thuyết là các định nghĩa và tính chất về tứ giác mà các em đã được học trên lớp, bổ sung thêm một vài kiến thức nâng cao để củng cố. Phần bài tập là các bài tập sách giáo khoa kèm theo hướng dẫn giải chi tiết giúp các em ôn luyện lại.
Xem thêm : Tứ giác
LÝ THUYẾT VÀ BÀI TẬP TỨ GIÁC
Bạn đang đọc: Lý thuyết và bài tập tứ giác (có lời giải)
A. Lý thuyết
1. Định nghĩa
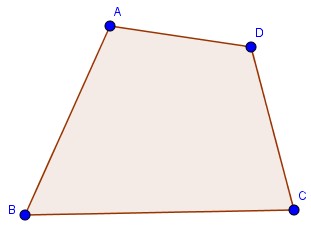
Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kỳ hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng .Tứ giác ABCD trên gọi là tứ giác lồi .Tứ giác lồi là tứ giác luôn nằm trong 50% mặt phẳng có bờ là đường thẳng chứa bất kể cạnh nào của tứ giác .
2. Tính chất
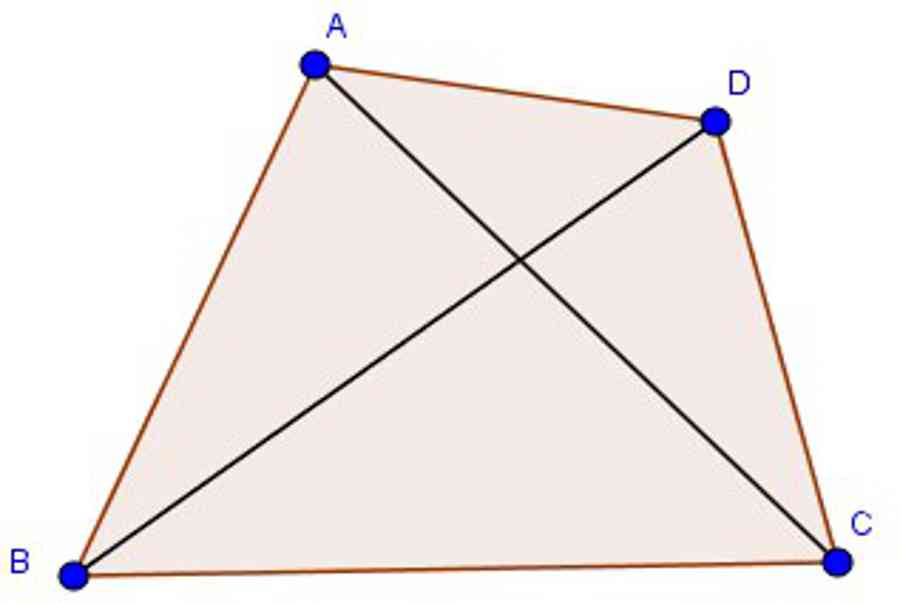
a ) Tính chất đường chéoNgười ta chứng tỏ được rằng :Trong một tứ giác lồi, hai đường chéo cắt nhau tại một điểm thuộc miền trong của tứ giác .trái lại, nếu một tứ giác có hai đường chéo cắt nhau tại một điểm thuộc miền trong của nó thì tứ giác ấy là tứ giác lồi .b ) Tính chất gócĐịnh lí :Tổng những góc của một tứ giác bằng 360 ∘ ” > 360 ∘
Chứng minh: Phương pháp chứng minh phản chứng:
“ Để chứng tỏ mệnh đề A là đúng, ta giả thiết rằng a là sai. Từ giả thiết A sai ta rút ra được Kết luận phi lí ( trái với giả thiết hoặc trái với những định lí, tiên đề hoặc trái với những Kết luận đúng mà ta có ). ” Như vậy A đúng .
B. Bài tập
Bài 1. Tìm x ở hình 5, hình 6:
Lời giải:
( Áp dụng : tổng 4 góc trong một tứ giác bằng 360 o )- Ở hình 5 :a ) x = 360 o – ( 110 o + 120 o + 80 o ) = 50 ob ) x = 360 o – ( 90 o + 90 o + 90 o ) = 90 oc ) x = 360 o – ( 90 o + 90 o + 65 o ) = 115 od ) x = 360 o – ( 75 o + 120 o + 90 o ) = 75 oVì \ ( \ angle K = 180 ^ \ circ – 60 ^ \ circ = 120 ^ \ circ \ ) ( kề bù với góc 60 o )\ ( \ angle M = 180 ^ \ circ – 105 ^ \ circ = 75 ^ \ circ \ ) ( kề bù với góc 105 o )- Ở hình 6 :a ) x + x = 360 o – ( 65 o + 95 o ) => x = 100 ob ) 2 x + 3 x + 4 x + x = 360 o=> 10 x = 360 o=> x = 36 o
Bài 2: Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.
a ) Tính những góc ngoài của tứ giác ở hình 7 a .b ) Tính tổng những góc ngoài của tứ giác ở hình 7 b ( tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài ) :
\ ( \ angle { A_1 } + \ angle { B_1 } + \ angle { C_1 } + \ angle { D_1 } \ )c ) Có nhận xét gì về tổng những góc ngoài của tứ giác ?
Lời giải:
a ) Ở hình 7 a : Góc trong còn lại :\ ( \ angle D = 360 ^ \ circ – ( 75 ^ \ circ + 90 ^ \ circ + 120 ^ \ circ ) = 75 ^ \ circ \ )Ta tính được những góc ngoài tại những đỉnh A, B, C, D lần lượt là 105 o, 90 o, 60 o, 105 ob ) Hình 7 b :Tổng những góc trong :\ ( \ angle A + \ angle B + \ angle C + \ angle D = 360 ^ \ circ \ )Nên tổng những góc ngoài :
\(\angle {A_1} + \angle {B_1} + \angle {C_1} + \angle {D_1}\)
\ ( = ( 180 ^ \ circ – \ angle A ) + ( 180 ^ \ circ – \ angle B ) + ( 180 ^ \ circ – \ angle C ) + ( 180 ^ \ circ – \ angle D ) \ )\ ( \ begin { array } { l } = 180 ^ \ circ. 4 – ( \ angle A + \ angle B + \ angle C + \ angle D ) \ \ = 720 ^ \ circ – 360 ^ \ circ = 360 ^ \ circ \ end { array } \ )c ) Nhận xét : Tổng những góc ngoài của tứ giác bằng 360 o .
Bài 3: Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình “cái diều”.
b ) Tính ∠ B, ∠ D biết rằng ∠ A = 1000 và ∠ C = 600 .
Lời giải:
a ) Ta có :AB = AD ( gt ) => A thuộc đường trung trực của BDCB = CD ( gt ) => C thuộc đường trung trực của BD
Vậy AC là đường trung trực của BDb ) Xét ΔABC và ΔADC có :AB = AD ( gt )BC = DC ( gt )AC cạnh chung=> ΔABC = ΔADC ( c. c. c )Suy ra : \ ( \ angle B = \ angle D \ )Ta có : \ ( \ angle B + \ angle D = 360 ^ \ circ – ( 100 ^ \ circ + 60 ^ \ circ ) = 200 ^ \ circ \ )Do đó : \ ( \ angle B = \ angle D = 100 ^ \ circ \ )
Bài 4. Dựa vào cách vẽ các tam giác đã học, hãy vẽ lại các tứ giác ở hình 9, hình 10 vào vở.
Lời giải:
– Cách vẽ hình 9: Vẽ tam giác ABC trước rồi vẽ tam giác ACD (hoặc ngược lại).
+ Vẽ đoạn thẳng AC = 3 cm .+ Trên cùng 50% mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 1,5 cm với cung tròn tâm C nửa đường kính 2 cm .+ Hai cung tròn trên cắt nhau tại B .+ Vẽ những đoạn thẳng AB, AC ta được tam giác ABC .Tương tự ta vẽ được tam giác ACD. Tứ giác ABCD là tứ giác cần vẽ .- Cách vẽ hình 10 : Vẽ tam giác MQP trước rồi vẽ tam giác MNP. Vẽ tam giác MQP biết hai cạnh và góc xen giữa .- Vẽ \ ( \ angle xQy = 70 ^ \ circ \ )+ Trên tia Qx lấy điểm M sao cho QM = 2 cm .+ Trên tia Qy lấy điểm P. sao cho QP = 4 cm .+ Vẽ đoạn thẳng MP, ta được tam giác MPQ .Vẽ tam giác MNP biết ba cạnh, với cạnh MP đã vẽ. Tương tự cách vẽ hình 10, điểm N là giao điểm của hai cung tròn tâm M, P. nửa đường kính lần lượt là 1,5 cm ; 3 cm .. Tứ giác MNPQ là tứ giác cần vẽ .
(*) Cách vẽ hình 10:
Bài 5. Đố. Đố em tìm thấy vị trí của “kho báu” trên hình 11, biết rằng kho báu nằm tại giao điểm các đường chéo của tứ giác ABCD, trong đó các đỉnh của tứ giác có tọa độ như sau: A(3; 2), B(2; 7), C(6; 8), D(8; 5).
Đố.
Lời giải:
Các bước làm như sau:
Đánh dấu những số thứ tự ( như trục tọa độ ) và kí hiệu những điểm như trên hình. Các bước làm như sau :- Xác định những điểm A, B, C, D trên hình vẽ với A ( 3 ; 2 ) ; B ( 2 ; 7 ) ; C ( 6 ; 8 ) ; D ( 8 ; 5 ) .- Vẽ tứ giác ABCD- Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó .- Xác định tọa độ của điểm K : K ( 5 ; 6 )
Vậy vị trí kho báu có tọa độ K(5; 6) trên hình vẽ.
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
Source: http://139.180.218.5
Category: tản mạn