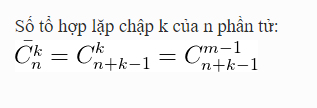Các công thức về tổ hợp

Trong Toán học, tổng hợp là cách chọn những thành phần từ một nhóm lớn hơn mà không phân biệt thứ tự. Trong những trường hợp nhỏ hơn hoàn toàn có thể đếm được số tổng hợp. Ví dụ cho ba loại quả, một quả táo, một quả cam và một quả lê, có ba cách phối hợp hai loại quả từ tập hợp này : một quả táo và một quả lê ; một quả táo và một quả cam ; một quả lê và một quả cam .

1. Tổ hợp không lặp

Cho tập A gồm n phần tử. Mỗi tập con gồm k (1≤ k ≤ n) phần tử của A được gọi là một tổ hợp chập k của n phần tử.

Theo định nghĩa, tổ hợp chập k của n phần tử là một tập con của tập hợp mẹ S chứa n phần tử, tập con gồm k phần tử riêng biệt thuộc S và không sắp thứ tự. Số tổ hợp chập k của n phần tử bằng với hệ số nhị thức.

Tổ hợp chập k của n thành phần là số những nhóm gồm k thành phần được lấy ra từ n thành phần mà giữa chúng chỉ khác nhau về thành phần cấu trúc chứ không quan trọng về thứ tự sắp xếp các thành phần. Các nhóm được coi là giống nhau nếu chúng có chung thành phần cấu trúc. VD : { 1 ; 2 ; 3 } và { 2 ; 1 ; 3 } là giống nhau .

Công thức của tổng hợp không lặp

2. Tổ hợp lặp

Cho tập A = {a1; a2; ….; an} và số tự nhiên k bất kỳ. Một tổ hợp lặp chập k của n phần tử là một tập hợp gồm k phần tử, trong đó, mỗi phần tử là một trong n phần tử của A.

Công thức của tổng hợp lặp

Các công thức về xác suất

Công thức và đặc thù của xác suất
Trong đó :

• A, B là các biến cố
• n(A): là số phần tử của biến cố A
• n (Ω): là số phần tử của không gian mẫu
• p(A): là xác suất của biến cố A
• p(B): là xác suất của biến cố B

Các dạng bài tập về tổ hợp xác suất

• Dạng 1

Ví dụ : Từ 1,2,3,4,5,6 có bao nhiêu tập hợp gồm 3 chữ số khác nhau được tạo thành .
C36 = 6 ! 6-3 ! = 7206 = 120

• Dạng 2

Ví dụ : Trong cụm thi để xét công nhận tốt nghiệp trung học phổ thông thí sinh phải thi 4 môn trong đó có 3 môn bắt buộc là Toán, Văn, ngoại ngữ và 1 môn tự chọn trong số các môn : Vật lý, Hóa học, Sinh học, Lịch sử và Địa lí. Trường X có 40 học viên ĐK dự thi, trong đó có 10 học viên chọn môn Vật lý, 20 học viên chọn môn Hóa học. Lấy 3 học viên bất kể của trường X. Tính xác suất để trong 3 học viên được chọn đó luôn có học viên chọn môn vật lý và học viên chọn môn Hóa Học .

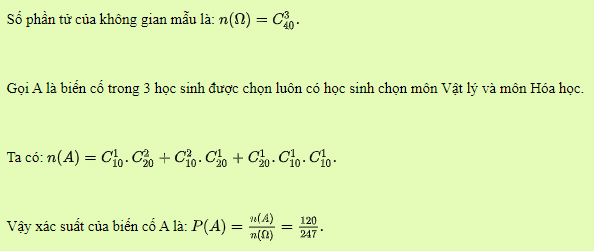
• Dạng 3

Ví dụ : Có 10 học viên, hỏi có bao nhiêu cách sắp xếp vị trí theo hàng dọc ?

• Dạng 4

Ví dụ: có 10 bạn học sinh, hỏi có bao nhiêu cách sắp xếp vị trí theo vòng tròn?

Trên đây là hàng loạt công thức và một số ít dạng bài tập về tổng hợp xác suất. Hy vọng bài viết này đã cung ứng những kỹ năng và kiến thức hữu dụng cho các em học viên, từ đó, hoàn toàn có thể vận dụng và thực hành thực tế những kỹ năng và kiến thức lượng giác thật tốt trong các bài thi, bài kiểm tra môn Toán, giúp ích cho việc học tập hàng ngày .
Ngoài ra, bạn cũng hoàn toàn có thể khám phá thêm 1 số ít kỹ năng và kiến thức học tập trên VOH .
Hình bình hành và cách tính diện tích hình bình hành : Hình bình hành là gì? Công thức tính diện tích hình bình hành ra sao? Bài viết này sẽ giúp các bạn hiểu rõ về khái niệm này.Tìm hiểu về hệ thức lượng trong tam giác : Hướng dẫn sử dụng các công thức về lượng giác trong tam giác vuông và giải những bài toán liên quan đến hệ thức.

Source: http://139.180.218.5
Category: tản mạn