1. Định nghĩa chứng minh là gì ?

Chứng minh một mệnh đề là chứng tỏ sự đúng đắn của mệnh đề đó bằng cách dựa vào những tri thức, sự kiện, chứng cứ đã biết .

Trong các hệ thống logic hình thức hóa phép chứng minh được hiểu là một chuỗi các mệnh đề (công thức) kế tiếp nhau, trong đó mỗi mệnh đề (công thức) hoặc là một tiên đề của hệ, hoặc là một mệnh đề đã được chứng minh từ trước, hoặc có thể rút ra từ một số mệnh đề (công thức) đứng trước trong chuỗi theo một quy tắc của hệ, mệnh đề cuối cùng của chuỗi là mệnh đề được chứng minh.

Phép chứng minh trong toán học cũng tương tự như như vậy : đó là một chuỗi những mệnh đề toán học, trong đó mỗi mệnh đề hoặc là một tiên đề của một mạng lưới hệ thống toán học nhất định, hoặc đã được chứng minh từ trước ( nghĩa là một định lý ), hoặc nhận được từ những mệnh đề đứng trước nó trong chuỗi theo những quy tắc logic diễn dịch nhất định. Chứng minh hiểu như trong những mạng lưới hệ thống logic hình thức và trong toán học nêu trên đây ta gọi là chứng minh theo nghĩa hẹp. Trong phép chứng minh hiểu theo nghĩa rộng, ngoài những suy luận diễn dịch còn sử dụng những suy luận khác ( quy nạp, tựa như, Phần Trăm, … ) để rút ra những mệnh đề mới từ những mệnh đề đã có sẵn .Trong logic học có một ngành, đơn cử là kim chỉ nan chứng minh, điều tra và nghiên cứu phép chứng minh hiểu theo nghĩa hẹp. Các phép chứng minh trong toán học cũng là chứng minh hiểu theo nghĩa hẹp. Nhưng khi một luật sư chứng minh sự vô tội của một bị cáo ; khi một nhà kinh tế tài chính chứng minh sự đúng đắn, tính hiệu suất cao của một kế hoạch kinh doanh thương mại ; khi một nhà xã hội học, bằng những số lượng thống kê của mình, chứng minh sự sống sót của một khuynh hướng tăng trưởng nhất định của xã hội ; khi một nhà tâm lý học, trải qua những thí nghiệm của mình, chứng minh sự sống sót của một năng lực tư duy nào đó ở khỉ đột, … thì những phép chứng minh này thường thì là chứng minh theo nghĩa rộng .

2. Cấu trúc

Phép chứng minh gồm có ba thành phần : luận đề, luận cứ và lập luận. Luận đề là mệnh đề muốn chứng minh. Luận cứ là những sự kiện, quy luật, triết lý, … mà người ta dựa vào để làm rõ tính đúng đắn của luận đề trong quy trình chứng minh. Lập luận là việc sử dụng những quy tắc logic và trình tự sắp xếp những luận cứ trong quy trình chứng minh. Nói cách khác, lập luận là cách triển khai chứng minh .

3. Một số ví dụ

Ví dụ 1. “ Lịch sử tổng thể những xã hội cho đến thời nay chỉ là lịch sử vẻ vang đấu tranh giai cấp .
Người tự do và người nô lệ, quý tộc và tầm trung, chúa đất và nông nô, thợ cả của phường hội và thợ bạn, nói Kết luận, những kẻ áp bức và những người bị áp bức, luôn luôn đối kháng với nhau, đã thực thi một cuộc đấu tranh không ngừng, lúc công khai minh bạch, lúc ngấm ngầm, một cuộc đấu tranh khi nào cũng kết thúc hoặc bằng một cuộc tái tạo cách mạng hàng loạt xã hội, hoặc bằng sự diệt vong của hai giai cấp đấu tranh với nhau .
Trong những thời đại lịch sử dân tộc tiên phong, hầu hết khắp mọi nơi, tất cả chúng ta đều thấy xã hội trọn vẹn chia thành những quý phái khác nhau, một cái thang chia thành từng nấc vị thế xã hội. Ở Rô-ma thời cổ, tất cả chúng ta thấy có quý tộc, hiệp sĩ, tầm trung, nô lệ ; thời trung cổ thì có lãnh chúa phong kiến, chư hầu, thợ cả, thợ bạn, nông nô, và hơn nữa, phần đông trong mỗi giai cấp ấy, lại có những thứ bậc đặc biệt quan trọng nữa .
Xã hội tư sản văn minh, sinh ra từ trong lòng xã hội phong kiến đã bị diệt vong, không xóa bỏ được những đối kháng giai cấp. Nó chỉ đem những giai cấp mới, những hình thức đấu tranh mới sửa chữa thay thế cho những giai cấp, những điều kiện kèm theo áp ức, những hình thức đấu tranh cũ mà thôi .
Tuy nhiên, đặc thù của thời đại tất cả chúng ta, của thời đại của giai cấp tư sản, là đã đơn giản hóa những đối kháng giai cấp. Xã hội ngày càng phân thành hai phe lớn thù địch với nhau, hai giai cấp lớn trọn vẹn trái chiều với nhau : giai cấp tư sản và giai cấp vô sản. ”Trong đoạn văn trên đây, Mác và Ăngghen đã chứng minh luận đề “ Lịch sử toàn bộ những xã hội cho đến thời nay chỉ là lịch sử dân tộc đấu tranh giai cấp ”. Để triển khai phép chứng minh này, những ông dẫn ra những chứng cứ lịch sử dân tộc như sự phân loại thành những đẳng cấp và sang trọng ở những thời đại lịch sử vẻ vang tiên phong, ở Rô-ma thời cổ, ở thời trung cổ, và sự phân loại thành giai cấp trong xã hội tư sản cùng với cuộc đấu tranh trong những hình thức khác nhau trong những thời đại lịch sử vẻ vang ấy. Suy luận mà những ông dùng ở đây là suy luận quy nạp .
Ví dụ 2. “ Cuộc cạnh tranh đối đầu sống sót là tác dụng không hề tránh được của đà tiến triển mau lẹ theo đó mọi vật hữu cơ sinh sôi nảy nở. Trong đời sống tự nhiên, mỗi vật này sinh sản nhiều trứng hay nhiều hạt, phải chịu đựng những cuộc tàn phá vào những thời kỳ, những mùa, những năm nào đó. Nếu khác thế, theo định luật sinh sản theo cấp số nhân, trong mỗi loài, số cá thể sẽ nhiều đến nỗi không một vùng nào đủ rộng để tiềm ẩn nổi. Vì số cá nhân sinh ra nhiều hơn số cá thể hoàn toàn có thể sống, vậy phải có một cuộc cạnh tranh đối đầu gắt gao hoặc giữa những cá thể của cùng một loài, hoặc giữa những cá thể thuộc những loài khác nhau, hoặc sau hết một cuộc tranh đấu chống lại những điều kiện kèm theo vật chất của đời sống. Đó là một cuộc tổng quát hóa những định luật của Malthus, vận dụng vào toàn quốc tế hữu cơ, với một sức mạnh gấp mười ; vì, trong giới sinh vật, không hề có một phương tiện đi lại nào để ngày càng tăng thực phẩm hay một cách kiêng cữ thận trọng nào trong những cuộc hôn phối. Dẫu hiện thời vài loài đang ngày càng tăng một cách mau lẹ, nhiều hay ít, nhưng đó không hề là định luật chung cho toàn thể, vì thế giới có lẽ rằng không tiềm ẩn nổi. ”
Luận đề phải chứng minh trong đoạn văn này chính là câu đầu của nó .
Ví dụ 3. “ Xin dẫn thêm vài ví dụ nữa để chứng minh sự không hàm súc và kém hiệu suất cao của phủ định. Các nhà sư phạm biết rằng, nếu chỉ cấm trẻ nhỏ làm một việc gì đó thì thật là vô ích – bày cho nó một hoạt động giải trí đơn cử hữu dụng khác mới là sáng suốt hơn. Cũng vì lý do đó, những bác sĩ tinh thần tránh những từ phủ định trong thực hành thực tế ám thị so với bệnh nhân ; thay vào đó, họ cố tạo ra cho bệnh nhân một khái niệm dương thế có năng lực loại trừ khái niệm cũ. Ta cũng biết rằng, trong 1 số ít trường hợp rối loạn hoạt động giải trí tinh thần, người bệnh khó mà hiểu được những công thức phủ định của ngôn từ – đó chính là vì đằng sau những công thức này không hề có một hình ảnh đơn cử nào hoàn toàn có thể cảm thụ bằng ngũ giác .
Hoàn toàn tựa như, trong văn học phép phủ định hiếm khi tạo được cho fan hâm mộ khái niệm dương thế. Hãy thử viết : “ anh ta tóc không vàng, mắt không xanh, không … ” – hình ảnh nhân vật sẽ bị nhòe thành một mảng không định hình. ”
Như chính tác giả đã nói, ở đoạn văn trên dây tác giả dẫn “ vài ví dụ nữa để chứng minh sự không hàm súc và kém hiệu suất cao của phủ định ”. Lập luận mà tất cả chúng ta gặp ở đây là quy nạp, từ nhiều ví dụ cho thấy tính không hàm súc và kém hiệu suất cao của phủ định đi đến Kết luận tổng quát về tính không hàm súc và kém hiệu suất cao đó .
Ví dụ 4. “ Càng gặp khó khăn vất vả, càng bồn chồn, thì bọn vua Nhà Nguyễn lại càng nghi vấn chân tay của chúng. Chúng đã ngờ và giết Nguyễn Văn Thành, chúng đã trừng trị chân tay của Lê Văn Duyệt. Bọn vua nhà Nguyễn nghi ngờ nhiều nhất những cựu thần nhà Lê hay con em của mình của họ. Đối với họ, vua nhà Nguyễn thấy rằng không dùng thì không được, mà dùng thì cũng không yên. Cuối cùng nhà Nguyễn đã dùng cựu thần nhà Lê, nhưng lại dùng bằng những thủ đoạn hung tàn để kìm hãm bọn kia làm cho bọn kia khổ sở, trớ trêu, chìm nổi trong bể loạn. Cao Bá Quát đỗ á nguyên bị đánh xuống cuối bảng, ra làm quan chưa được bao lâu đã bị không bổ nhiệm, rồi được phục chức để ở đầu cuối bị giết với những họ hàng. Nguyễn Công Trứ bị lên voi xuống chó không biết bao nhiêu lần. Nguyễn Du, Phạm Quý Thích chỉ được dùng một cách dè dặt. ”

4. Đặc điểm của chứng minh trong những khoa học xã hội và nhân văn

– Khác với phép chứng minh trong toán học và logic học, những phép chứng minh trong những khoa học khác, đặc biệt quan trọng là những phép chứng minh trong những khoa học xã hội và nhân văn, là chứng minh theo nghĩa rộng, là phép chứng minh không chỉ dựa vào những suy luận diễn dịch, mà còn dựa vào những suy luận quy nạp, Tỷ Lệ, tựa như, – những suy luận chỉ bảo vệ Kết luận có cơ sở để đáng tin cậy, nhưng không bảo vệ chắc như đinh đúng – nên không có tính ngặt nghèo tuyệt đối, mà chỉ bảo vệ một mức độ ngặt nghèo tương đối, hoàn toàn có thể đồng ý được. Nếu phép chứng minh một mệnh đề trong toán học hoặc logic học bảo vệ chắc như đinh mệnh đề đó đúng, không hề phản bác được, thì phép chứng minh mệnh đề trong những khoa học xã hội và nhân văn ( và nhiều khoa học khác ) không bảo vệ chắc như đinh tính đúng đắn của mệnh đề. Phép chứng minh ở đây chỉ có tính thuyết phục nhiều hay ít mà thôi. Chính vì thế cách triển khai chứng minh, số lượng và cách sử dụng những sự kiện và tri thức đã biết có một tầm quan trọng rất lớn trong những phép chứng minh này .

– Ở những phép chứng minh trong khoa học xã hội và nhân văn, các luận cứ thường được dẫn ra cùng với sự lý giải, giải thích nguyên nhân (xem ví dụ 2, 3 trong mục 3).

5. Các giải pháp chứng minh

Các giải pháp chứng minh hoàn toàn có thể chia thành hai loại : chứng minh trực tiếp và chứng minh gián tiếp .

a. Chứng minh trực tiếp

Chứng minh trực tiếp là phép chứng minh trong đó từ tính chân thực của những luận cứ rút ra tính chân thực của luận đề mà không dùng đến phản luận đề .
Ví dụ 5. Có sáu người, trong đó hai người bất kể nào cũng hoặc là bạn của nhau, hoặc là quân địch của nhau. Ta chứng minh rằng trong số sáu người này có 3 người là bạn lẫn nhau, hoặc có 3 người là quân địch lẫn nhau .
Giải. Gọi A là một người trong số 6 người đã nêu. Trong 5 người còn lại phải có tối thiểu 3 người bạn của A, hoặc có tối thiểu 3 quân địch của A, vì nếu cả số bạn và số thù của A đều nhỏ hơn 3 thì tổng số của họ nhỏ hơn 5. Với trường hợp 1, ta gọi 3 người trong số bạn của A là B, C, D. Nếu trong số này có một cặp nào đó là bạn của nhau thì cùng với A họ hợp thành nhóm 3 người bạn lẫn nhau. Ngược lại, nếu trong 3 người B, C, D không ai là bạn của ai thì họ chính là nhóm 3 người thù lẫn nhau. Với trường hợp có tối thiểu 3 quân địch của A chứng minh tựa như .
Phương pháp chứng minh trực tiếp chỉ sử dụng thông tin có trong những luận cứ nên khó triển khai, thường hay lạc hướng .

b. Chứng minh gián tiếp

Chứng minh gián tiếp là phép chứng minh trong đó từ tính chân thực của những luận cứ rút ra tính giả dối của phản luận đề, rồi từ đây rút ra tính chân thực của luận đề. Trong phép chứng minh gián tiếp, vì có sử dụng thông tin chứa trong phản luận đề nên ít khi bị lạc hướng, dễ thực thi hơn .
Hai giải pháp chứng minh gián tiếp thường gặp là chứng minh bằng phản chứng và chứng minh phân liệt. Khi chứng minh bằng phản chứng một luận đề, người ta xuất phát từ giả định nó sai, nghĩa là phản luận đề đúng. Từ đây, cùng với những luận cứ người ta đi đến một nghịch lý. Nghịch lý này chứng tỏ điều giả định là sai, và như vậy điều ngược lại với nó – tức là luận đề – đúng. Chứng minh bằng phản chứng có sơ đồ như sau .
Gọi B1, B2, …, Bn là những luận cứ, A là luận đề, C là mệnh đề nào đó, khi đó :

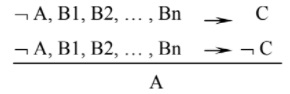
Trong sơ đồ này nếu từ giả định phản luận đề ¬ A và những luận cứ B1, B2 ,
…, Bn vừa hoàn toàn có thể rút ra mệnh đề C nào đó, vừa hoàn toàn có thể rút ra phủ định của C, tức là ¬ C, thì hoàn toàn có thể rút ra luận đề A .Ví dụ 6. Nếu 7 n + 3 là số lẻ thì n là số chẵn .
Chứng minh : Giả sử luận đề đã cho sai. Khi đó 7 n + 3 là số lẻ, nhưng n là số lẻ. Vì n lẻ nên n = 2 k – 1, với k là số tự nhiên nào đó. Khi đó 7 n + 3 = 7 ( 2 k – 1 ) + 3 = 14 k – 4 = 2 ( 7 k – 2 ). Như vậy 7 n + 3 là số chẵn. Điều này xích míc với giả định 7 n + 3 lẻ. Vậy không hề nói luận đề đã cho sai, hay nói cách khác, luận đề đã cho đúng .
Chứng minh bằng phản chứng là chiêu thức chứng minh rất thường được sử dụng trong toán học và những nghành nghề dịch vụ khác. Tuy nhiên trong logic thiết kế và toán học thiết kế, toán học trực giác, chiêu thức chứng minh này lại không được đồng ý. Điều này tương quan đến quan điểm về sự sống sót của những đối tượng người dùng lý tưởng, trong những ngành khoa học vừa nêu, đối tượng người dùng được coi là sống sót khi và chỉ khi hoàn toàn có thể chỉ ra chiêu thức thiết kế xây dựng nó qua 1 số ít bước hữu hạn .
Chứng minh phân liệt là chứng minh một mệnh đề tuyển có chứa luận đề và vô hiệu tổng thể những năng lực, ngoại trừ năng lực của luận đề. Nói cách khác, đây là phép chứng minh dựa trên quy tắc tam đoạn luận lựa chọn :

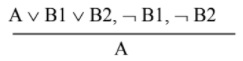
Ví dụ 7. Có một vụ cháy trong thành phố. Cơ quan tìm hiểu chứng minh rằng nguyên do gây ra vụ cháy này là thiếu cẩn trọng khi đun nấu. Vì quy trình tìm hiểu trước hết đã cho thấy rằng nguyên do của vụ cháy này là do thiếu cẩn trọng khi đun nấu, hoặc do sự cố về điện, hoặc do có kẻ cố ý đốt. Sau đó đã xác lập được thêm rằng lúc xảy ra vụ cháy này không hề có sự cố về điện nào, nguyên do có kẻ cố ý đốt cũng bị loại trừ, vậy chỉ còn lại năng lực cháy do không cẩn thận khi đun nấu .
Khi vận dụng chiêu thức chứng minh phân liệt trong những nghành của đời sống cần phải đặc biệt quan trọng chú ý quan tâm đến tính chân thực của tiền đề dạng tuyển. Chính vì trong đời sống trong thực tiễn nhiều khi không hề bảo vệ tính chân thực tuyệt đối của những mệnh đề dạng này nên tính thuyết phục của chứng minh phân liệt bị hạn chế. Đây cũng chính là nguyên do làm cho chứng minh phân liệt chỉ được đồng ý một cách hạn chế trong hoạt động giải trí tư pháp. Chẳng hạn, TANDTC không hề đồng ý phép chứng minh phân liệt để buộc tội cho một bị cáo trong câu truyện sau đây. Trên một hòn hòn đảo nọ chỉ có 3 người A, B, C. Người C bị giết chết. Thủ phạm giết người chỉ là A hoặc B. Cơ quan tìm hiểu xác lập được rằng A không phải là thủ phạm, vậy chắc như đinh B là thủ phạm .

(Nguồn tài liệu: Phạm Đình Nghiêm, Nhập môn logic học)

Source: http://139.180.218.5
Category: tản mạn