Hiểu rõ bản chất công thức và cẩn thận với các lỗi sai đáng tiếc sẽ giúp học sinh xử lý tốt dạng toán về diện tích hình vuông, hình chữ nhật.

Bài toán tính diện tích là nội dung cơ bản, phổ cập ở mảng hình học, Toán lớp 3. Tuy nhiên, do mới làm quen về chủ đề này, nhiều học viên chưa nắm rõ thực chất cũng như dễ mắc lỗi cơ bản khi làm bài. Để nắm chắc kiến thức và kỹ năng hơn trong dạng bài này học viên hãy tìm hiểu thêm ngay phần bài giảng chi tiết cụ thể của cô Nguyễn Thị Hoa, giáo viên Toán tại Hocmai. vn nhé .

Kiến thức tổng quát về bài toán tính diện tích hình vuông, hình chữ nhật.

1. Bản chất của đơn vị Xăng-ti-mét vuông

Đối với khối học viên tiểu học, khi học Toán cần có những hình ảnh trực quan và đơn thuần nhất ngay từ những yếu tố nhỏ để tiếp thu kỹ năng và kiến thức nhanh hơn .
Với mục tiêu để học viên hiểu được cách thiết kế xây dựng công thức tính diện tích, cô Hoa đã phân phối kiến thức và kỹ năng về đơn vị chức năng sử dụng tính diện tích cơ bản nhất : Xăng-ti-mét vuông .

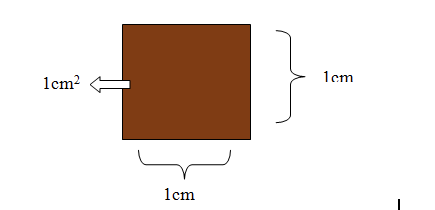
Khái niệm: Xăng-ti-mét vuông là diện tích của một hình vuông với độ dài cạnh bằng 1cm.

Viết tắt: cm2

Quy ước: Xăng-ti-mét vuông – cm2  là đơn vị để đo diện tích.

2. Diện tích hình vuông

Xác định công thức: Để tính diện tích hình vuông, ta chia hình thành các hình vuông nhỏ có cạnh bằng 1cm. Vậy, diện tích hình vuông đã cho sẽ bằng đổng diện tích các hình vuông nhỏ (diện tích bằng 1cm2) cộng lại.

• Diện tích hình vuông = Tổng những hình vuông đơn vị chức năng ( diện tích bằng 1 cm2) .
• Tổng những hình vuông đơn vị chức năng = Số hình vuông ở 1 hàng ngang x Số hình vuông ở 1 hàng dọc ( = chiều dài cạnh x chiều rộng cạnh của hình vuông lớn )

Ví dụ: Tính diện tích hình vuông có cạnh là 5 cm

Ta có : 5 x 5 = 25 ( cm2 ) .

Kết luận: Muốn tính diện tích hình vuông, ta lấy số đo một cạnh nhân với chính nó.

S.ABCD = a x a ( ABCD là hình vuông, a là độ dài một cạnh ) .

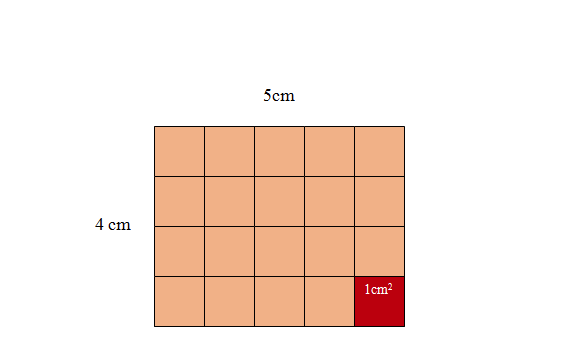
Minh họa hình vuông có cạnh 5 cm

3. Diện tích hình chữ nhật

Xác định công thức: Tương tự cách tính diện tích hình vuông, ta chia nhỏ hình chữ nhật thành các hình vuông có diện tích bằng 1cm2.

• Diện tích hình chữ nhật = Tổng những hình vuông đơn vị chức năng ( diện tích bằng 1 cm2) .
• Tổng những hình vuông đơn vị chức năng = Số hình vuông ở 1 hàng ngang x Số hình vuông ở 1 hàng dọc ( = chiều dài x chiều rộng của hình chữ nhật )

Xét ví dụ: Tính diện tích hình chữ nhật có chiều dài bằng 5cm, chiều rộng bằng 4cm. Vậy, diện tích hình chữ nhật cần tìm bằng 5 x 4 = 20cm2.

Kết luận:  Muốn tính diện tích hình chữ nhật, ta lấy chiều dài nhân chiều rộng của hình đó.

SCDEG = a x b ( CDEG là hình chữ nhật có chiều dài cạnh bằng a, chiều rộng bằng b )

4. Công thức suy rộng

Từ những công thức tìm được, Cô Hoa cũng hướng dẫn học viên cách suy ngược công thức để ship hàng cho những bài thống kê giám sát ngược ( biết diện tích, nhu yếu tính những cạnh ) :

Chiều dài = Diện tích : Chiều rộng

Chiều rộng = Diện tích : Chiều dài

Các lỗi sai thường gặp và lưu ý khi làm bài toán tính diện tích

Với kinh nghiệm tay nghề lâu năm trong giảng dạy, từng gặp nhiều sai sót trong bài làm của học viên, cô Hoa đã tổng hợp 1 số ít quan tâm để học trò tránh được những sai lầm đáng tiếc này :
1 – Các đại lượng phải cùng đơn vị chức năng đo : Đối với những bài toán đơn thuần, đề bài thường cho sẵn những đại lượng cùng đơn vị chức năng, tuy nhiên ở 1 số ít bài toán khó hơn, học viên cần quan tâm kiểm tra đơn vị chức năng đo những cạnh ( đại lượng ) có cùng đơn vị chức năng hay chưa, nếu chưa ta cần đổi để đưa chúng về cùng đơn vị chức năng với nhau .
2 – Ghi sai đơn vị chức năng tính : Vì đơn vị chức năng đo của diện tích với độ dài chỉ khác nhau một chút ít ở kí hiệu mũ ( 2 ) trên đầu, vì vậy học viên cần cẩn trọng kiểm tra cách ghi đơn vị chức năng đã đúng hay chưa, không được bỏ lỡ phần ghi đáp số rất đầy đủ đơn vị chức năng .

Trên đây là bài giảng chi tiết và cách tính, bản chất công thức và một số lưu ý giải toán về diện tích.

Thông qua video bài giảng về diện tích hình vuông và hình chữ nhật, cô Nguyễn Thị Hoa mong ước giúp học viên hiểu được thực chất của phép tính, tránh học thuộc máy móc gây nhầm lẫn khi học thêm nhiều những loại công thức khác nhau .
Nắm vững cơ sở kim chỉ nan giám sát còn giúp học viên hiểu sâu, kỹ lưỡng để nhanh gọn thích nghi với những dạng toán hình học nâng cao hơn .

Source: http://139.180.218.5
Category: tản mạn