Bài 1
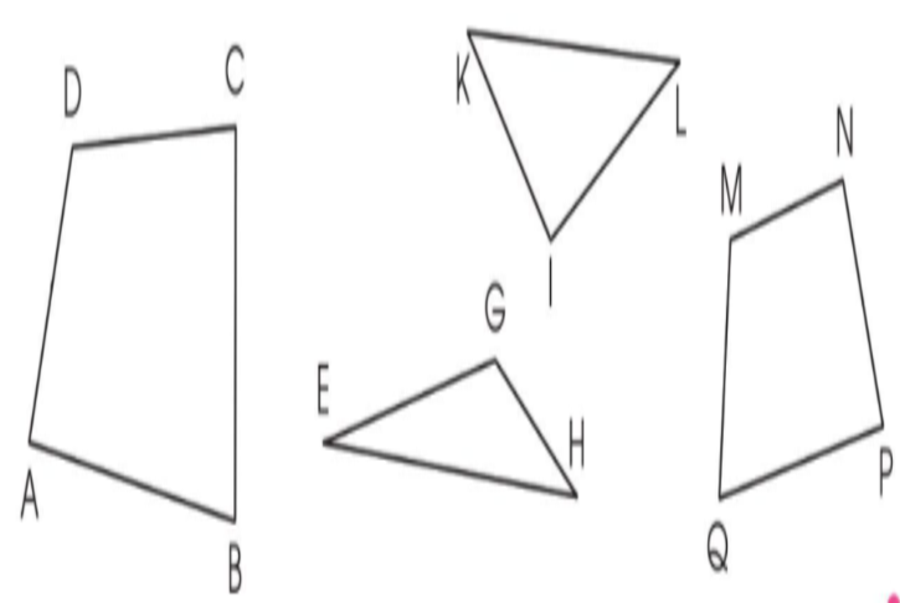
Nêu tên hình và các đỉnh, cạnh, góc có trong mỗi hình dưới đây.
Phương pháp giải:
Quan sát hình vẽ rồi nêu tên những hình, những đỉnh và những cạnh, góc của mỗi hình đó .
Lời giải chi tiết:
– Hình tam giác KIL :
+ 3 đỉnh là : K, I, L
+ 3 cạnh là : KI, IL, LK
+ 3 góc là : Góc đỉnh K, cạnh KI và KL
Góc đỉnh I, cạnh IK và IL
Góc đỉnh L, cạnh LI và LK
– Hình tam giác GEH :
+ 3 đỉnh là : G, E, H
+ 3 cạnh là : GE, EH, HG
+ 3 góc là : Góc đỉnh G, cạnh GE, GH
Góc đỉnh E, cạnh EG, EH
Góc đỉnh H, cạnh HE, HG
– Hình tứ giác ADCB :
+ 4 đỉnh là A, D, C, B
+ 4 cạnh là AD, DC, CB, BA
+ 4 góc là : Góc đỉnh A, cạnh AD và AB
Góc đỉnh D, cạnh DA và DC
Góc đỉnh C, cạnh CD và CB
Góc đỉnh B, cạnh BC và BA
– Hình tứ giác QMNP :
+ 4 đỉnh là : Q., M, N, P
+ 4 cạnh là : QM, MN, NP, PQ
+ 4 góc là : Góc đỉnh Q., cạnh QM và QP
Góc đỉnh M, cạnh MN và MQ
Góc đỉnh N, cạnh NM và NP
Góc đỉnh P, cạnh PN và PQ
Bài 2
Quan sát hình vẽ, triển khai những hoạt động giải trí sau :
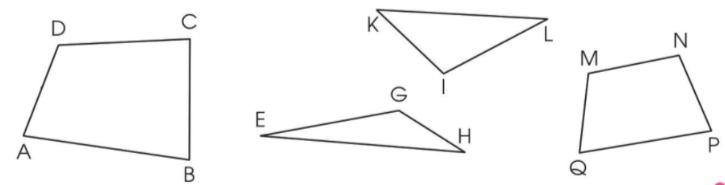
a ) Đọc tên những hình tam giác, hình tứ giác ở trên .
b) Dùng ê ke để kiểm tra và nêu tên góc vuông, góc không vuông trong mỗi hình trên.
Phương pháp giải:
a ) Hình tam giác ABC .
Hình tứ giác GHIE, hình tứ giác LMNK .
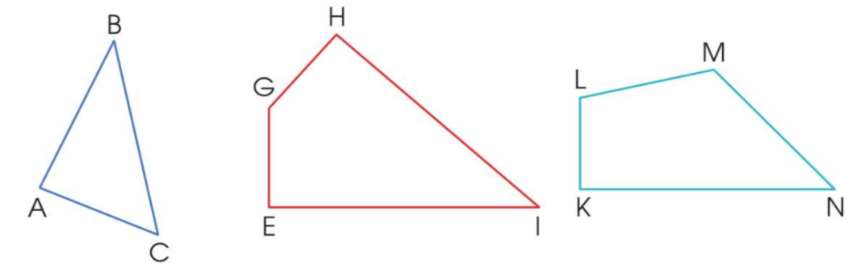
b) Hình tam giác ABC:
– Góc vuông đỉnh A, cạnh AB và AC
– Góc không vuông đỉnh B, cạnh BA và BC
– Góc không vuông đỉnh C, cạnh CA và CB
Hình tứ giác GHIE:
– Góc không vuông đỉnh G, cạnh GH và GE
– Góc không vuông đỉnh I, cạnh IH và IE
– Góc vuông đỉnh E, cạnh EG và EI
– Góc vuông đỉnh H, cạnh HG, HI
Hình tứ giác LMNK:
– Góc vuông đỉnh K, canh KL và KN
– Góc không vuông đỉnh L, cạnh LM và LK
– Góc không vuông đỉnh M, cạnh MN và ML
– Góc không vuông đỉnh N, cạnh NM và NK
Bài 3
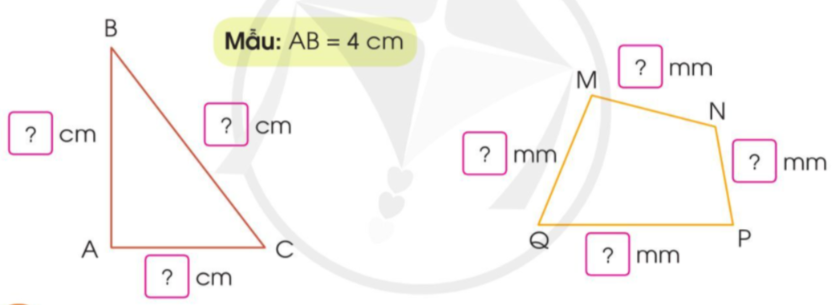
Đo độ dài mỗi cạnh của hình tam giác, hình tứ giác sau rồi viết số đo ( theo mẫu ) :
Phương pháp giải:
Sử dụng thước có vạch chia để đo độ dài những cạnh của hình tam giác và hình tứ giác.
Bài 4
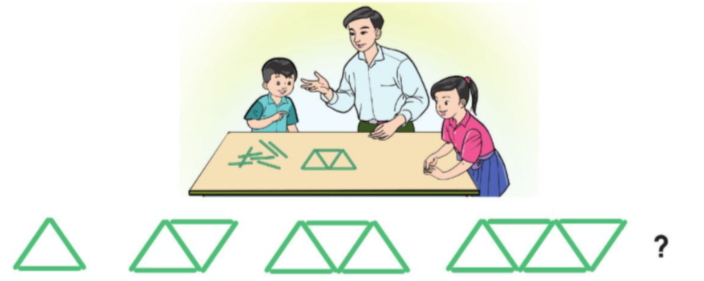
Theo em, hình tiếp theo ( ? ) được ghép bởi bao nhiêu que tính ?
Phương pháp giải:
Quan sát hình vẽ ta nhận thấy quy luật : Hình phía sau nhiều hơn hình phía trước 2 que tính .
Từ đó em vấn đáp được câu hỏi ở đề bài .
Lời giải chi tiết:
Hình thứ nhất gồm 3 que tính .
Hình thứ hai gồm 5 que tính .
Hình thứ ba gồm 7 que tính .
Hình thứ tư gồm 9 que tính .
Vậy ta nhận thấy quy luật: Hình phía sau nhiều hơn hình phía trước 2 que tính.
Vậy hình tiếp theo có 11 que tính.
Source: http://139.180.218.5
Category: tản mạn