I. HÌNH CHÓP LÀ GÌ?

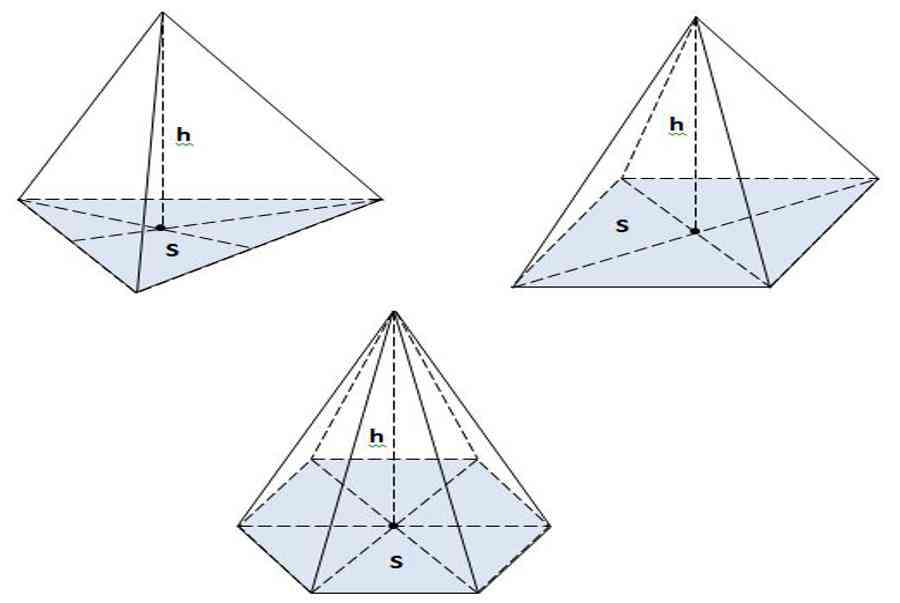
Trong hình học khoảng trống, hình chóp là khối đa diện trong đó có mặt dưới của hình là đa giác lồi. Các mặt bên là các tam giác có chung một đỉnh, đây chính là đỉnh của hình chóp .Tính chất của hình chóp là :

• Đường thẳng đi qua một đỉnh và vuông góc với mặt phẳng đáy tương ứng được gọi là đường cao của hình chóp.
• Tên gọi của hình chóp được dựa vào đa giác mặt đáy: Hình chóp tam giác có đáy là hình tam giác, hình chóp tứ giác có đáy là hình tứ giác, hình chóp ngũ giác có đáy là hình ngũ giác…
• Nếu hình chóp có các cạnh bên hợp với mặt đáy các góc bằng nhau hoặc các cạnh bên bằng nhau thì chân đường cao của hình chóp chính là tâm đường tròn ngoại tiếp mặt đáy hình chóp.
• Nếu hình chóp có các mặt bên hợp với mặt đáy các góc bằng nhau hoặc có các đường cao của các mặt bên xuất phát từ 1 đỉnh bằng nhau thì chân đường cao là tâm đường tròn nội tiếp mặt đáy hình chóp.
• Nếu hình chóp có mặt bên hoặc mặt chéo vuông góc với mặt phẳng đáy thì đường cao của hình chóp sẽ là đường cao của mặt bên hoặc mặt chéo đó.

Ví dụ: Hình chóp tam giác có đáy là hình tam giác, hình chóp tứ giác có đáy là hình tứ giác, hình chóp ngũ giác có đáy là hình ngũ giác…

II. DIỆN TÍCH HÌNH CHÓP

Công thức tính diện tích xung quanh hình chóp đứng như sau:

Ta có diện tích quy hoạnh xung quanh hình chóp bằng nửa chu vi đáy hình chóp nhân với độ dài trung đoạn của hình chóp ( trung đoạn là đường cao xuất phát từ đỉnh xuống trung điểm của 1 cạnh ) .

\(S_{xq}=p.d\)

Trong đó :

• \(S_{xq}\): diện tích xung quanh hình lăng trụ chóp.
• p: nửa chu vi đáy hình chóp.
• d: độ dài trung đoạn của hình chóp (trung đoạn là đường cao xuất phát từ đỉnh xuống trung điểm của 1 cạnh).

Công thức tính diện tích toàn phần hình chóp như sau:

Ta có diện tích quy hoạnh toàn phần hình chóp bằng tổng của diện tích quy hoạnh xung quanh hình chóp cộng với diện tích quy hoạnh đáy hình chóp .

\(S_{tp}=S_{xq}+S_{đ}\)

Trong đó :

• \(S_{tp}\): diện tích toàn phần hình chóp.
• \(S_{xq}\): diện tích xung quanh hình chóp.
• \(S_{đ}\): diện tích đáy hình chóp.

III. THỂ TÍCH HÌNH CHÓP 

Công thức tính thể tích hình chóp như sau:

Để tính thể tích hình chóp ta lấy diện tích quy hoạnh đáy nhân với chiều cao hình chop từ đỉnh xuống đáy sau đó nhân với 1/3 .

\(V={1\over{3}}.S_{đ}.h\)

Trong đó :

• V: thể tích hình chóp.
• \(S_{đ}\): diện tích đáy hình chóp.
• h: chiều cao hình chóp

IV. BÀI TẬP THAM KHẢO DIỆN TÍCH VÀ THỂ TÍCH HÌNH CHÓP

Ví dụ: Tính thể tích và diện tích xung quanh của hình chóp tam giác S.ABC có △ABC vuông tại B, AH ∈ (SBC), AH ⊥(ABC) biết AB = 4a, BC = 3a, AC = 5a, SH= 6a.

Lời giải tham khảo:

Áp dụng công thức tính thể tích của hình chóp, ta có thể tích của hình chóp đã cho là :

\(V={1\over{3}}.S_{đ}.h={1\over{3}}.6a.{1\over{2}}.4a.3a= 12a^3\)

Nửa chu vi đáy hình chóp S.ABC : p = ( 4 a + 3 a + 5 a ) : 2 = 6 aÁp dụng công thức tính diện tích quy hoạnh xung quanh hình chóp, ta có diện tích quy hoạnh xung quanh hình chóp đã cho là :\ ( S_ { xq } = p. d = 6 a. 6 a = 36 a ^ 2 \ )

Source: http://139.180.218.5
Category: tản mạn