Điểm thuộc đường cố định (Phần 1)

Byadnhacly

Th3 24, 2022

Đây là phần thuận của bài toán quỹ tích, một dạng toán khó và rất rộng. Trong bài viết nhỏ này tôi xin trình diễn 1 số ít bước để giải bài toán và 1 số ít ví dụ minh họa .
Điểm thuộc đường cố định và thắt chặt, thì hoàn toàn có thể thuộc đường thẳng hoặc đường tròn, đôi lúc số lượng giới hạn trong đoạn thẳng hoặc cung tròn. Do đó ta cần trang bị 1 số ít kiến thức và kỹ năng cơ bản về quỹ tích 1 số ít đường hay gặp :
Quỹ tích là đường thẳng .

Quỹ tích các đường thẳng cách đều hai điểm là đường trung trực.
Quỹ tích cách đều hai cạnh của một góc là phân giác của góc đó.
Quỹ tích các điểm cách một đường thẳng một khoảng cho trước là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng đã cho.
Điểm thuộc đường thẳng qua hai điểm cố định, qua một điểm cố định vuông góc hoặc song song với một đường cố định…

Trong một số trường hợp ta chỉ cần chứng minh điểm thuộc đường cố định nào đó, ta lại quy về việc chứng minh ba điểm thẳng hàng.

Bạn đang đọc: Điểm thuộc đường cố định (Phần 1)

Ta biết được điểm thuộc đường thẳng hay đường tròn thường ta phải Dự kiến bằng cách cho 3 trường hợp phân biệt, trong đó có những trường hợp đặc biệt quan trọng. Nếu không vẽ thêm hình thì yên cầu người làm toán phải có trực giác và cảm nhận hình học tốt. Sau khi Dự kiến được thì ta dùng những kỹ năng và kiến thức đã biết để tìm giải thuật .
Sau đây ta xem một vài ví dụ sau .

Ví dụ 1. Cho đường tròn tâm $O$ đường kính $AB = 2R$. $CD$ là đường kính thay đổi, $AC, AD$ cắt tiếp tuyến tại $B$ của $(O)$ tại các điểm $P, Q$. Chứng minh rằng $CDQP$ nội tiếp và tâm đường tròn ngoại tiếp của tứ giác thuộc một đường cố định.

Gợi ý

Bước Dự kiến, ta hoàn toàn có thể vẽ hình đúng mực cho $ CD $ đổi khác rồi dựng điểm USD I USD, khi vẽ hình chích xác ta xác lập được những điểm USD I $ sẽ cùng thuộc một đường thẳng .
Đến lúc này, ta hãy liên hệ đường thẳng mà ta phát hiện với những yếu tố có trên hình đó là USD O $, đường tròn USD ( O ) USD, $ AB $ và tiếp tuyến tại USD B $ .
Nếu phát hiện được đường thẳng đó song song với tiếp tuyến tại $ B $ thì ta hãy liên hệ với những quỹ tích hay gặp để tìm ra đặc thù .

Ta có $\angle ACD = \angle ABD = \angle AQP$, suy ra $BPCQ$ nội tiếp.
Gọi $I$ là tâm đường tròn ngoại tiếp tứ giác. Ta có $IM \bot PQ, IO \bot CD$.
Mặt khác, ta có $AM \bot CD, AO \bot PQ$.
Khi đó $IM ||AO, IO ||AM$, suy ra $AOIM$ là hình bình hành. Suy ra $IM = AO$ không đổi.
Hơn nữa $IM \bot PQ$ và $I, A$ khác phía đối với $PQ$ do đó $I$ thuộc đường thẳng song song với $PQ$ và cách $PQ$ một khoảng bằng bán kính và khác phía $A$ đối với $PQ$.

Ví dụ 2. Cho đường tròn $(O)$ và điểm $A$ nằm ngoài đường tròn, một cát $d$ tuyến qua $A$ cắt $(O)$ tại hai điểm $C, D$. Tiếp tuyến tại $C, D$ cắt nhau tại $P$, chứng minh $P$ luôn thuộc một đường thẳng cố định khi $d$ thay đổi và luôn qua $A$.

Gợi ý

Chỉ cần vẽ hình đúng mực ta hoàn toàn có thể xác lập ngay rằng $ P $ thuộc một đường thẳng vuông góc với USD AO $, như nhận xét trên, để chứng minh đường thẳng này cố định và thắt chặt ta chỉ cần chứng minh nó đi qua một điểm cố định và thắt chặt nào đó, việc này thuận tiện khi hoàn toàn có thể chứng minh điểm đó thuộc USD OA USD. Từ đó có cách giải sau :
Gọi $ H $ là hình chiếu của $ P $ trên USD AO USD. Ta chứng minh $ H $ cố đinh. Gọi USD I $ là giao điểm của $ OP $ và $ CD $ .
Ta có $ OI.OP = OC ^ 2 $ không đổi .
USD \ triangle OPH \ backsim OIA $, suy ra $ OH.OA = OI.OP = OC ^ 2 $ không đổi. Mà $ O, A $ cố định và thắt chặt, suy ra $ H $ có định .
Do đó $ P $ thuộc đường thẳng vuông góc với $ OA $ tại USD H USD cố định và thắt chặt .

Ví dụ 3. (PTNK 2004) Cho đường tròn tâm $O$ bán kính $R$ và điểm $A$ nằm ngoài đường tròn. Một đường thẳng thay đổi qua $A$ cắt $(O)$ tại $B, C$. Chứng minh rằng tâm đường tròn ngoại tiếp tam giác $OBC$ luôn thuộc một đường thẳng cố định.

Xem thêm: #99 STT Anh Em, Cap về tình anh em trong xã hội chất nhất – Babelgraph

Gợi ý

Đây là một bài toán khó, nhưng cách giải của nó cũng là kinh nghiệm tay nghề cho những bài toán khác .

Nhận thấy rằng đường tròn ngoại tiếp tam giác $ OBC $ đi qua một điểm cố định và thắt chặt là USD O USD, khi đó để chứng minh tâm USD I $ của đường tròn này thuộc một đường thẳng cố định và thắt chặt, một cách tâm lý tự nhiên là cần chứng minh thêm nó đi qua một điểm cố định và thắt chặt khác, khi đó sẽ nằm trên đường trung trực của đoạn thẳng nối $ O $ và điểm kia .
Nếu vẽ hình đúng chuẩn, ta hoàn toàn có thể Dự kiến được đường thẳng đó vuông góc với đường $ OA USD cố định và thắt chặt, khi đó ta hoàn toàn có thể nghĩ đến cách như ví dụ 2, vẽ $ OH \ bot OA $ và chứng minh $ OH $ không đổi .
Nói chung tùy cách tâm lý ta hoàn toàn có thể đi tìm giải thuật .

Gọi $D$ là giao điểm của $AO$ và $(OBC)$.
Ta có $AD.AO = AB.AC = AH^2 = OA^2 – R^2$ không đổi, suy ra $D$ cố định.
Do đó tâm $I$ của $(OBC)$ thuộc đường trung trực của đoạn $OD$.

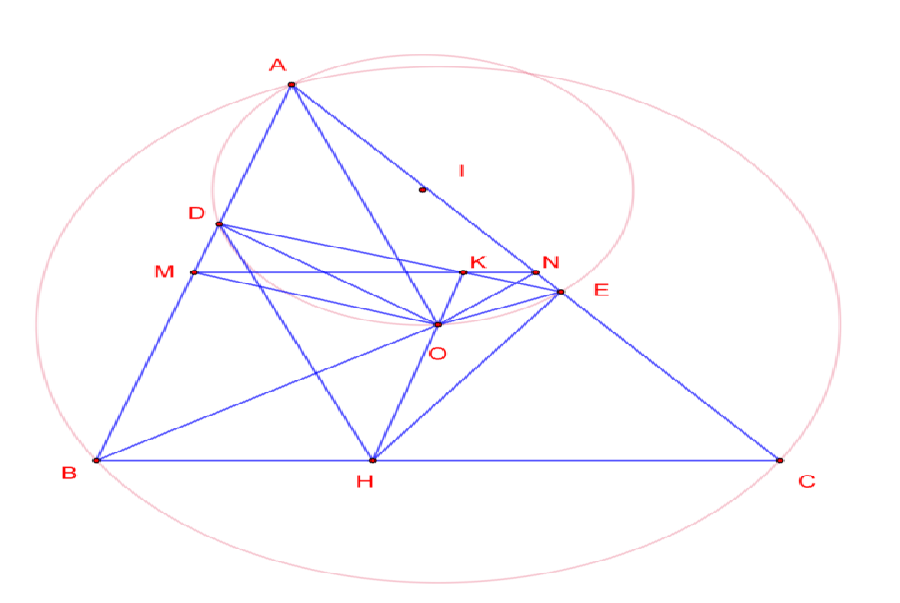
Ví dụ 4. Cho tam giác $ABC$, tâm ngoại tiếp là $(O)$. Một đường tròn thay đổi qua $A, O$ cắt các cạnh $AB, AC$ tại $D, E$.

a. Chứng minh rằng hình chiếu của $ O $ trên $ DE $ thuộc một đường thẳng cố định và thắt chặt .
b. Chứng minh rằng trực tâm tam giác $ ODE $ thuộc một đường thẳng cố định và thắt chặt .

Gợi ý

Gọi USD K $ là hình chiếu của $ O $ trên USD DE USD. Ta thấy $ ADOE $ nội tiếp và USD K $ là hình chiếu $ O $ trên USD DE $, quy mô quen thuộc, gợi ý cho ta đến một định lý khá quen thuộc .

a .

Gọi $M, N$ là hình chiếu của $O$ trên $AB, AC$, ta có $M, N$ là trung điểm của $AB, AC$ nên cố định.
Theo định lý Simson thì $M, K, N$ thẳng hàng, hay $K$ thuộc đường thẳng $MN$ cố định.

b .
Nếu vẽ hình đúng mực, ta hoàn toàn có thể dựđoán được trực tâm $ H $ của tam giác $ ODE $ thuộc đường thẳng $ BC USD cố định và thắt chặt, do đó ta chỉ cần chứng minh $ B, H, C $ thẳng hàng, ta lại quay về việc chứng minh 3 điểm thẳng hàng .

Ta có $\angle OHD = \angle OED = \angle OAD = \angle OBA$, suy ra $ODBH$ nội tiếp.
Tương tự ta có $OECH$ nội tiếp.
Khi đó $\angle OHB = \angle ODA = \angle OEC = 180^\circ – \angle OHC$. Suy ra $B, H, C$ thẳng hàng.
Vậy $H$ thuộc đường thẳng $BC$ cố định.

Bài tập rèn luyện.

Cho đoạn thẳng $AB$ và điểm $M$ thỏa $MA^2 – MB^2 = k$ không đổi. Chứng minh rằng $M$ thuộc một đường thẳng cố định.
Cho tam giác $ABC$, đường tròn thay đổi qua $B, C$ cắt các cạnh $AB, AC$ tại $D, E$. Chứng minh rằng tâm đường tròn ngoại tiếp tam giác $ADE$ luôn thuộc một đường thẳng cố định.
Cho tam giác $ABC$ vuông tại $A$ với $B, C$ cố định. Đường cao $AH$, gọi $D, E$ là hình chiếu của $H$ trên $AB, AC$. Đường tròn đường kính $AH$ cắt đường tròn ngoại tiếp tam giác $ABC$ tại $P$. Gọi $Q$ là giao điểm của $AP$ và $DE$. Chứng minh $Q$ thuộc một đường cố định.
Cho đường tròn $(O)$ cố định và điểm $A$ nằm trong đường tròn, đường thẳng thay đổi qua $A$ cắt $(O)$ tại $B$ và $C$. Gọi $D$ là giao điểm hai tiếp tuyến tại $B$ và $C$ của $(O)$. Chứng minh rằng $D$ thuộc một đường cố định.
Cho tam giác $ABC$ cân tại $A$ nội tiếp đường tròn $(O)$. $D$ là một điểm thay đổi trên cạnh $BC$. Đường tròn $(I)$ qua $D$ và tiếp xúc với cạnh $AB$ tại $B$; đường tròn $(J)$ qua $D$ tiếp xúc với cạnh $AC$ tại $C$. Chứng minh rằng trung điểm của $IJ$ luôn thuộc một đường cố định.
Cho hình chữ nhật $ABCD$. Gọi $H$ là hình chiếu vuông góc của $A$ trên $BD$. $M$ là điểm thay đổi trên đoạn $BH$. Đường tròn ngoại tiếp tam giác $ADM$ cắt $CD$ tại điểm $N$. Chứng minh rằng trung điểm của $MN$ luôn thuộc một đường thẳng cố định.

Nội dung chính