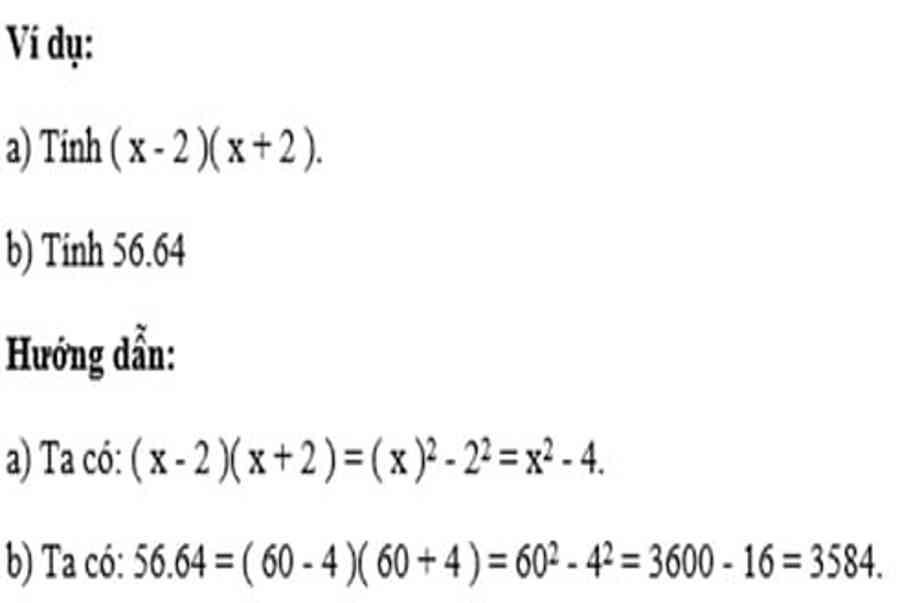Những hằng đẳng thức đáng nhớ chắc không còn xa lạ gì với các bạn. Hôm nay Kiến sẽ nói kỹ hơn về 7 hằng đẳng thức quan trọng : bình phương của một tổng, bình phương của một hiệu, hiệu của hai bình phương, lập phương của một tổng, lập phương của một hiệu, tổng hai lập phương và cuối cùng là hiệu hai lập phương. Các bạn cùng tham khảo nhé.

Bạn đang xem : Tổng bình phương là gì

A. 7 hằng đẳng thức đáng nhớ

1. Bình phương của một tổng

Với A, B là các biểu thức tùy ý, ta có: ( A + B )2= A2+ 2AB + B2.

Ví dụ:

a) Tính ( a + 3 )2.b) Viết biểu thức x2+ 4x + 4 dưới dạng bình phương của một tổng.a ) Tính ( a + 3 ) 2. b ) Viết biểu thức x2 + 4 x + 4 dưới dạng bình phương của một tổng .

Hướng dẫn:

a ) Ta có : ( a + 3 ) 2 = a2 + 2. a. 3 + 32 = a2 + 6 a + 9. b ) Ta có x2 + 4 x + 4 = x2 + 2. x. 2 + 22 = ( x + 2 ) 2 .

2. Bình phương của một hiệu

Với A, B là các biểu thức tùy ý, ta có: ( A – B )2= A2- 2AB + B2.

3. Hiệu hai bình phương

Với A, B là các biểu thức tùy ý, ta có: A2- B2= ( A – B )( A + B ).

4. Lập phương của một tổng

Với A, B là các biểu thức tùy ý, ta có: ( A + B )3= A3+ 3A2B + 3AB2+ B3.

5. Lập phương của một hiệu.

Với A, B là các biểu thức tùy ý, ta có: ( A – B )3= A3- 3A2B + 3AB2- B3.

Ví dụ :

a) Tính ( 2x – 1 )3.b) Viết biểu thức x3- 3x2y + 3xy2- y3dưới dạng lập phương của một hiệu.a ) Tính ( 2 x – 1 ) 3. b ) Viết biểu thức x3 – 3×2 y + 3 xy2 – y3dưới dạng lập phương của một hiệu .

Hướng dẫn:

a) Ta có: ( 2x – 1 )3a ) Ta có : ( 2 x – 1 ) 3= ( 2 x ) 3 – 3. ( 2 x ) 2.1 + 3 ( 2 x ). 12 – 13= 8×3 – 12×2 + 6 x – 1b) Ta có : x3- 3x2y + 3xy2- y3b ) Ta có : x3 – 3×2 y + 3 xy2 – y3= ( x ) 3 – 3. x2. y + 3. x. y2 – y3= ( x – y ) 3

6. Tổng hai lập phương

Với A, B là các biểu thức tùy ý, ta có: A3+ B3= ( A + B )( A2- AB + B2).

Chú ý : Ta quy ước A2 – AB + B2là bình phương thiếu của hiệu A – B .Xem thêm : Hình Ảnh Mới Nhất Của Tử Tù Dương Chí Dũng ‘ Đưa Ông Ngọ 500

Ví dụ:

a) Tính 33+ 43.b) Viết biểu thức ( x + 1 )( x2- x + 1 ) dưới dạng tổng hai lập phương.a ) Tính 33 + 43. b ) Viết biểu thức ( x + 1 ) ( x2 – x + 1 ) dưới dạng tổng hai lập phương .

Hướng dẫn:

a ) Ta có : 33 + 43 = ( 3 + 4 ) ( 32 – 3.4 + 42 ) = 7.13 = 91. b ) Ta có : ( x + 1 ) ( x2 – x + 1 ) = x3 + 13 = x3 + 1 .

7. Hiệu hai lập phương

Với A, B là các biểu thức tùy ý, ta có: A3- B3= ( A – B )( A2+ AB + B2).

Chú ý : Ta quy ước A2 + AB + B2là bình phương thiếu của tổng A + B .

Ví dụ:

a) Tính 63- 43.b) Viết biểu thức ( x – 2y )( x2+ 2xy + 4y2) dưới dạng hiệu hai lập phươnga ) Tính 63 – 43. b ) Viết biểu thức ( x – 2 y ) ( x2 + 2 xy + 4 y2 ) dưới dạng hiệu hai lập phương

Hướng dẫn:

a) Ta có: 63- 43= ( 6 – 4 )( 62+ 6.4 + 42) = 2.76 = 152.b) Ta có : ( x – 2y )( x2+ 2xy + 4y2) = ( x )3- ( 2y )3= x3- 8y3.

B. Bài tập tự luyện về hằng đẳng thức

a ) Ta có : 63 – 43 = ( 6 – 4 ) ( 62 + 6.4 + 42 ) = 2.76 = 152. b ) Ta có : ( x – 2 y ) ( x2 + 2 xy + 4 y2 ) = ( x ) 3 – ( 2 y ) 3 = x3 – 8 y3 .

Bài 1.Tìm x biết

a) ( x – 3 )( x2+ 3x + 9 ) + x( x + 2 )( 2 – x ) = 0.b) ( x + 1 )3- ( x – 1 )3- 6( x – 1 )2= – 10.a ) ( x – 3 ) ( x2 + 3 x + 9 ) + x ( x + 2 ) ( 2 – x ) = 0. b ) ( x + 1 ) 3 – ( x – 1 ) 3 – 6 ( x – 1 ) 2 = – 10 .

Hướng dẫn:

a) Áp dụng các hằng đẳng thức ( a – b )( a2+ ab + b2) = a3- b3.a ) Áp dụng những hằng đẳng thức ( a – b ) ( a2 + ab + b2 ) = a3 – b3 .( a – b ) ( a + b ) = a2 – b2 .Khi đó ta có ( x – 3 ) ( x2 + 3 x + 9 ) + x ( x + 2 ) ( 2 – x ) = 0 .⇔ x3 – 33 + x ( 22 – x2 ) = 0 ⇔ x3 – 27 + x ( 4 – x2 ) = 0⇔ x3 – x3 + 4 x – 27 = 0⇔ 4 x – 27 = 0Vậy x =b) Áp dụng hằng đẳng thức ( a – b )3= a3- 3a2b + 3ab2- b3b ) Áp dụng hằng đẳng thức ( a – b ) 3 = a3 – 3 a2b + 3 ab2 – b3( a + b ) 3 = a3 + 3 a2b + 3 ab2 + b3( a – b ) 2 = a2 – 2 ab + b2Khi đó ta có : ( x + 1 ) 3 – ( x – 1 ) 3 – 6 ( x – 1 ) 2 = – 10 .⇔ ( x3 + 3×2 + 3 x + 1 ) – ( x3 – 3×2 + 3 x – 1 ) – 6 ( x2 – 2 x + 1 ) = – 10⇔ 6×2 + 2 – 6×2 + 12 x – 6 = – 10⇔ 12 x = – 6Vậy x =

Bài 2:Rút gọn biểu thức A = (x + 2y ).(x – 2y) – (x – 2y)2

2×2+ 4xy B. – 8y2+ 4xy- 8y2 D. – 6y2+ 2xy2x2 + 4 xy B. – 8 y2 + 4 xy – 8 y2 D. – 6 y2 + 2 xy

Hướng dẫn

Ta có : A = ( x + 2 y ). ( x – 2 y ) – ( x – 2 y ) 2A = x2 – ( 2 y ) 2 –

A = x2– 4y2– x2+ 4xy – 4y22

A = – 8 y2 + 4 xyHãy nhớ nó nhé

Những hằng đẳng thức đáng nhớ trên rất quan trọng tủ kiến thức của chúng ta. Thế nên các bạn hãy nghiên cứu và ghi nhớ nó nhé. Những đẳng thức đó giúp chúng ta xử lý các bài toán dễ và khó một cách dễ dàng, các bạn nên làm đi làm lại để bản thân có thể vận dụng tốt hơn. Chúc các bạn thành công và chăm chỉ trên con đường học tập. Hẹn các bạn ở những bài tiếp theo

Source: http://139.180.218.5
Category: tản mạn