Xem toàn bộ tài liệu Lớp 9: tại đây

Xem thêm các sách tham khảo liên quan:

Sách Giải Sách Bài Tập Toán 9 Bài 1 : Căn bậc hai giúp bạn giải những bài tập trong sách bài tập toán, học tốt toán 9 sẽ giúp bạn rèn luyện năng lực suy luận hài hòa và hợp lý và hợp logic, hình thành năng lực vận dụng kết thức toán học vào đời sống và vào những môn học khác :

Bài 1 trang 5 Sách bài tập Toán 9 Tập 1: Tính căn bậc hai số học của:

a. 0,01     b. 0,04     c. 0,49     d. 0,64

e. 0,25 f. 0,81 g. 0,09 h. 0,16

Lời giải:

a. √ 0,01 = 0,1 vì 0,1 ≥ 0 và ( 0,1 ) 2 = 0,01
b. √ 0,04 = 0,2 vì 0,2 ≥ 0 và ( 0,2 ) 2 = 0,04
c. √ 0,49 = 0,7 vì 0,7 ≥ 0 và ( 0,7 ) 2 = 0,49
d. √ 0,64 = 0,8 vì 0,8 ≥ 0 và ( 0,8 ) 2 = 0,64
e. √ 0,25 = 0,5 vì 0,5 ≥ 0 và ( 0,5 ) 2 = 0,25
f. √ 0,81 = 0,9 vì 0,9 ≥ 0 và ( 0,9 ) 2 = 0,81
g. √ 0,09 = 0,3 vì 0,3 ≥ 0 và ( 0,3 ) 2 = 0,09
h. √ 0,16 = 0,4 vì 0,4 ≥ 0 và ( 0,4 ) 2 = 0,16

Bài 2 trang 5 Sách bài tập Toán 9 Tập 1: Dùng máy tính bỏ túi tim x thỏa mãn đẳng thức (làm tròn đến chữ số thập phân thứ ba).

a. x2 = 5 b. x2 = 6
c. x2 = 2,5 d. x2 = √ 5

Lời giải:

a. x2 = 5 ⇒ x1 = 5 và x2 = – 5
Ta có : x1 = 5 ≈ 2,236 và x2 = – 5 = – 2,236
b. x2 = 6 ⇒ x1 = 6 và x2 = – 6
Ta có : x1 = 6 ≈ 2,449 và x2 = – 6 = – 2,449
c. x2 = 2,5 ⇒ x1 = √ 2,5 và x2 = – √ 2,5
Ta có : x1 = √ 2,5 ≈ 1,581 và x2 = – √ 2,5 = – 1,581
d. x2 = 5 ⇒ x1 = √ ( √ 5 ) và x2 = √ ( √ 5 )
Ta có : x1 = √ ( √ 5 ) ≈ 1,495 và x2 = – √ ( √ 5 ) = – 1,495

Bài 3 trang 5 Sách bài tập Toán 9 Tập 1: Số nào có căn bậc hai là:

a. √ 5 b. 1,5 c. – 0,1 d. – √ 9

Lời giải:

a. Số 5 có căn bậc hai là √ 5
b. Số 2,25 có căn bậc hai là 1,5
c. Số 0,01 có căn bậc hai là – 0,1
d. Số 9 có căn bậc hai là – √ 9

Bài 4 trang 5 Sách bài tập Toán 9 Tập 1: Tìm x không âm biết:

a. √ x = 3 b. √ x = √ 5 c. √ x = 0 d. √ x = – 2

Lời giải:

a. √ x = 3 ⇒ x = 32 ⇒ x = 9
b. √ x = √ 5 ⇒ x = ( √ 5 ) 2 ⇒ x = 5
c. √ x = 0 ⇒ x = 02 ⇒ x = 0
d. Căn bậc hai số học là số không âm nên không sống sót giá trị nào của √ x thỏa mãn nhu cầu x = – 2

Bài 5 trang 6 Sách bài tập Toán 9 Tập 1: So sánh (không dùng bảng số hay máy tính bỏ túi)

a. 2 và √ 2 + 1 b. 1 và √ 3 – 1
c. 2 √ 31 và 10 d. – √ 3.11 và – 12

Lời giải:

a. Ta có : 1 < 2 ⇒ √ 1 < √ 2 ⇒ 1 < √ 2
Suy ra : 1 + 1 < √ 2 + 1
Vậy 2 < √ 2 + 1 b. Ta có : 4 > 3 ⇒ √ 4 > √ 3 ⇒ 2 > √ 3
Suy ra : 2 – 1 > √ 3 – 1
Vậy 1 > √ 3 – 1
c. Ta có : 31 > 25 ⇒ √ 31 > √ 25 ⇒ √ 31 > 5
Suy ra : 2. √ 31 > 2.5

Vậy 2.√31 > 10

d. Ta có : 11 < 16 ⇒ √ 11 < √ 16 ⇒ √ 11 < 4 Suy ra : – 3. √ 11 > – 3.4
Vậy – 3 √ 11 > – 12

Bài 6 trang 6 Sách bài tập Toán 9 Tập 1: Tìm những khẳng định đúng trong các khẳng định sau:

a. Căn bậc hai của 0,36 là 0,6
b. Căn bậc hai của 0,36 là 0,06
c. √ 0,36 = 0,6
d. Căn bậc hai của 0,36 là 0,6 và – 0,6
e. √ 0,36 = ± 0,6

Lời giải:

Câu a và c đúng .

Lời giải:

Căn bậc hai số học của 25 là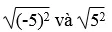

Bài 8 trang 6 Sách bài tập Toán 9 Tập 1: Chứng minh: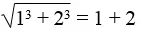

Viết tiếp 1 số ít đẳng thức tựa như .

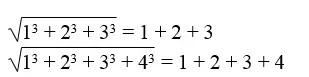
Lời giải:

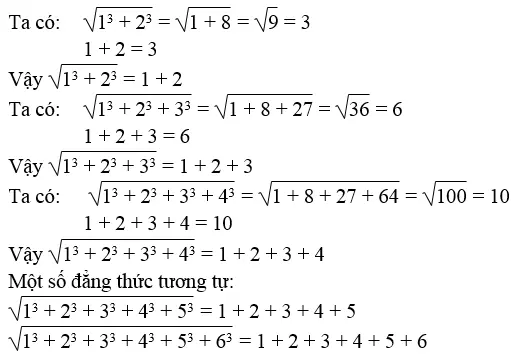
Bài 9 trang 6 Sách bài tập Toán 9 Tập 1: Cho hai số a, b không âm. Chứng minh:

a. Nếu √ a < √ b thì a < b
b. Nếu a < b thì √ a < √ b

Lời giải:

a. a ≥ 0 ; b ≥ 0 và a < b ⇒ b > 0

Ta có : √ a ≥ 0 ; √ b ≥ 0 suy ra : √ a + √ b > 0 ( 1 )
Vì a < b nên a – b < 0
Suy ra : ( √ a + √ b ) ( √ a – √ b ) < 0 ( 2 )
Từ ( 1 ) và ( 2 ) suy ra : √ a – √ b < 0 ⇒ √ a < √ b
b. a ≥ 0 ; b ≥ 0 và √ a < √ b ⇒ √ b > 0
Suy ra : √ a + √ b > 0 và √ a – √ b < 0
( √ a + √ b ) ( √ a – √ b ) < 0
⇒ ( √ a ) 2 – ( √ b ) 2 < 0 ⇒ a – b < 0 ⇒ a < b

Bài 10 trang 6 Sách bài tập Toán 9 Tập 1: Cho số m dương. Chứng minh:

a. Nếu m > 1 thì √ m > 1 b. Nếu m < 1 thì √ m < 1

Lời giải:

a. Ta có : m > 1 ⇒ √ m > √ 1 ⇒ √ m > 1
b. Ta có : m < 1 ⇒ √ m < √ 1 ⇒ √ m < 1

Bài 11 trang 6 Sách bài tập Toán 9 Tập 1: Cho số m dương. Chứng minh:

a. Nếu m > 1 thì m > √ m b. Nếu m < 1 thì m < √ m

Lời giải:

a. Ta có : m > 1 ⇒ √ m > √ 1 ⇒ √ m > 1
Vì m > 0 nên √ m > 0
Suy ra : √ m. √ m > 1. √ m ⇒ m > √ m
b. Ta có : m < 1 ⇒ √ m < √ 1 ⇒ √ m < 1 Vì m > 0 nên √ m > 0
Suy ra : √ m. √ m < 1. √ m ⇒ m < √ m

Bài 1 trang 7 Sách bài tập Toán 9 Tập 1: Giá trị của √0,16 là

A. 0,04 ;
B. 0,4 ;
C. 0,04 và – 0,04

D. 0,4 và -0,4.

Lời giải:

Chọn đáp án B

Source: http://139.180.218.5
Category: tản mạn