Trong chương trình hình học THPT, các bài tập về thể tích khối chóp luôn xuất hiện trong đề thi đại học. Vì vậy, học sinh cần nắm chắc các kiến thức cơ bản về khối chóp và thuộc nằm lòng công thức tính thể tích khối chóp. Cùng VUIHOC ôn tập lý thuyết và điểm lại 12 công thức tính thể tích khối chóp thường sử dụng nhé! 

1. Ôn tập triết lý thể tích khối chóp lớp 12

Thể tích của một vật là lượng khoảng trống mà vật ấy chiếm. Thể tích thường có đơn vị chức năng đo là lập phương của khoảng cách .

Trong chương trình học, thể tích khối chóp được tính theo công thức : USD V = \ frac { 1 } { 3 } \ frac { 1 } { 3 }. S.h $ $ với S là diện tích quy hoạnh đáy, h là chiều cao .
Ngoài ra, để ship hàng cho những bài tập tính tỉ số thể tích hai khối chóp tam giác thường Open trong những bài toán ôn tập thể tích khối chóp lớp 12, ta có thêm công thức :
Nếu A ’, B ’, C ’ là ba điểm lần lượt nằm trên những cạnh SA, SB, SC của hình chóp tam giác S.ABC thì khi đó :

2. Các công thức tính thể tích khối chóp dễ hiểu nhất

Nhìn chung, có rất nhiều những giải pháp và công thức dùng để tính được thể tích khối chóp, đồng thời vận dụng thể tích khối chóp nâng cao. Tuy nhiên, trong bài ôn tập này, VUIHOC chỉ tổng hợp 12 công thức tính thể tích khối chóp thường gặp và dễ sử dụng nhất để giải những bài toán hình học có tương quan đến thể tích khối chóp .

2.1. Cách tính thể tích khối chóp có mặt bên vuông góc đáy

Để nhận diện những bài toán thể tích hình chóp vận dụng công thức này, ta xét đặc thù của hình chóp mà đề bài cho. Nếu hình chóp có hai mặt bên cùng vuông góc với đáy và chiều cao của khối chóp chính là giao tuyến của hai mặt đó, ta vận dụng chiêu thức này .
Để xác lập đường cao của hình chóp, ta vận dụng định lý sau đây :

Ta cùng xét ví dụ minh họa sau đây để hiểu hơn về cách tính thể tích khối chóp này .
Ví dụ : Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BA = 3 a, BC = 4 a ; mặt phẳng ( SBC ) vuông góc với mặt phẳng ( ABC ). Biết SB = 2 a √ 3 và ∠ ( SBC ) = 30 º, tính thể tích khối chóp S.ABC.

2.2. Phương pháp tính thể tích khối chóp có cạnh bên vuông góc đáy

Phương pháp giải :
Ta có công thức thể tích khối chóp là $ V = \ frac { 1 } { 3 } \ frac { 1 } { 3 } S.h $ với S là diện tích quy hoạnh đáy, h là chiều cao. Khối chóp có cạnh bên vuông góc với đáy suy ra cạnh bên vuông góc với đáy là đường cao của chóp hay h = độ dài cạnh bên vuông góc với đáy .
Ví dụ minh họa : Cho khối chóp S.ABC có SA vuông góc với đáy, SA = 4 ; AB = 6 ; BC = 10 và CA = 8. Tính thể tích khối chóp S.ABC.
A. V = 40
B. V = 96
C. V = 32
D. V = 64
Giải :

2.3. Thể tích khối chóp s abcd có đáy là hình vuông vắn

Đối với khối chóp abcd có đáy là hình vuông vắn, ta có ví dụ minh họa sau đây :
Ví dụ : Cho khối chóp S.ABCD có đáy là hình vuông vắn cạnh a, SA vuông góc với đấy và SC tạo với mp ( SAB ) một góc 30 độ. Tính thể tích khối chóp ?
Giải :

2.4. Tìm thể tích khối chóp lập phương

Đây là dạng khối chóp đặc biệt quan trọng vì những mặt của khối chóp đều là hình vuông vắn ( lập phương ). Vì vậy, giải pháp tính thể tích khối chóp lập phương rất đơn thuần : $ V = a. a. a = a ^ { 3 } a ^ { 3 } $ ( do những cạnh của hình lập phương đều có độ dài bằng nhau, một cách khác của công thức thể tích là s3, trong đó s là độ dài cạnh của hình lập phương )
Ví dụ minh họa :
Tính thể tích khối lập phương có độ dài đường chéo là 27 cm .
Giải :

2.5. Thể tích khối chóp lăng trụ tam giác đều

Nếu một hình học xuất hiện bên là hình bình hành, hai mặt đáy song song và bằng nhau thì đa giác đó là hình lăng trụ. Một hình lăng trụ có mặt dưới là một tam giác đều thì đó là hình lăng trụ tam giác đều .
Ta cùng xét ví dụ sau để tính thể tích khối chóp lăng trụ tam giác đều :
Ví dụ : Cho hình lăng trụ ABC.A ’ B’C ’ có đáy ABC là tam giác đều cạnh bằng a = 2 cm và chiều cao là h = 3 cm. Hãy tính thể tích hình lăng trụ này .
Giải :

Vì đáy là tam giác đều cạnh a nên diện tích quy hoạnh
USD S_ { ABC } = a ^ { 2 }. \ frac { \ sqrt { 3 } } { 4 } = 2 ^ { 2 }. \ frac { \ sqrt { 3 } } { 4 } = \ sqrt { 3 } ( m ^ { 2 } ) S_ { ABC } = a ^ { 2 }. \ frac { \ sqrt { 3 } } { 4 } = 2 ^ { 2 }. \ frac { \ sqrt { 3 } } { 4 } = \ sqrt { 3 } ( m ^ { 2 } ) USD
Khi này, thể tích là USD V = S_ { ABC }. h = \ sqrt { 3 }. 3 = 3 \ int \ sqrt { 3 } ( m ^ { 3 } ) S_ { ABC }. h = \ sqrt { 3 }. 3 = 3 \ int \ sqrt { 3 } ( m ^ { 3 } ) USD

>> Xem thêm: Công thức tính thể tích khối lăng trụ đứng tam giác đều

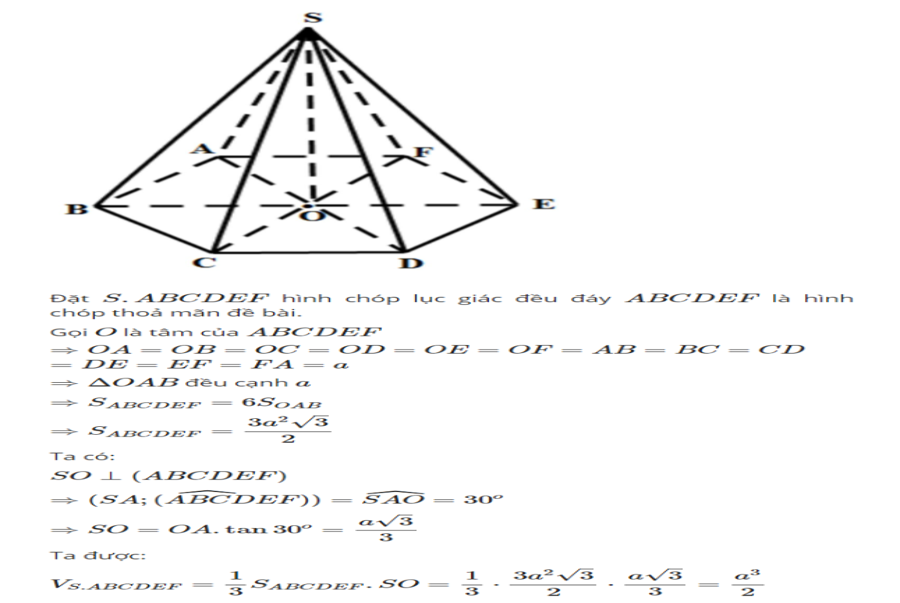
2.6. Cách tìm thể tích khối chóp lục giác đều

Cùng VUIHOC xét ví dụ minh họa sau đây về thể tích khối chóp lục giác đều .
Ví dụ : Một khối chóp lục giác đều, góc giữa cạnh bên và dưới mặt đáy là 30 độ, cạnh đáy a. Tính thể tích V của khối chóp ?
Giải :

2.7. Công thức tính thể tích khối chóp lăng trụ

Công thức tính thể tích lăng trụ : Khối lăng trụ có diện tích quy hoạnh đáy B và chiều cao h có thể tích được tính theo công thức : V = B.h

2.8. Tính thể tích khối chóp khi biết 3 cạnh bên

Đây là dạng đặc biệt quan trọng trong những bài toán tính thể tích khối chóp. Khi gặp trường hợp này, những em sử dụng công thức tổng quát sau :
Ta có BC = a, CA = b, AB = c, AD = d, BD = e, CD = f thuộc khối tứ diện ABCD, công thức tính thể tích của tứ diện 6 cạnh như sau :
V = 12M + N + P + Q., trong đó :

Ví dụ minh họa : Cho khối tứ diện ABCD có AB = CD = 8, AD = BC = 5 và AC = BD = 7. Thể tích khối tứ diện đã cho bằng bao nhiêu ?

2.9. Tìm thể tích khối chóp những cạnh đôi một vuông góc

Ta xét ví dụ minh họa sau đây để hiểu hơn cách tính thể tích khối chóp trong trường hợp khối chóp có những cạnh đôi một vuông góc như sau :
Cho tứ diện SABC có những cạnh SA, SB, SC đôi một vuông góc với nhau. Biết SA = 3 a, SB = 4 a, SC = 5 a. Tính theo a thể tích V của khối tứ diện SABC .
Giải :

2.10. Thể tích khối chóp tròn xoay

Ta hoàn toàn có thể dễ thấy, thể tích khối chóp tròn xoay tương tự như như công thức tính thể tích khối chóp :
USD V = \ frac { 1 } { 3 } Bh = \ frac { 1 } { 3 } \ pi r ^ { 2 } h \ frac { 1 } { 3 } Bh = \ frac { 1 } { 3 } \ pi r ^ { 2 } h USD
Trong công thức trên B là diện tích quy hoạnh đáy hình nón, r là nửa đường kính đáy hình nón, h là chiều cao của hình nón .
Cùng VUIHOC xét ví dụ minh họa sau đây tính thể tích khối chóp tròn xoay :

​​​​​​

>> Xem thêm: Công thức tính thể tích khối tròn xoay chính xác nhất

2.11. Tính thể tích của khối chóp tam giác đều

Đây là dạng toán đặc biệt quan trọng, thường Open trong những câu hỏi kiếm điểm 8 +. Các em cùng xét ví dụ minh họa sau đây để hiểu cách giải dạng bài tính thể tích khối chóp này :
Tính thể tích V của khối chóp tam giác đều SABC biết chiều cao hình chóp bằng h, góc SBA = a
Giải :

2.12. Công thức tính thể tích khối chóp tứ giác đều cạnh đáy bằng a

Cùng VUIHOC giải bài tập tính thể tích khối chóp tứ giác đều cạnh đáy bằng a với bài tập minh họa sau :
Tính thể tích khối chóp tứ giác đều V có toàn bộ những cạnh bằng a .
Giải :

Để ôn tập kỹ và thành thạo hơn 12 công thức tính thể tích khối chóp cũng như vận dụng tính thể tích khối chóp nâng cao, VUIHOC gửi Tặng những em học viên file tổng hợp bài tập rèn luyện tinh lọc. Các em nhớ lưu về để làm tài liệu ôn thi nhé !
VUIHOC đã cùng những em học viên ôn tập lại kim chỉ nan chung về thể tích khối chóp và 12 công thức thường gặp nhất trong những đề thi. Hy vọng rằng sau bài viết này, những em sẽ không gặp nhiều khó khăn vất vả trong quy trình ôn tập và giải toán thể tích khối chóp. Để học được nhiều những kiến thức và kỹ năng hay và cách cách giải mê hoặc ôn luyện thi trung học phổ thông, truy vấn ngay vuihoc.vn và ĐK khóa học ôn thi cấp tốc trung học phổ thông dành riêng cho sĩ tử 2004 nhé !

>> Xem thêm:

Source: http://139.180.218.5
Category: tản mạn