‍I. ĐỊNH NGHĨA ĐƯỜNG CAO TRONG TAM GIÁC

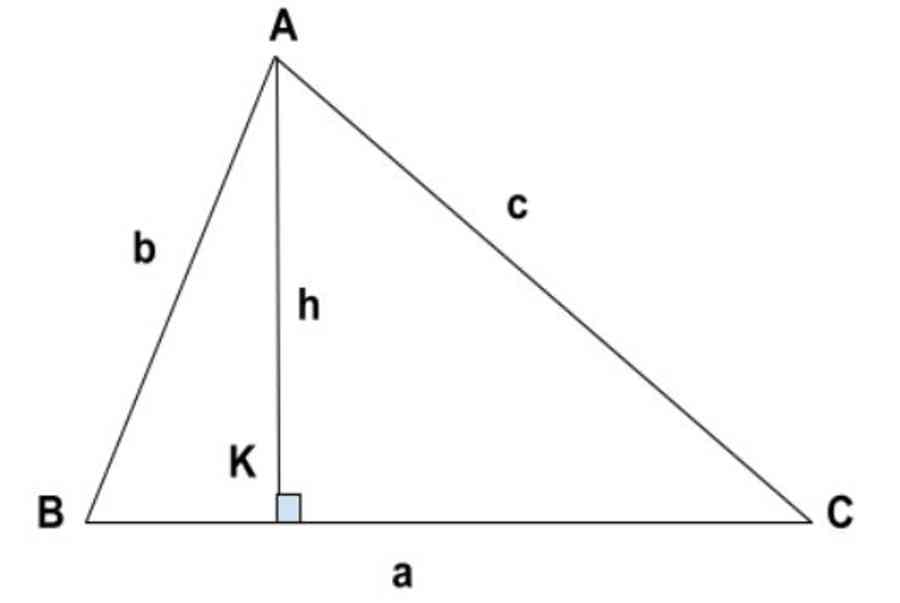
Đường cao trong tam giác là đường thẳng từ đỉnh tam giác hạ vuông góc xuống cạnh đối lập. Trong một tam giác có 3 đường cao và chúng đồng quy với nhau tại 1 điểm .Ví dụ : △ ABC trên có 3 đường cao được hạ từ 3 đỉnh A, B, C : AK, CQ, BN và chúng giao nhau tại O .

II. TÍNH CHẤT ĐƯỜNG CAO TRONG TAM GIÁC

Đường cao trong tam giác có tính chất:

Ba đường cao trong tam giác đồng quy với nhau tại 1 điểm, điểm đó gọi là trực tâm của tam giác.

Ví dụ : △ ABC trên có 3 đường cao AK, CQ, BN và chúng đồng quy tại O, O là trực tâm △ ABC .Chú ý : Không chỉ ở tam giác thường mà ở dạng tam giác vuông, tam giác cân, tam giác đều cũng có đường cao và đặc thù của đường cao vẫn giữ nguyên .

Đường cao trong tam giác vuông

Đối với tam giác vuông đường cao của tam giác có đặc thù là :Trong một tam giác vuông, đường cao của tam giác là hai cạnh bên góc vuông của tam giác đó và một đường cao hạ từ đỉnh góc vuông, và 3 đường cao đồng quy tại chính đỉnh góc vuông đó .Ví dụ : △ ABC vuông tại B có 3 đường cao là AB, BC, BM chúng đồng quy tại B .

Đường cao trong tam giác cân, tam giác đều

Đường cao trong tam giác cân hạ từ đỉnh cân xuống cạnh đáy vừa là đường trung tuyến, đường trung trực, đường phân giác .Đường cao trong tam giác đều hạ 3 đỉnh đều là đường trung tuyến, đường trung trực, đường phân giác .

III. CÔNG THỨC ĐỘ DÀI CỦA ĐƯỜNG CAO 

Có 5 cách tính độ dài đường cao của một tam giác

Công thức chung:

Công thức tính độ dài đường cao của một tam giác bằng diện tích quy hoạnh tam giác nhân 2 rồi chia cho cạnh đáy tương ứng với chiều cao đó :

$$h = {S \over a}$$

Trong đó :

• S: Diện tích của hình tam giác.

• a: Cạnh đáy tương ứng với chiều cao của hình tam giác.

• h: Chiều cao của tam giác.

Công thức tính độ dài đường cao của một tam giác ta hoàn toàn có thể sử dụng công thức Heron đã được chứng tỏ :USD USD h_a = 2. { \ sqrt { p. ( p – a ). ( p-b ). ( p-c ) } \ over a } $ $Trong đó :

• h: Chiều cao của tam giác.
• b. c: Độ dài các cạnh của hình tam giác.
• a: Cạnh đáy tương ứng với chiều cao của hình tam giác
• p: Nửa chu vi của hình tam giác.

Đường cao trong tam giác đều

Đường cao tam giác đều có độ dài bằng nhau, áp dụng định lý Heron ta có công thức tính đường cao trong tam giác đều:

$$h = {a \sqrt3\over 2}$$

Trong đó :

• h: Chiều cao của tam giác đều.

• a: Cạnh của tam giác đều.

Đường cao trong tam giác cân

Áp dụng công thức Pitago trong tam giác ta có công thức tính đường cao trong tam giác cân là :

$$h^2 = {a^2 }-{b^2\over 4}$$

Trong đó :

• h: Chiều cao của tam giác cân.
• a: Cạnh của tam giác cân.
• b: Cạnh đáy tương ứng với chiều cao từ đỉnh của hình tam giác cân.

Đường cao trong tam giác vuông

Áp dụng công thức tính cạnh và đường cao trong tam giác vuông, ta có công thức tính đường cao trong tam giác vuông là :

\(a^2 = {b^2 + c^2}\)
\(b^2 = {a.b’}\) và \(c^2 = {a.c’}\)
\(a.h = {b.c}\)
\(h^2= {b’.c’}\)
\({1\over h^2} = {1\over b^2} + {1\over c^2}\)

Trong đó :

• a, b, c: độ dài các cạnh của tam giác vuông.
• b’: đường chiếu của cạnh b ứng trên cạnh huyền.
• c’: đường chiếu của cạnh c ứng trên cạnh huyền.
• h: đường cao hạ từ đỉnh góc vuông.

IV. BÀI TẬP MINH HỌA VỀ CÔNG THỨC ĐỘ DÀI CỦA ĐƯỜNG CAO

Ví dụ: Cho hình △ABC vuông tại A có đường cao AH (H ∊ BC), biết BH= 9m, BC= 25m. Tính độ dài các đường cao trong △ABC?

Lời giải tham khảo:

H ∊ BC mà BH = 9 m, BC = 25 m⇒ CH = 25 – 9 = 16 ( m )Áp dụng công thức tính cạnh và đường cao trong tam giác vuông ta có :* ) AH² = BH x CH = 9 x 16 = 144⇒ AH = 12 ( m )* ) AB² = BC x BH = 25 x 9 = 225

⇒ AB = 15 (m)

* ) AC² = BC x CH = 25 x 16 = 400⇒ AC = 20 ( m )

Vậy độ dài 3 đường cao trong △ABC vuông tại A: AB, AC, AH lần lượt là 15m, 20m, 12m.

Source: http://139.180.218.5
Category: tản mạn