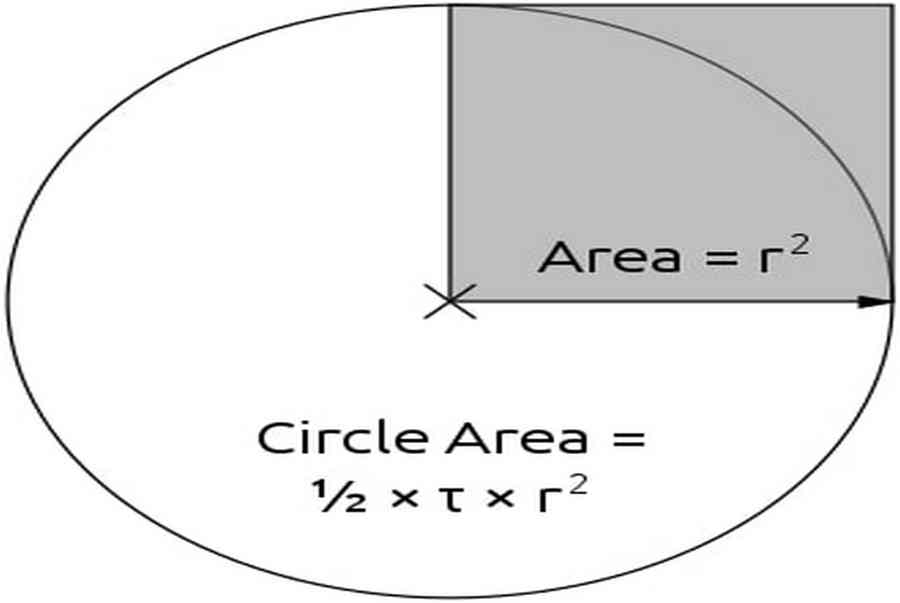
Ở lĩnh vực toán học, pi được xem là một hằng số vô tận và nó được áp dụng ở rất nhiều công thức khác nhau. Nhưng số pi không đơn giản chỉ là một hằng số mà nó còn có ý nghĩa quan trọng, nhiều vai trò quan trọng cùng sự tiến hóa về cách sử dụng theo thời gian. Bài viết sẽ cung cấp thông tin về khái niệm số pi cùng những đặc điểm cơ bản cần quan tâm.
Nội dung chính
1. Định nghĩa
Số pi có ký hiệu là π, còn có một cách gọi khác là hằng số Archimedes, đây là dãy số trong toán học mang trị gia bằng với phép chia chu vi đường tròn cùng đường kính của nó. Giá trị của dãy số này gần bằng 3,14. Nó được thể hiện qua chữ Hy Lạp kể từ khoảng thế kỷ XVIII.
Pi là dãy số vô tỉ, tức là nó không thể phản ánh được một cách cụ thể qua một tỷ số từ hai số nguyên. Hay có thể nói rằng đây là một hằng số thập phân vô hạn không tuần hoàn. Ngoài ra, pi còn là dãy số toàn năng, nghĩa là nó không thể trở thành nghiệm từ mọi đa thức ở hệ số hữu tỉ. Những ký tự thuộc phản ánh thập phân từ pi hiện ra theo một thứ tự bất kỳ, tuy là người ta vẫn chưa có thể xác thực được thông tin nào với tính ngẫu nhiên đó.
Trải qua một chặng đường hàng ngàn năm, những nhà toán học đã cố gắng đào sâu hơn để hiểu kỹ hơn về số pi, có thể là xác định giá trị của π cùng mức độ chính xác mỗi lúc một đúng. Ở trước thế kỷ 15, nhà toán học Archimedes cùng nhiều người khác đã dùng những phương pháp hình học, dựa vào đa giác nhằm tính toán đo lường trị số π.
Bạn đang đọc: Số pi là gì và các thông tin cơ bản về số pi cần biết
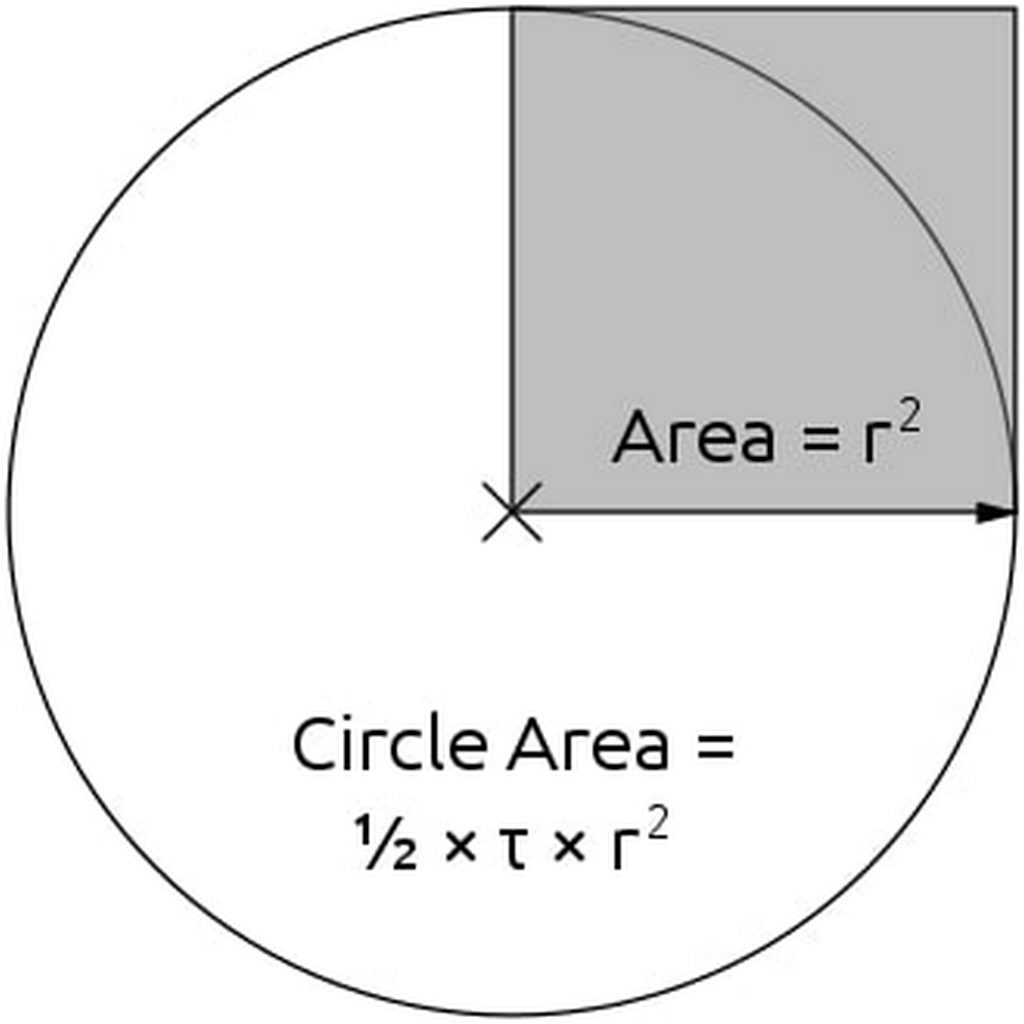Định nghĩa số pi
2. Tên gọi của Pi:
Những nhà toán học sử dụng một ký hiệu nhằm thể hiện được giá trị tỷ số giữa chu vi cũng như đường kính của hình tròn, ký hiệu này là π. Đây là ký tự được phản ánh thông qua tiếng Latin đọc là Pi. Sẽ dễ gây hiểu lầm giữa ký hiệu viết thường π cùng với ký tự được viết in hoa lên là Π, ký hiệu in hoa này trong toán học thể hiện cho tích một dãy số hoặc dãy hàm.
Nhà toán học sử dụng ký hiệu pi trong lần đầu tiên cùng cách hiểu như vậy là William Jones trong năm 1706 qua cuốn sách Nhập môn học toán của mình. Cụ thể thì ký hiệu π được xuất hiện lần đầu tiên ở khái niệm về 1/2 Periphery (π) ở một khúc nói về đường tròn mà đường kính là 1. Có khả năng ông chọn pi do nó là ký tự thứ nhất ở việc ký âm của ngôn ngữ Hy Lạp. Jones đã đề cập những phương trình từ π đúc kết qua bản viết có sẵn từ thiên tài John Machin, điều này làm cho nhiều người nghi ngờ rằng Machin có khả năng dùng ký tự π trước ông Jones, nhưng không có một chứng cứ cụ thể cho việc này. Bên cạnh đó, cách viết π đã hiện diện trong thời gian trước ở những ký tự hình học.
Sau thời điểm Jones đưa ra các viết của pi ở năm 1706, lúc đó chưa được chấp thuận bởi những nhà toán học còn lại, họ hay sử dụng ký tự c hay p. Việc này dần thay đổi khi Euler sử dụng ký hiệu này của pi ở năm 1736. Do Euler hay giao tiếp qua thư tay với những nhà toán học khắp Châu Âu, do đó mà ký tự này được lan rộng ra nhanh chóng. Ở năm 1748, Euler dùng pi ở một cuốn sách nổi tiếng của ông, tên là dẫn nhập giải tích vô hạn. Ông có đề cập đến việc sử dụng ký tự π để rút ngắn, ký hiệu này của pi sẽ là một nửa chu vi đường tròn mà bán kính của nó là 1, từ đó mà pi trở thành một ký hiệu được sử dụng phổ biến ở Châu Âu.
3. Tính chất của pi:
pi là một hằng số vô tỉ, tức là không thể biểu diễn hằng số này dưới hình thức tỉ số của hai số nguyên ví dụ nhua 22/7 hoặc một vài cách tính khác được thể hiện dưới hình thức là pi. Do pi là một hằng số vô tỉ, những chữ số trong số thập phân của nó là vô hạn và nó không phải là dạng tuần hoàn vô hạn những chữ số.
Có nhiều phương thức thể hiện số pi là dãy số vô tỉ cách tính dễ dàng nhất là sử dụng cách tính vi phân và cách thức chứng minh qua phản chứng. Số xấp xỉ của pi thông qua số hữu tỉ chưa được đo lường một cách cụ thể. Người ta tính toán rằng mức độ vô tỉ của pi cao hơn e hay in(2), tuy nhiên bé hơn số Liouville.
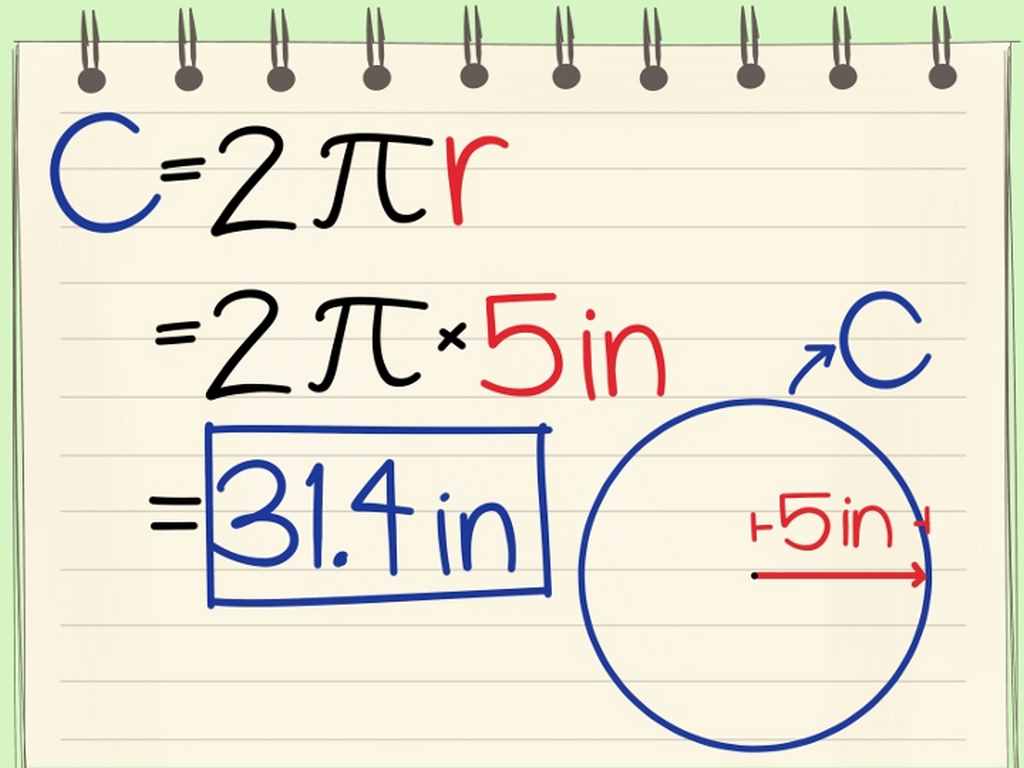Tính chất số Pi
Tiếp theo là do chưa có một dãy số toàn năng hoàn toàn có thể được giám sát trải qua dựng hình với thước kẻ hay compa do đó mà bài toán cầu phương hình tròn trụ khó hoàn toàn có thể giải được. Hiểu theo nghĩa khác thì khi chỉ dùng compa hay thước kẻ thì khó hoàn toàn có thể tạo ra một hình vuông vắn mà có diện tích quy hoạnh ngang bằng với diện tích quy hoạnh hình tròn trụ có sẵn. Cầu phương hình tròn trụ là một trong số những dạng toán hình học có tiếng tăm ở thời trước. Một vài nhà toán học không chuyên ở thời gian lúc bấy giờ đã từng nói rằng họ thành công xuất sắc tuy điều này khó hoàn toàn có thể xảy ra .
4. Việc sử dụng số Pi đã tiến hóa theo thời gian.
Từ thế kỷ 17 trở về trước, số pi được sử dụng ở những dạng toán về hình tròn như đã nói ở phía trên cho các mối liên kết giữa số pi và hình tròn.
Mãi đến thế kỷ 17, người ta còn thấy số pi được sử dụng nhằm xác định diện tích cũng như chu vi của những đường cong khác như chiều dài cung tròn (arc), hypocycloid ( hình cong được tạo ra thông qua một điểm nằm cố định ở đường tròn nhỏ khi đặt nó xoay quanh một đường tròn khác mà bán kính lớn hơn gấp nhiều lần). Mãi đến thế kỷ 20, pi được dùng ở đa lĩnh vực ví dụ như sản xuất hay các khía cạnh về toán học.
Pi còn được sử dụng nhằm đo lường chu vi trái đất. Mặc dù là việc đo lường giá trị hằng số này không dễ dàng tuy nhiên đây được xem là hằng số cực kỳ hiệu quả ở những cách đo lường cần sử dụng nó. Ví dụ như bạn làm tròn pi lên khoảng 9 số sau dấu phẩy và sử dụng để đo lường chu vi trái đất, kết quả đem lại sẽ rất đúng. Cho từng 40.000 km, số pi chỉ chênh lệch khoảng 0.62cm. Khi bạn thích toán học, bạn sẽ thấy yếu tố này tốt như thế nào.
Sự tiến hóa trong việc dùng số pi
5. Lịch sử số pi
Số pi đã có mặt từ khoảng 4000 năm trước và tạo ra thông qua người Babylon cổ đại. Có tài liệu từ xa xưa đâu đó khoảng năm 1900 đến 1680 trước công nguyên đã phát hiện pi bằng 3,125. Người Ai Cập cổ xưa đã tìm thấy điều như vậy, như là cách xác minh những gì được nếu bởi Rhind ở những năm 1650 trước Công nguyên. Trong đó, người Ai Cập đo lường được dịch tích hình tròn qua công thức mà số pi gần bằng với 3,1605. Ngay cả ở kinh thánh cũng có nhắc đến ký hiệu toán học pi đo lường gần đúng.
Zu Chongzi tại Trung Quốc đã đo lường được số pi bằng với 355/113, tuy là việc ông có được kết quả này ra sao thì vẫn chưa có lời giải, do tài liệu của ông đã thất lạc.
Lời kết
Và đó là các thông tin cơ bản về số pi mà bạn cần quan tâm. Có thể thấy bên cạnh lĩnh vực toán học thì nó còn được sử dụng ở nhiều khía cạnh trong cuộc sống. Số pi dù trở thành một yếu tố quen thuộc trong những công thức toán nhưng không phải ai cũng biết được ý nghĩa sâu xa và lịch sử của nó.
Source: http://139.180.218.5
Category: Thuật ngữ đời thường