Tam giác vuông là gì?

Tam giác vuông là một tam giác có một góc là góc vuông bằng góc 90 độ .
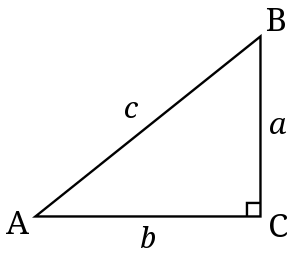
Ví dụ : Tam giác Ngân Hàng Á Châu vuông tại C :

Cạnh AB đối diện với góc vuông gọi là cạnh huyền.

Hai cạnh AC và CB kề với góc vuông gọi là cạnh bên ( hay còn gọi là cạnh góc vuông )

Tính chất của tam giác vuông

Trong một tam giác vuông có :

• Hai góc nhọn phụ nhau.
• Bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
• Đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
• Mỗi cạnh của tam giác vuông là trung bình nhân của cạnh huyền và hai đoạn của cạnh huyền kề với cạnh bên.

Tham khảo thêm:

Dấu hiệu nhận biết tam giác vuông

• Tam giác có 1 góc vuông là tam giác vuông
• Tam giác có 2 góc nhọn phụ nhau là tam giác vuông
• Tam giác có bình phương độ dài 1 cạnh bằng tổng bình phương độ dài 2 cạnh kia là tam giác vuông (định lý Pytago đảo)
• Tam giác có đường trung tuyến ứng với 1 cạnh bằng nửa cạnh ấy là tam giác vuông
• Tam giác nội tiếp đường tròn có 1 cạnh là đường kính thì tam giác đó vuông
• Tam giác có cạnh đối diện góc 30° bằng một nửa một cạnh khác trong tam giác thì tam giác đó vuông.

Cách chứng minh tam giác vuông

Cách 1: Chứng minh tam giác đó có 2 góc nhọn phụ nhau.

Ví dụ : Tam giác OAB có Góc A + B = 90 °
=> Tam giác OAB vuông tại O

Cách 2: Chứng minh tam giác đó có bình phương độ dài 1 cạnh bằng tổng bình phương độ dài 2 cạnh kia.

Ví dụ : Tam giác OAB có OA2 + OB2 = AB2
=> Tam giác OAB vuông tại O

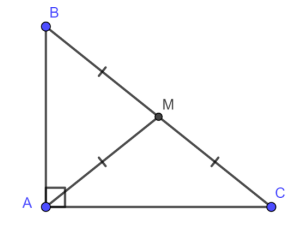
Cách 3: Chứng minh tam giác đó có đường trung tuyến ứng với 1 cạnh bằng nửa cạnh ấy.

Ví dụ : Tam giác OAB có M là trung điểm AB, biết MO = MA = MB = ½ AB
=> Tam giác OAB vuông tại O

Cách 4: Chứng minh tam giác đó nội tiếp đường tròn và có 1 cạnh là đường kính.

Ví dụ : Tam giác OAB nội tiếp đường tròn đường kính AB
=> Tam giác OAB vuông tại O

Bài tập về tam giác vuông có lời giải

Ví dụ 1 : Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Kẻ AM là đường trung tuyến của tam giác ABC .
a. Chứng minh tam giác ABC là tam giác vuông .
b. Tính độ dài đường trung tuyến AM ?

Lời giải
a. Ta có : AB2 + AC2 = 62 + 82 = 100 = BC2
Suy ra, tam giác ABC vuông tại A
b. Vì AM là đường trung tuyến ứng với cạnh huyền BC nên :
AM = ½BC = 10 : 2 = 5 cm
Ví dụ 2 : Cho tam giác ABC có AB = 15 cm, BC = 8 cm, AC = 17 cm

a. Chứng minh tam giác ABC là tam giác vuông

b. Trên tia đối của tia BC lấy điểm D sao cho BD = 8 cm. Tính độ dài AD và chứng tỏ AD = AC
Lời giải
Vì AC = 17 cm nên AC là cạnh lớn nhất mà đối lập với cạnh AC là góc B

Ta có :
AC2 = 172 = 289 (1)

AB2 + BC2 = 152 + 82 = 289 ( 2 )
Từ ( 1 ) và ( 2 ) => AC2 = AB2 + BC2 => ΔABC vuông tại B
b ) Áp dụng định lí pytago trong Δ vuông ABD, ta có :
AD2 = AB2 + BD2 = 152 + 82 = 289
=> AD = √ 289 = 17 cm ( 3 )
Mà AC = 17 cm ( 4 )
Từ ( 3 ), ( 4 ) => AD = AC
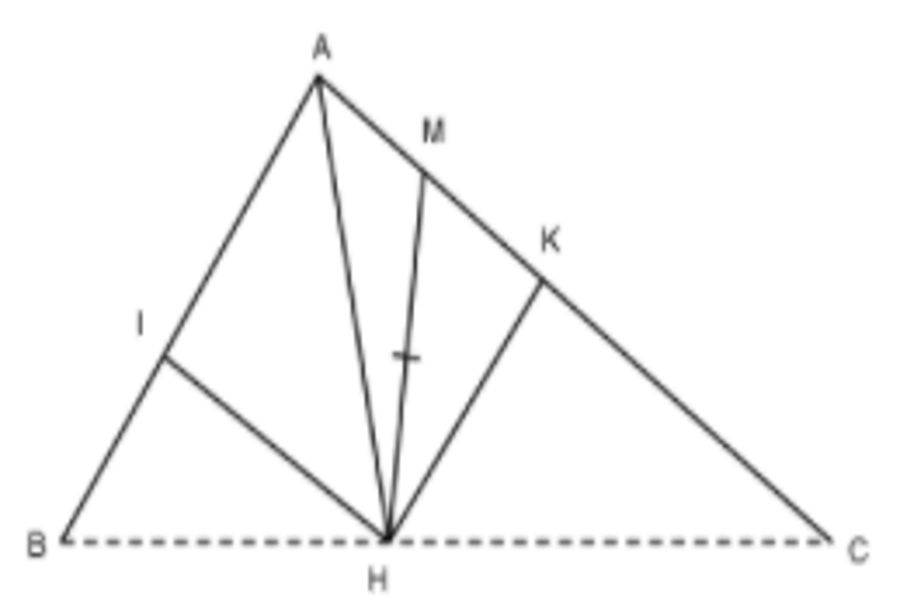
Ví dụ 3 : Cho tam giác ABC vuông tại A ( AB < AC ), M là một điểm thuộc cạnh AC. Kẻ MH vuông góc với BC ( H ∈ BC ). Biết MH = HB. Chứng minh rằng AH là tia phân giác của góc A

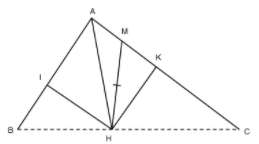
Lời giải

Suy ra góc A1 = góc A1
Vậy AH là tia phân giác của góc A
Hy vọng với triết lý về định nghĩa, tín hiệu phân biệt và đặc thù tam giác vuông hoàn toàn có thể giúp bạn vận dụng vào làm những bài tập chứng tỏ tam giác vuông đơn thuần nhé

5/5 – ( 2 bầu chọn )

Source: http://139.180.218.5
Category: tản mạn