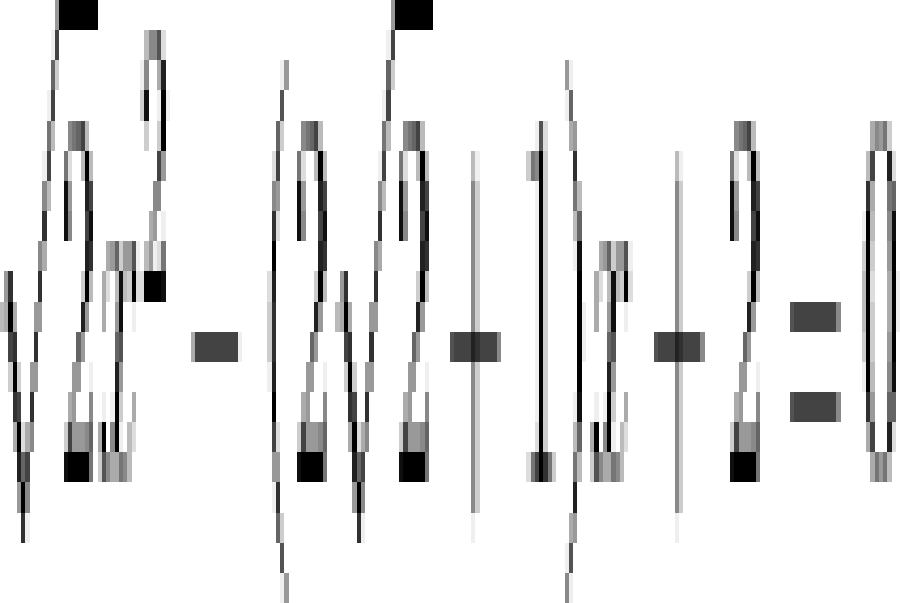Nội dung chính
1. Cơ sở tính nhẩm
Cơ sở tính nhẩm xuất phát từ định lí Vi-ét quen thuộc sau : 2
Định lí Vi-ét
Định lý gồm 2 phần, thuận và đảo:
* Nếu phương trình trình
có hai nghiệm
thì
* Ngược lại, nếu hai số
và
có tổng
và tích
thì và là các nghiệm của phương trình
2. Các dạng tính nhẩm thường gặp
Từ phần hòn đảo, thuận tiện suy ra các tác dụng sau .
Loại 1: a = 1, b = tổng, c = tích
* Nếu phương trình có dạng ![]() thì phương trình đó có hai nhiệm và .
thì phương trình đó có hai nhiệm và .
* Nếu phương trình có dạng ![]() thì phương trình có hai nghiệm
thì phương trình có hai nghiệm ![]() và
và ![]()
Tóm lại :
![]()
![]()
Như vậy, với loại này bạn cần thực hiện 2 phép nhẩm: “Phân tích hệ số ![]() thành tích và
thành tích và ![]() thành tổng”. Trong hai phép nhẩm đó, bạn nên nhẩm hệ số trước rồi kết hợp với để tìm ra hai số thỏa mãn tích bằng và tổng bằng .
thành tổng”. Trong hai phép nhẩm đó, bạn nên nhẩm hệ số trước rồi kết hợp với để tìm ra hai số thỏa mãn tích bằng và tổng bằng .
Khi triển khai, bạn nhẩm trong đầu như sau :
Tích của hai nghiệm bằng, mà tổng lại bằng
Ví dụ phương trình
* ![]()
Nhẩm: “Tích của hai nghiệm bằng 6, mà tổng lại bằng 5”. Hai số đó là: 2 và 3 vì 6 = 2.3 và 5 = 2 + 3. Vậy phương trình có hai nghiệm ![]()
* ![]()
Nhẩm: “Tích của hai nghiệm bằng 10, mà tổng lại bằng 7”. Hai số đó là: 2 và 5 vì 10 = 2.5 và 7 = 2 + 5. Vậy phương trình có hai nghiệm ![]()
Loại 2: a + b + c = 0 và a – b + c = 0
* Nếu thay ![]() vào (1) thì bạn sẽ có trường hợp nhẩm nghiệm quen thuộc
vào (1) thì bạn sẽ có trường hợp nhẩm nghiệm quen thuộc ![]() , với
, với ![]() .
.
* Nếu thay ![]() vào (1) thì bạn sẽ có trường hợp nhẩm nghiệm
vào (1) thì bạn sẽ có trường hợp nhẩm nghiệm ![]() , với
, với ![]() .
.
Do loại này đã quá quen thuộc với bạn, nên bài viết không xét các ví dụ cho trường hợp này mà tập trung chuyên sâu vào loại 1 và loại 3 .
Loại 3: Hai nghiệm là nghịch đảo của nhau
Nếu ![]() và
và ![]() thì phương trình (1) có dạng
thì phương trình (1) có dạng
![]()
khi đó phương trình có hai nghiệm là nghịch đảo của nhau ![]() . Đây cũng là trường hợp hay gặp khi giải toán. Ví dụ phương trình
. Đây cũng là trường hợp hay gặp khi giải toán. Ví dụ phương trình
* ![]() có hai nghiệm
có hai nghiệm ![]()
* ![]() có hai nghiệm
có hai nghiệm ![]()
Loại 4: Những trường hợp còn lại
Với một phương trình có hệ số ![]() mà không phải loại 2, loại 3 thì bạn nên chia cả hai vế cho
mà không phải loại 2, loại 3 thì bạn nên chia cả hai vế cho ![]() , quy về loại 1 để nhẩm. Còn nếu vẫn không nhẩm được thì bạn biết phải làm gì rồi chứ 😀3
, quy về loại 1 để nhẩm. Còn nếu vẫn không nhẩm được thì bạn biết phải làm gì rồi chứ 😀3
3. Một số ví dụ vận dụng
Ví dụ 1. Phương trình
* ![]() có hai nghiệm
có hai nghiệm ![]() vì 12 = 2.6 và 8 = 2 + 6
vì 12 = 2.6 và 8 = 2 + 6
* ![]() có hai nghiệm
có hai nghiệm ![]() vì 12 = 3.4 và 7 = 3 + 4
vì 12 = 3.4 và 7 = 3 + 4
* ![]() có hai nghiệm
có hai nghiệm ![]() vì -12 = (-3).4 và 1 = (-3) + 4
vì -12 = (-3).4 và 1 = (-3) + 4
* ![]() có hai nghiệm
có hai nghiệm ![]() vì -12 = 3.(-4) và -1 = 3 + (-4)
vì -12 = 3.(-4) và -1 = 3 + (-4)
* ![]() có hai nghiệm
có hai nghiệm ![]() vì -12 = (-2).6 và 4 = (-2) + 6
vì -12 = (-2).6 và 4 = (-2) + 6
* ![]() có hai nghiệm
có hai nghiệm ![]() vì -12 = 2.(-6) và -4 = 2 + (-6)
vì -12 = 2.(-6) và -4 = 2 + (-6)
Ví dụ 2. Phương trình
* ![]() 4 có hai nghiệm
4 có hai nghiệm ![]() , vì nó có dạng
, vì nó có dạng
![]()
* ![]() có hai nghiệm
có hai nghiệm ![]() , vì nó có dạng
, vì nó có dạng
![]()
* ![]() có hai nghiệm
có hai nghiệm ![]() , vì nó có dạng
, vì nó có dạng
![]()
Ví dụ 3. Phương trình
* ![]() có hai nghiệm
có hai nghiệm ![]() 5
5
* ![]() có hai nghiệm
có hai nghiệm ![]() 6
6
* ![]() 7
7
4. Bình luận
Khi mới làm quen với tính nhẩm, có thể bạn sẽ gặp một chút khó khăn, nhưng đừng vì thế mà ngại khó và bỏ cuộc. Hãy tưởng tượng thành quả mà tính nhẩm đem lại cho bạn là “không đếm được” so với những “trở ngại đếm được” mà bạn đang phải đối mặt. Bạn sẽ có thêm động lực tiến lên.
| “ | Đừng cảm thấy tiếc vì bụi hoa hồng có gai mà hãy vui vì trong bụi gai có hoa hồng. | ” |
| — Abraham Lincoln |

Thapsang.vn để nhận được thông báo khi có cập nhật mới.Mời bạn đón đọc các bài viết tiếp theo bằng cách đăng kí nhận bài viết mới qua email hoặc like fanpageđể nhận được thông tin khi có update mới .
Source: http://139.180.218.5
Category: tản mạn